Efficient load aware routing scheme

IEEE TRANSACTIONS ON MOBILE COMPUTING, VOL. 9, NO. 9, SEPTEMBER 2010 1293

Efficient Load-Aware Routing Scheme
for Wireless Mesh Networks
Kae Won Choi, Wha Sook Jeon, Senior Member, IEEE, and Dong Geun Jeong, Senior Member, IEEE

Abstract—This paper proposes a load-aware routing scheme for wireless mesh networks (WMNs). In a WMN, the traffic load tends to
be unevenly distributed over the network. In this situation, the load-aware routing scheme can balance the load, and consequently,
enhance the overall network capacity. We design a routing scheme which maximizes the utility, i.e., the degree of user satisfaction, by
using the dual decomposition method. The structure of this method makes it possible to implement the proposed routing scheme in a
fully distributed way. With the proposed scheme, a WMN is divided into multiple clusters for load control. A cluster head estimates
traffic load in its cluster. As the estimated load gets higher, the cluster head increases the routing metrics of the routes passing through
the cluster. Based on the routing metrics, user traffic takes a detour to avoid overloaded areas, and as a result, the WMN achieves
global load balancing. We present the numerical results showing that the proposed scheme effectively balances the traffic load and
outperforms the routing algorithm using the expected transmission time (ETT) as a routing metric.

Index Terms—Wireless mesh network, load-aware routing, utility, dual decomposition.

Ç

1 INTRODUCTION

A wireless mesh network (WMN) consists of a number
of wireless routers, which do not only operate as hosts
but also forward packets on behalf of other routers. WMNs
over the traditional hop-count routing metric, they neglect
the problem of traffic load imbalance in the WMN.
In the WMN, a great portion of users intends to
have many advantages over conventional wired networks, communicate with outside networks via the wired gate-
such as low installation cost, wide coverage, and robust- ways. In such environment, the wireless links around the
ness, etc. Because of these advantages, WMNs have been gateways are likely to be a bottleneck of the network. If the
rapidly penetrating into the market with various applica- routing algorithm does not take account of the traffic load,
tions, for example, public Internet access, intelligent some gateways may be overloaded while the others may
transportation system (ITS), and public safety [1]. One of not. This load imbalance can be resolved by introducing a
the main research issues related to WMNs is to develop the load-aware routing scheme that adopts the routing metric
routing algorithm optimized for the WMN. with load factor. When the load-aware routing algorithm is
designed to maximize the system capacity, the major benefit
In mobile ad-hoc networks, the primary concern of
of the load-aware routing is the enhancement of the overall
routing has been robustness to high mobility. However,
system capacity due to the use of underutilized paths.
nodes in the WMN are generally quasi-static in their location. Although there have been some works on load-aware
Thus, the focus of the routing studies in the WMN has moved routing for mobile ad-hoc networks (e.g., [9], [10]) and
to performance enhancement by using sophisticated routing WMNs (e.g., [11], [12], [13]), they simply include some load
metrics [2], [3], [4], [5], [6], [7], [8]. For example, as the routing factors in the routing metric without consideration of the
metrics, researchers have proposed the expected transmis- system-wide performance.
sion number (ETX) [2], the expected transmission time (ETT) In this paper, we propose a load-aware routing scheme,
and weighted cumulative ETT (WCETT) [5], the metric of which maximizes the total utility of the users in the WMN.
interference and channel switching (MIC) [6], and the The utility is a value which quantifies how satisfied a user is
modified expected number of transmissions (mETX) and with the network. Since the degree of user satisfaction
depends on the network performance, the utility can be
effective number of transmissions (ENTs) [8]. Although these
given as a function of the user throughput. Generally, the
metrics have shown significant performance improvement
utility function is concave to reflect the law of diminishing
marginal utility. To design the scheme, we use the dual
. K.W. Choi is with the Department of Electrical and Computer Engineering, decomposition method for utility maximization [14], [16].
University of Manitoba, Room E2-390 EITC Building, 75A Chancellor’s Using this method, we can incorporate not only the load-
Circle, Winnipeg, MB R3T 5V6, Canada. E-mail: kaewon.choi@gmail.com. aware routing scheme but also congestion control and fair
. W.S. Jeon is with the School of Electrical Engineering and Computer rate allocation mechanisms into the WMN. Most notably,
Science, Seoul National University, Gwanak-gu, Seoul 151-742, Korea.
E-mail: wsjeon@snu.ac.kr. we can implement the load-aware routing scheme in a
. D.G. Jeong is with the School of Electronics and Information Engineering, distributed way owing to the structure of the dual
Hankuk University of Foreign Studies, Cheoin-gu, Yongin-si, Gyonggi-do decomposition method.
449-791, Korea. E-mail: dgjeong@hufs.ac.kr. In the proposed routing scheme, a WMN is divided into
Manuscript received 7 Apr. 2008; revised 22 Oct. 2008; accepted 15 Dec. multiple overlapping clusters. A cluster head takes role of
2009; published online 28 Apr. 2010. controlling the traffic load on the wireless links in its cluster.
For information on obtaining reprints of this article, please send e-mail to:
tmc@computer.org, and reference IEEECS Log Number TMC-2008-04-0129. The cluster head periodically estimates the total traffic load
Digital Object Identifier no. 10.1109/TMC.2010.85. on the cluster and increases the “link costs” of the links in the
1536-1233/10/$26.00 ß 2010 IEEE Published by the IEEE CS, CASS, ComSoc, IES, & SPS

1294 IEEE TRANSACTIONS ON MOBILE COMPUTING, VOL. 9, NO. 9, SEPTEMBER 2010

cluster, if the estimated load is too high. In this scheme, each (ROMER) algorithm in [20] also uses opportunistic for-
user chooses the route that has the minimum sum of the link warding to deal with short-term link quality variation. The
costs on it. Thus, a user can circumvent overloaded areas in ROMER maintains the long-term routes and opportunisti-
the network, and therefore, the network-wide load balance cally expands or shrinks them at runtime.
can be achieved. The works in [21] and [22] focus on the applications
The major advantages of the proposed load-aware accessing the wired gateways. The ad hoc on-demand
routing scheme can be summarized as follows: distance vector spanning tree (AODV-ST) in [21] is an
adaptation of the AODV protocol to the WMN with the
. Designed by the dual decomposition method, the wired gateways. The AODV-ST constructs a spanning tree of
proposed load-aware routing scheme maximizes the which the root is the gateway. In [22], the authors propose a
system-wide performance.
routing and channel assignment algorithm for the multi-
. The proposed scheme is scalable, has low control
channel WMN. In this algorithm, a spanning tree is formed in
and computation overheads, and can be easily
such a way that a node attaches itself to the parent node.
implemented by means of the existing ad hoc
The load-aware routing protocols [9], [10], [11], [12], [13]
routing protocols [17].
incorporate the load factor into their routing metrics. The
The remainder of the paper is organized as follows: In dynamic load-aware routing (DLAR) in [9] takes as the
Section 2, we briefly overview the related works. Section 3 routing metric the number of packets queued in the node
outlines the system model. In Section 4, we formulate the interface. The load-balanced ad hoc routing (LBAR) in [10]
optimization problem and solve it by using the dual counts the number of active paths on a node and its neighbors,
decomposition method. In Section 5, we explain how to and uses it as a routing metric. Both the DLAR and LBAR are
implement the proposed routing scheme in a distributed designed for the mobile ad hoc network, and aim to reduce
way. Section 6 presents the numerical results which show the packet delay and the packet loss ratio. In [11], an
the performance of the proposed scheme. Finally, the paper admission control and load balancing algorithm is proposed
is concluded with Section 7. for the 802.11 mesh networks. In this work, the available radio
time (ART) is calculated for each node, and the route with the
2 RELATED WORKS largest ART is selected when a new connection is requested.
This algorithm tries to maximize the average number of
For the WMN, a number of routing metrics and algorithms
connections. In [12], the authors propose the WCETT load
have been proposed to take advantage of the stationary
balancing (WCETT-LB) metric. The WCETT-LB is the
topology. The first routing metric is the ETX [2], which is the
expected number of transmissions required to deliver a WCETT augmented by the load factor consisting of the
packet to the neighbor. In [3], the authors propose the average queue length and the degree of traffic concentration.
minimum loss (ML) metric which is used to find the route The QoS-aware routing algorithm with congestion control
with lowest end-to-end loss probability. In [4], the medium and load balancing (QRCCLB) in [13] calculates the number
time metric (MTM) is proposed for the multirate network. of congested nodes on each route and chooses the route with
The MTM of a link is inverse proportional to the physical the smallest number of congested nodes.
layer transmission rate of the link. The ETT in [5] is a Compared to these load-aware routing protocols, the
proposed routing scheme has three major advantages. First,
combination of the ETX and the MTM. The ETT is a required
the proposed scheme is design to maximize the system
time to transmit a single packet over a link in the multirate
capacity by considering all necessary elements for load
network, calculated in consideration of both the number of
balancing, e.g., the interference between flows, the link
transmissions and the physical layer transmission rate. The
capacity, and the user demand, etc. On the other hand, the
authors in [5] also suggest the routing metric and algorithm existing protocols fail to reflect these elements since they use
for the multiradio WMN, which are the WCETT and the heuristically designed routing metrics. For example, the
multiradio link quality source routing (MR-LQSR), respec- DLAR, the ART, and the WCETT-LB do not take account of
tively. The WCETT is a modification of the ETT to consider the interference between flows. Also, the link capacity is not
the intraflow interference. While the WCETT only considers considered by the DLAR, the LBAR, the ART, and the
the intraflow interference, the MIC [6] and the interference QRCCLB. Second, the proposed scheme can guarantee
aware (iAWARE) [7] take account of the interflow inter- fairness between users. When the network load is high, it is
ference as well as the intraflow interference. of importance for users to fairly share scarce radio resources.
In [8], the mETX and the ENT are proposed to cope with However, the existing protocols cannot fairly allocate
the fast link quality variation. These routing metrics contain resources, since they are unable to distinguish which route
the standard deviation of the link quality in addition to the is monopolized by a small number of users. Third, the
average link quality. The blacklist-aided forwarding (BAF) proposed scheme can provide routes stable over time. Since
algorithm in [18] is proposed to tackle the problem of short- most of the existing protocols adopt highly variable routing
term link quality degradation by disseminating the black- metrics such as the queue length or the collision probability,
list, i.e., a set of currently degraded links. The ExOR they are prone to suffer from the route flapping problem.
algorithm in [19] decides the next hop after the transmis- We design the proposed routing scheme by using the
sion for that hop without predetermined routes. The ExOR dual decomposition method for the network utility max-
can choose the next hop that successfully received the imization. A brief introduction to this method can be found
packet, and therefore, it is robust to packet error and link in [14], [15], and an elaborate explanation and a number of
quality variation. The resilient opportunistic mesh routing examples can be found in [16]. To use this method, one

CHOI ET AL.: EFFICIENT LOAD-AWARE ROUTING SCHEME FOR WIRELESS MESH NETWORKS 1295

TABLE 1
Table of Symbols

Fig. 1. Example mesh network.

should formulate the global optimization problem that is to links in the network, respectively. In Table 1, we summarize
maximize the total system utility under the constraints on all mathematical notations introduced in this section.
the traffic flows and the radio resources. After the The WMN under consideration provides a connection-
constraints are relaxed by the Lagrange multipliers, the oriented service, where connections are managed in the unit
whole problem can be decomposed into the subproblems of a flow. A flow is also unidirectional. A user can
which are solved by the different network layers in the communicate with the other user or the gateway node after
different network nodes. In the decomposed problem, the setting up a flow connecting them. Since a user is connected
Lagrange multipliers act as a interface between the layers to a unique node, the flow between a pair of users can also
and the nodes, enabling the distributed entities to find the be specified by the corresponding node pair. The node
global optimal solution only by solving their own subpro- where a flow starts (ends) will be called the source
blems. Therefore, the dual decomposition method provides (destination) node of the flow. Fig. 1 shows an example
a systematical way to design a distributed algorithm which scenario where a user intends to send data to outside
finds the global optimal solution. networks. As seen in this figure, if a flow conveys data to
(from) outside networks, all gateway nodes can be the
destination (source) node of the flow. We will identify a
3 SYSTEM MODEL flow by an index, generally f, and define F as the set of the
3.1 Mesh Network Structure indices of all flows in the network.
Data traffic on a flow is conveyed to the destination node
Each wireless router in a WMN is fixed at a location. Thus, through a multihop route. We only consider acyclic routes.
the WMN topology does not change frequently and the Thus, a route can be determined by the set of all intermediate
channel quality is quasi-static. In addition, each wireless links that the route takes. We will index a route by r and
router serves so many subscribers (i.e., users) in general that define Dr as the set of the indices of all intermediate links on
the characteristic of the aggregated traffic is stable over time. the route r. For a flow, there can be a number of possible
Therefore, we design the routing scheme under the system routes that connect the source and destination nodes. Fig. 1
model of which topology and user configuration are stable. shows some of the possible routes that a flow can take to
In Fig. 1, we illustrate an example of the WMN. In this send data to the outside networks. Let Gf denote the set of
figure, a node stands for a wireless router, which not only the indices of all possible routes for flow f.
delivers data for its own users, but also relays data traffic for For mathematical development, we assume that a flow can
other wireless routers. Among nodes, there are some utilize multiple routes simultaneously by dividing its data
gateway nodes connected to the wired backhaul network. traffic into these routes. We limit the possible data rate of the
Each user is associated with its serving node. In this paper, traffic conveyed by a flow on each route to control the amount
we do not deal with the interface between a user and its of traffic injected to the WMN. Let f;r denote the “flow data
serving node to focus on the mesh network itself. Through rate” which is defined as the maximum data rate at which the
the serving node, a user can send (receive) data traffic to flow f can send data traffic on the route r. We also define
(from) the other user in the WMN or to (from) outside f :¼ ðf;r Þr2Gf as the “flow data rate vector” of flow f. The
networks via the gateway nodes. If node n can transmit data sum of all the components in a flow data rate vector is limited
to node m directly (i.e., without relaying), there exists a link to the “maximumP flow data rate,” denoted by max . That is, it
from the node n to the node m. In this paper, we define a link should hold that r2Gf f;r max .
as unidirectional. For the mathematical representation, we We will call f the “multipath flow data rate vector,” if
define N and L as the sets of the indices of all nodes and all f;r 0 for more than one r in Gf . On the other hand, we


will refer to f as the “single-path flow data rate vector,” if transmission. If two links are adjacent enough to interfere
f;
0 for only one “active route”
and f;r ¼ 0 for the with each other, packets cannot be conveyed through the
other rs in Gf . Since the multipath routing is hard to be two links at the same time. To incorporate this restriction
implemented in a practical sense, we will focus on finding into the proposed scheme, we divide the WMN into
the single-path flow data rate vectors for all flows in the multiple overlapping clusters. A cluster includes the links
WMN. Let
f denote the active route of the flow f that has adjacent enough to interfere with each other. Therefore, any
the single-path flow data rate vector. In case that all flows pair of links in the same cluster cannot deliver packets
simultaneously. A cluster is generally indexed by c, and let
have the single-path flow data rate vector, we can let
:¼

C be the set of the indices of all clusters in the WMN. We
ð
f Þf2F denote the “active route vector.”
also define Mc as the set of all links in the cluster c.
Deciding a single-path flow data rate vector is equivalent
The proposed scheme estimates the traffic load in each
to deciding an active route for the flow and the flow data
cluster. The traffic load in a cluster is the sum of the traffic
rate on the active route. An application using the flow can load on the links in the cluster. If the traffic load in a cluster is
send user data through the active route at its flow data rate. estimated to be too high, the proposed scheme can redirect
The active route can be decided in such a way that the the routes passing through the overloaded cluster for load
global load balancing is accomplished. In addition, network balancing. The airtime ratio of a link represents the traffic
congestion can be controlled and fairness can be guaranteed load on the link. If the sum of the airtime ratios of the links in
by deciding the flow data rate properly. Therefore, the load- a cluster exceeds a certain bound, the cluster can be regarded
aware routing, congestion, and fairness problems can be as overloaded.
solved at the same time, if we find a way to calculate Roughly, we assume that a fixed portion of the time can
appropriate flow data rate vectors. be used for data transmission, while the remainder is used
for the purpose of control, e.g., control message exchange
3.2 Physical and Medium Access Control Layer
and random back-off. Let

denote the ratio of the time for
Model
data transmission to the whole time. Since only a link can
The proposed scheme can be implemented on top of convey data traffic at a time within a cluster, the sum of the
various physical (PHY) and medium access control airtime ratios of the links in a cluster cannot exceed

.
(MAC) layer protocols that utilize a limited bandwidth Therefore, we have the following constraint:
and divide the time for multiple access, for example, such X
as the carrier sense multiple access/collision avoidance al

; for all c 2 C: ð2Þ
(CSMA/CA), the time division multiple access (TDMA), l2Mc

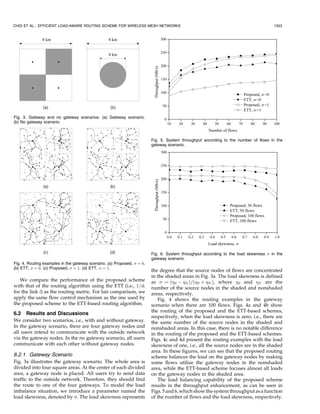
and the reservation ALOHA (R-ALOHA). In Fig. 1, we give an example organization of clusters.
The effective transmission rate of a link is defined as the Note that we do not draw all clusters to avoid over-
number of actually transmitted bits divided by the time crowding. In this figure, four clusters are presented, each of
spent for data transmission, calculated in consideration of which is indicated by a dashed circle. Suppose that a cluster
retransmissions due to errors. That is, the effective transmis- includes all incoming and outgoing links of the nodes in the
sion rate can be calculated as the PHY layer transmission dashed circle. In this example, the clusters 1 and 2 cover the
rate times the probability of successful transmission. The areas around the gateway nodes 1 and 2, respectively.
PHY layer transmission rate can be fixed, or can be When the estimated traffic load around the gateway node 1
adaptively adjusted according to the channel quality by is too high, the user taking the route to the gateway node 1
means of rate control schemes such as the receiver-based may not achieve high data rate due to the constraint (2) for
autorate (RBAR) [23]. In the WMN under consideration, the cluster 1. In this case, if the gateway node 2 is lightly loaded,
effective transmission rate of a link is assumed to be static for it is desirable for the user to choose the route to the gateway
node 2 for higher data rate. Thus, it can be said that the
a long time due to fixed locations of nodes. We define dl as
traffic load is estimated and controlled in the unit of the
the effective transmission rate of the link l.
cluster for global load balancing.
If all flows convey data traffic through each route at their
The notion of a cluster corresponds to a clique in the
flow data rates, the sum of the data P
P rates of traffic passing
“conflict graph” introduced in [24]. In the conflict graph,
through link l is calculated as r2Hl f2Qr f;r , where Hl is
vertices correspond to the links in the WMN. An edge is
defined as the set of the indices of all routes passing through
drawn between two vertices if the corresponding links
the link l, i.e., Hl :¼ fr : l 2 Dr g, and Qr is the indices of all interfere with each other. Thus, an edge stands for confliction
flows that use the route r, i.e., Qr :¼ ff : r 2 Gf g. We define between two vertices. A clique in the conflict graph is a set of
the “airtime ratio” of the link l, denoted by al , as the ratio of vertices that mutually conflict with each other. According to
the time taken up by the transmission to the total time of link [24], unless the conflict graph is a “perfect graph,” the clique
l. The airtime ratio of the link l can be calculated as the sum of constraints in (2) are not tight in the strict sense even when all
the data rates on the link l divided by the effective cliques (clusters) are taken into account. In [25], the authors
transmission rate of the link l. That is, propose the centralized algorithm that transforms the conflict
X X f;r graph to a perfect graph by adding unnecessary edges to the
al ¼ : ð1Þ conflict graph. This algorithm can also be applied to our
r2Hl f2Q
dl
r
routing scheme. However, from a practical point of view, this
Now, we discuss the restriction on the radio resource algorithm is inefficient since it requires centralized control
allocation. For the protocols under consideration, time is the and can overly reduce spatial reuse. Therefore, in this paper,
only radio resource, which is shared by links for data we recommend to use the clique constraints in (2) as it is.

À1
Actually, these clique constraints are enough to serve our duf ðxÞ
¼ xþ1 : ð5Þ
purpose, i.e., identifying overloaded regions in the WMN to dx pf
redirect the routes. Also, there can be too many cliques in the
The marginal utility of a flow is the amount of the utility that
conflict graph, and therefore, considering all of them can
the system can obtain by assigning a unit data rate to the
render the proposed scheme highly complex. From a practical
flow. Thus, to maximize the system utility, the proposed
point of view, the clusters do not need to cover all possible scheme is likely to allocate more data rate to the flow with
cliques, but it is enough for the clusters to be formed in such a large marginal utility. If is large, the marginal utility drops
way that the traffic load in each region of the WMN is quickly as the data rate increases. In this case, the data rates
separately evaluated. tend to be fairly allocated to flows, since the incentive to
3.3 Utility and Delay Penalty as Optimization Target assign more data rate to the flow which has already received
a high data rate reduces. The flow with large value of pf has
The flow with longer distance consumes generally more
a large marginal utility, and therefore, it can receive more
airtime to convey the same amount of data. Therefore, if
data rate.
maximizing system throughput is the optimization target in
the WMN, the flows with short distance are likely to be When the flowP sends data at its flow data rate, the data
f P
allowed to send much more data than those with long rate of flow f is r2Gf f;r . Note that r2Gf f;r is equal to
distance are, which leads to unfair resource allocation among the data rate allocated to one active route, if f is a single-
flows. Thus, we need an optimization target other than the path flow data rate vector. Hence, the utility of flow f is
P
system throughput to take into account the fairness among uf ð r2Gf f;r Þ. If we consider only the utility in the objective
flows. We consider the utility of a flow that represents the function of the optimization problem, the routing algorithm
degree of satisfaction felt by the user using the flow. The is likely to ignore the end-to-end delay on a route. Since the
utility is a highly desirable performance measure since the delay is also of great importance in the practical WMN, we
user satisfaction is the ultimate goal of the network design. incorporate the delay term into the objective function. To do
The utility function defines the mapping between the this, we define the “delay penalty function” for each flow,
data rate of a flow and the utility of that flow. Since the which penalizes the objective function for selecting the
utility function quantifies the network performance per- route with long end-to-end delay. Since the time to transmit
ceived by users when a data rate is given, it can only be a packet of x bits through the link l is given as x=dl , we can
estimated by a subjective survey, not by theoretical
sayP the end-to-end delay on the route r is proportional
that
development. In [26] and [27], the utility function for best
to l2Dr 1=dl . The delay penalty function should have a
effort traffic is derived by analyzing the results from a
subjective survey for various network data applications. larger value when a flow sends more data on the route with
The utility function of a single best effort user is given as long end-to-end delay. Therefore, the delay P
P penalty func-
tion for the flow f can be given as r2Gf f;r l2Dr 1=dl .
uðxÞ ¼ 0:16 þ 0:8 lnðx À 3Þ; ð3Þ Since we have two different objectives (i.e., the utility and
the delay penalty), we should find a Pareto optimal solution
where x is the data rate in the unit of Kilobits per second.
such that no other solution can improve any objective
This utility function is a strictly concave function, and as a
without worsening the other objective. To calculate a Pareto
result, it well shows the law of diminishing marginal utility.
Although the utility function (3) might be best fitted to optimal solution, we use the scalarization technique [28,
the survey results, it is not adequate for theoretical pp. 178-180] that merges multiple objectives into a single
derivation since it is not defined for x 3. Thus, we do objective by taking the weighted sum of the objectives. We
not take the specific values in (3) but adopt only the log introduce the merged objective function as follows:
form of (3) to reflect the law of diminishing marginal utility. 0 1
In this paper, the utility function is designed so as to contain X X XX X 1
the parameters related to system-wide fairness and priority OðÞ :¼
uf @ f;r A À Á f;r ; ð6Þ
f2F r2G f2F r2G l2D
dl
of flows. We define the utility function of flow f as follows: f f r

where :¼ ðf;r Þf2F ;r2Gf and is the “delay penalty para-

pf
uf ðxÞ :¼ ln xþ1 ; ð4Þ meter” that controls the relative importance of the delay
pf
penalty to the utility. We can reduce the end-to-end delay at
where x is the data rate, is the system-wide fairness the expense of the utility by increasing the delay penalty
parameter, and pf represents the priority of flow f. The
parameter. We will demonstrate the impact of the delay
utility function enables us to control the trade-off between
efficiency and fairness by adjusting . With a high value of penalty parameter in Section 6.
, the system-wide fairness can be guaranteed at the cost of
the system throughput. In other words, by increasing the 4 PROPOSED LOAD-AWARE ROUTING SCHEME
value of , the standard deviation of the flow data rates can
be decreased, but the average flow data rate also decreases. In this section, we design the proposed routing scheme by
The parameter pf controls the priority of flow f. The flow using the dual decomposition method. We first formulate the
with high priority pf is likely to enjoy a high data rate. optimization problem from the objective function and the
To explain the reason behind the effect of the parameters, constraints introduced in the previous section, and derive
we introduce the marginal utility. The marginal utility can the dual problem. Next, we explain how to calculate the flow
be derived by differentiating the utility function by the data data rate vector for the given Lagrange multipliers and
rate. That is, suggest the subgradient method to iteratively calculate the

X
optimal Lagrange multipliers. Finally, we propose the s:t: l À c ¼ 0; for l 2 L; ð13Þ
c2V l
dampening algorithm to alleviate the route flapping problem.
c ! 0; for c 2 C: ð14Þ
4.1 Problem Formulation
Ã Ã Ã
We formulate the optimization problem from (1), (2), and Let w :¼ ð ; Þ be any optimal solution of this dual

problem.
(6) as follows:
! 4.2 Flow Data Rate Calculation for Given Lagrange
X X XX X1
max uf f;r À Á f;r ; ð7Þ Multipliers
f2F r2Gf f2F r2Gf
d
l2Dr l Now, we calculate the flow data rates that maximize the
X X f;r Lagrangian (10) for given Lagrange multipliers. To do this,
s:t: al ¼ ; for all l 2 L; ð8Þ
r2Hl f2Qr
dl we find the maximizer of ð f ; Þ over f 2 P f for each flow

X f. Let P f ðÞ denote the set of such maximizers, i.e.,

al

; for all c 2 C; ð9Þ P f ð Þ :¼ arg maxf 2P f ð f ; Þ. The following proposition

l2Mc
holds for the set P f ðÞ:

P
where f;r ! 0 and r2Gf f;r max for all f and r. This Proposition 1. The set P f ð Þ contains at least one single-path

optimization problem is feasible and convex. Let Ã be any
f;r flow data rate vector.
optimal solution of this optimization problem. We also
Proof. The proof is provided in Appendix A. u
t
define the optimal flow data rate vector Ã :¼ ðÃ Þr2Gf .
f f;r
We solve the optimization problem by converting it to
From now on, we will explain how to find a single-path
the dual problem according to the Lagrangian method in
flow data rate vector in P f ðÞ. Let f ð
; Þ be the maximum

[29]. The Lagrangian is given as follows:
value of ðf ; Þ when f is a single-path flow data rate

Âð; a; wÞ
vector with the active route of
. That is,
!
X X XX
X1 X þ l '
:¼ uf f;r ÀÁ f;r f ð
; Þ :¼ max uf ðÞ À : ð15Þ
d 0 max dl
f2F r2Gf f2F r2Gf l2Dr l l2D

X X X f;r ' X X '
þ l al À þ c

À al We define Rf ðÞ :¼ arg max
2Gf f ð
; Þ as the set of the

l2L r2Hl f2Qr
dl c2C l2Mc ð10Þ “optimal routes.” To maximize ðf ; Þ, the active route

!
X X X X þ l ' should be one of the optimal routes in Rf ðÞ. Since uf ðÞ is

¼ uf f;r À f;r a concave function, f ð
; Þ is larger for the active route
P
f2F r2Gf r2Gf l2Dr
dl with the smaller l2D
l =dl . Therefore, we can also write
X X ' X Rf ð Þ as follows:

þ l À c a l þ

c ;
l2L c2V l c2C
X þ l
Rf ð Þ ¼ arg min
: ð16Þ

2Gf dl
where a :¼ ðal Þl2L and V l denotes the set of the indices of all l2D

clusters that the link l belongs to (i.e., V l :¼ fc : l 2 Mc g). It
is noted that we have P We define ð þ l Þ=dl as the “link cost” of the link l. Since
l2D
ð þ l Þ=dl is the sum of link costs on the route
, the
X XX XX X optimal route is the route that minimizes the sum of link
l f;r =dl ¼ f;r l =dl ;
l2L r2Hl f2Qr f2F r2Gf l2Dr
costs. Since most existing ad hoc routing algorithms can
P P P P employ the sum of link costs as the routing metric, the
and c2C c l2Mc al ¼ l2L al c2V l c . In (10), l and c optimal route can be found by applying those ad hoc
are the Lagrange multipliers corresponding to the con- routing algorithms.
straints (8) and (9), respectively. We also define :¼ ðl Þl2L , When f is a single-path flow data rate vector with the
:¼ ðc Þc2C , and w :¼ ð ; Þ.
active route of
, we can maximize ðf ; Þ if the flow data

From the Lagrangian, we define the dual function as rate on the active route is equal to
gðwÞ :¼ max;a Âð; a; wÞ. The dual function gðwÞ is defined

P f ð
; Þ
only for the Lagrange multipliers such that l À c2V l c ¼ X þ l '
0 for l 2 L, since we have gðwÞ ¼ 1 for the other Lagrange :¼ arg max uf ðÞ À
multipliers. Then, the dual function is given as follows: 0 max
l2D
dl ð17Þ
X X !þ '
pf 1
gðwÞ ¼ max ð f ; Þ þ

c ; ð11Þ ¼ min P À1 ; max ;
l2D
ð þ l Þ=dl
f 2P f
f2F c2C
P
where P f :¼ ff : f;r ! 0 for r 2 Gf ; r2Gf f;r max g and
w h e r e ½xŠþ ¼ maxf0; xg. L e t u s d e f i n e f ð
; Þ :¼
P P P
ðf ; Þ :¼ uf ð r2Gf f;r Þ À r2Gf f;r l2Dr ð þ l Þ=dl .
ðf;r ð
; ÞÞr2Gf as follows:
From the dual function, we define the following dual
f ð
; Þ; if r ¼
;
problem: f;r ð
; Þ ¼ ð18Þ
0; otherwise:
min gðwÞ; ð12Þ
Then, we have f ð
; Þ 2 P f ðÞ if
2 Rf ð Þ.


ðjÞ
4.3 Lagrange Multiplier Update jP f ðÃ Þj 1, it is not guaranteed that f ð
f ; ðjÞ Þ converges

From now on, we will find the solution of the dual problem to the optimal flow data rate vector. The cardinality of
(12). The constraint (13) in the dual problem can be P f ð Ã Þ is closely related to the cardinality of Rf ð Ã Þ in (16).

incorporated into the dual function. We define the modified If jRf ð Ã Þj ¼ 1, we also have jP f ð Ã Þj ¼ 1. On the other

dual function hð Þ :¼ gðð ðÞ; ÞÞ, where ð Þ :¼ ðl ðÞÞl2L
hand, if jRf ðÃ Þj 1, the set P f ðÃ Þ contains multiple flow

satisfies the constraint (13) for given . That is, data rate vectors, which include the multipath flow data
X rate vector distributing the data rates on the multiple routes
l ð Þ ¼
c ; ð19Þ in Rf ð Ã Þ. This means that Ã may be the multipath flow
f
c2V l data rate vector for the flow f such that jRf ðÃ Þj 1. In this

ðjÞ
for all l. Then, the dual optimal solution Ã minimizes hðÞ
case, the single-path flow data rate vector f ð
f ; ðjÞ Þ
over c ! 0 for all c 2 C. cannot converge to Ã . However, we can still use
f
ðjÞ
We will use the subgradient method [29, p. 620] to f ð
f ; ðjÞ Þ for all fs as a suboptimal solution very close
calculate the dual optimal solution. We can calculate the to the optimal one, since there are generally a small number
subgradients of h from the theorem of dual derivatives [29, of the flows fs such that jRf ð Ã Þj 1, and the flow data

p. 604]. Recall that
f denotes the active route of the flow f, rates in P f ð Ã Þ well approximate Ã even for fs such that
f
and
¼ ð
f Þf2F denotes the active route vector. We first
jRf ð Ã Þj 1.

ðjÞ
calculate al ð ; Þ, which denotes the airtime ratio of link l

Even when we use f ð
f ; ðjÞ Þ as a suboptimal solution,
when
and are given. The airtime ratio al ð ; Þ is

we still have the “route flapping problem.” The fact that
ðjÞ
calculated as follows: f ð
f ; ðjÞ Þ converges to the set P f ðÃ Þ does not mean

ðjÞ
that f ð
f ; ðjÞ Þ has a limit in P f ð Ã Þ. Therefore, for fs such

X X f;r ð
f ; Þ ðjÞ
al ð ; Þ :¼

: ð20Þ that jP f ð Ã Þj 1, it is possible that f ð
f ; ðjÞ Þ alternates

r2Hl f2Qr
dl between some points in P f ðÃ Þ even after ðjÞ is sufficiently

converged to Ã . In this case, the active route can flap between
From al ð ; Þ, we can calculate sð ; Þ :¼ ðsc ð ; ÞÞc2C ,

some routes in Rf ð Ã Þ. We now suggest the “dampening

which is defined as
algorithm” to solve this route flapping problem.
X
sc ð ; Þ :¼

À

al ð ; ðÞÞ:

ð21Þ
4.5 Dampening Algorithm: Solution to Route
l2Mc
Flapping Problem
If
f 2 Rf ððÞÞ for all f 2 F , the vector sð ; Þ is the

The dampening algorithm should alleviate the route flapping
subgradient of hðÞ. problem while keeping the solution in the close range of the
Let ðjÞ :¼ ððjÞ Þc2C be the estimation of Ã at the jth
c optimal one. Moreover, the dampening algorithm should be
iteration of the subgradient method. We also define
ðjÞ :¼ able to be implemented in a distributed way. To accomplish
ðjÞ ðjÞ
ð
f Þf2F as the active route vector such that
f 2 Rf ðððjÞ ÞÞ
these goals, the dampening algorithm prevents the route
for all f 2 F . The iteration begins when j ¼ 1. The initial flapping by changing the active route more conservatively
values should satisfy ð0Þ ! 0 for all c 2 C. The Lagrange
c than the original algorithm does. When the original algo-
ðjÞ
multipliers are updated at the jth iteration as follows: rithm is used, we have
f 2 Rf ð ðjÞ Þ. This means that, at the

Â À ÁÃþ jth iteration, the original algorithm finds any optimal route in
ðjþ1Þ ¼ ðjÞ À ðjÞ s
ðjÞ ; ðjÞ
; ð22Þ Rf ð ðjÞ Þ from (16), and immediately changes the active route

to the new optimal route. However, the dampening algo-
where ½ðxc Þc2C Šþ ¼ ðmaxf0; xc gÞc2C and ðjÞ is the step size.
rithm changes the active route only if the new route increases
The step size can be the diminishing step size that satisfies
P1 ðjÞ P1 ðjÞ 2 f ð
; ðjÞ Þ by a certain margin.
ðjÞ 0, j¼0 ¼ 1, and j¼0 ð Þ 1. In this case, Let us explain the operation of the dampening algorithm.
ðjÞ converges to Ã . Alternatively, we can also use the We define as the “dampening parameter” which controls
constant step size, which makes ðjÞ converge to within the conservativeness in changing the route. The value of is
ðjÞ
some range of Ã . We define ðjÞ :¼ ðl Þl2L ¼ ððjÞ Þ. Then,
between zero and one. If is set to one, the dampening
ðjÞ converges to Ã when ðjÞ converges to Ã . algorithm is the same as the original algorithm. The active
route is changed more conservatively with the smaller value
4.4 Convergence of Flow Data Rate
ðjÞ of . At the jth iteration, the dampening algorithm first finds
We take f ð
f ; ðjÞ Þ as the estimation of the optimal flow ðjÞ
any optimal route in Rf ð ðjÞ Þ. Let yf denote the optimal route

data rate vector Ã at jth iteration. We will discuss the
f for the flow f, newly found at the jth iteration. The
convergence of this flow data rate vector. Since the ðjÞ
dampening algorithm decides the active route
f according
optimization problem (7) is strictly feasible and the objective
to the following rules:
and constraint functions are concave, the strong duality
ðjÀ1Þ ðjÞ
holds from the Slater’s constraint qualification [29, p. 520]. . If f ð
f ; ðjÞ Þ ! Á f ðyf ; ðjÞ Þ, the dampening
Therefore, Ã is included in the set P f ð Ã Þ. Moreover,
f algorithm does not change the active route, i.e.,
ðjÞ
f ð
f ; ðjÞ Þ also converges to the set P f ð Ã Þ as j ! 1, since
ðjÞ ðjÀ1Þ
ðjÞ
f ¼
f .
we have f ð
f ; ðjÞ Þ 2 P f ð ðjÞ Þ for all j.
ðjÀ1Þ ðjÞ
From the above statements, we can conclude that . If f ð
f ; ðjÞ Þ Á f ðyf ; ðjÞ Þ, the dampening
ðjÞ algorithm changes the active route to the new
f ð
f ; ðjÞ Þ converges to Ã as j ! 1 for the flow f such
f ðjÞ ðjÞ
that jP f ð Ã Þj ¼ 1. However, for the flow f such that
optimal route, i.e.,
f ¼ yf .

Efficient load aware routing scheme

More Related Content

What's hot

Viewers also liked

Similar to Efficient load aware routing scheme

More from ambitlick

Recently uploaded

Efficient load aware routing scheme