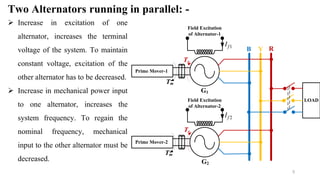
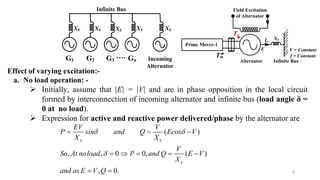
This document discusses an alternator connected to an infinite bus. It defines an infinite bus as a constant voltage and frequency source that can absorb or supply reactive power without changing its characteristics. The document explains that at no load, an alternator synchronized to an infinite bus is in a floating condition where it delivers or absorbs no real or reactive power. It then describes what happens when the alternator's excitation is increased or decreased. An increase leads to reactive power delivery, while a decrease leads to reactive power absorption from the infinite bus, as the alternator's emf changes relative to the bus voltage. In both cases, an armature current is established to maintain the alternator's constant air-gap flux.

1. Electrical Machines-II
6th Semester, EE and EEE
By
Dr. Binod Kumar Sahu
Associate Professor, Electrical Engg.
Siksha ‘O’ Anusandhan, Deemed to be University,
Bhubaneswar, Odisha, India
Lecture-20

2. 2
Learning Outcomes: - (Previous Lecture_19)
 Numerical on Effect of varying field excitation on two alternators running in
parallel:

3. 3
Learning Outcomes: - (Today’s Lecture_20)
 Synchronous generator (Alternator) on an infinite bus.
 Effect of change in varying excitation on an alternator connected to infinite
bus at no load.

4. 4
Alternator on an Infinite Bus: -
Infinite Bus: -
 A bus-bar that maintains constant voltage and constant frequency irrespective of the
load variation on it is called an infinite bus.
 A large number of alternators interconnected together to form a supply system
may be regarded as an infinite bus.
 So, an infinite bus is a voltage source having zero internal impedance and infinite
rotational inertia.
 Therefore, a synchronous machine switched on to or disconnected from the infinite
bus, can not change the voltage and frequency of the supply system.

5. 5
YB R
LOAD
G2
Prime Mover-2
G1
Prime Mover-1
Te
Tm
Tm
Te
1fI
2fI
Field Excitation
of Alternator-1
Field Excitation
of Alternator-2
Two Alternators running in parallel: -
 Increase in excitation of one
alternator, increases the terminal
voltage of the system. To maintain
constant voltage, excitation of the
other alternator has to be decreased.
 Increase in mechanical power input
to one alternator, increases the
system frequency. To regain the
nominal frequency, mechanical
input to the other alternator must be
decreased.

6. 6
Effect of varying excitation:-
a. No load operation: -
 Initially, assume that |E| = |V| and are in phase opposition in the local circuit
formed by interconnection of incoming alternator and infinite bus (load angle δ =
0 at no load).
 Expression for active and reactive power delivered/phase by the alternator are
G1 G2 G3 Gn
…. Incoming
Alternator
Infinite Bus
XSXS XS XSXS
Infinite BusAlternator
XS
V = Constant
f = Constant
Ia
E
Field Excitation
of Alternator
Prime Mover-1
Te
Tm
( )
, , 0 0, ( )
, 0.
s s
s
EV V
P sin and Q Ecos V
X X
V
So At noload P and Q E V
X
and as E V Q
 

  
    
 

7. 7
 Voltage equation of the alternator is:
 As δ = 0, and E = V => Ia = 0. So, the active and
reactive power delivered by the alternator:
 So at no load, no power is delivered to or, received
from the infinite bus. Therefore the alternator is said to
be in floating condition.
 Now, if the excitation of alternator is increased,
induced emf of alternator ‘E’ becomes more than bus-
bar voltage ‘V’.
 So, active and reactive power becomes:
0 0a aP VI cos and Q VI sin    
a sE V j I X
  
 
( )
, , 0 0,
, ( )
s s
s
EV V
P sin and Q E V
X X
So At noload P
V
Wehaveincreased theexcitation so E V Q E V ve
X


  
  
     
V
E E V
f
r a sE I X
aI
E
V
E
V
r a sE I X
'f f

8. 8
 As ‘Q’ is positive, the alternator delivers lagging reactive power to the infinite bus.
 The resultant emf ‘Er = E – V = IaXs’ gives rise to armature current ‘Ia’, which lags ‘E’ by
900 and leads bus voltage ‘V’ by 900.
 This armature current produces demagnetizing effect to maintain constant air-gap flux (as
the alternator is connected to a constant voltage and constant frequency source its air-gap
flux is always constant).
 Under this condition,
0 0
(90 ) 0 (90 )a a aP VI cos and Q VI sin VI   

9. 9
 Now, if the excitation of alternator is decreased,
induced emf of alternator ‘E’ becomes less than bus-
bar voltage ‘V’.
 So the active and reactive power becomes:
 Decrease in excitation of alternator, reduces its
induced emf causing armature current ‘Ia’.
( )
, , 0 0,
, ( )
s s
s
EV V
P sin and Q E V
X X
So At noload P
V
Wehavedecreased theexcitation E V Q E V ve
X


  
  
     
aI
E
V
r a sE I X
'f
V
E
f

10. 10
 As ‘Q’ is negative, the alternator receives lagging reactive power or delivers
leading reactive power to the infinite bus.
 Now, in this case armature current ‘Ia’ leads induced emf (E) by 900 which
increases the air-gap flux, due to magnetizing effect of armature reaction. This
magnetizing effect again maintains a constant air-gap flux.
 Under this condition,
 So any change in field excitation, automatically sets in an armature current
‘Ia’ which helps in regaining the synchronism.
0 0
( 90 ) 0 ( 90 )a a aP VI cos and Q VI sin VI      

11. 11
Thank you