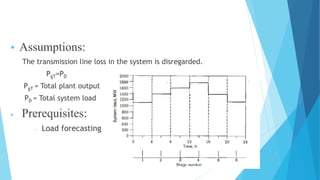
This document discusses unit commitment in power systems. Unit commitment aims to schedule generating units to meet forecasted load at minimum cost while maintaining reliability. It considers startup costs, operating costs, and shutdown costs over a daily load cycle. Dynamic programming is used to solve the unit commitment problem by evaluating combinations of generating units at each time interval and carrying minimum costs backward from the final interval to find the overall lowest-cost solution. The objective is to determine the optimal set of units to operate at each time period to supply predicted load economically.

1. ECONOMIC OPERATION OF POWER
SYSTEMS BY UNIT COMMITMENT
Department Of Electrical And Electronics Engineering
IIIT Bhubaneswar
Bhubaneswar- 756003, Odisha

2. ECONOMIC OPERATION OF POWER
SYSTEMS BY UNIT COMMITMENT
Seminar presented by
PRITESH PRIYADARSHI
(B311029)
under the guidance of
Dr. P K RAY
Department Of Electrical And Electronics Engineering
IIIT Bhubaneswar

3. OUTLINE:
1. Why Unit Commitment ?
2. What is Unit commitment ?
3. Difference between Economic Load Dispatch & Unit Commitment
4. Unit Commitment Terminology
5. Unit Commitment Procedure
6. Solving The Unit Commitment Problem (Dynamic Programming)

4. Why Unit Commitment

5. What is Unit Commitment:
 Unit commitment plans for best set of units to be available to supply the predicted or
forecast load of the system over a future time period.
 “Unit Commitment” is therefore, one way to suggest, just sufficient number of
generating units with sufficient amount of generating capacity to meet a given load
economically with sufficient reserve capacity to meet any abnormal, operating
condition.
 Here we consider the problem of scheduling fossil fired thermal units in which the
aggregate costs( such as start up cost, operating fuel costs & shut down costs ) are to
be minimized over a daily load cycle.

6. Difference between Economic Load
Dispatch & Unit Commitment :
1. Economic Load Dispatch
a) It’s a short term determination.
b) Dispatch at lowest possible cost
1. Unit Commitment
a) Unit commitment aims to make power system
reliable

7.  Assumptions:
The transmission line loss in the system is disregarded.
PgT=PD
PgT = Total plant output
PD = Total system load
 Prerequisites:
 Load forecasting

8.  If we have “K” generating units(no two identical), then
there are
(2k – 1) number of combinations.
 For example if K=4, then there are 15 theoretically
possible combinations.

9.  Xi(k) = combination Xi of interval k
 Pi(k) = minimum production cost of combination Xi(k)
 Tij(k) = cost of transition from combination Xi(k) to combination Xj(k+1)
between intervals k and k+1
 Fij(k) = The cost associated with any stage k
Fij(k) = Pi(k) + Tij(k)

10. Unit Commitment Procedure:

11. Dynamic Programming:
 We use “Dynamic programming” to solve Unit Commitment problem.
 Here we take an iterative relation embodying the principle that starting with
given combination Xi* at stage k, the minimum unit commitment cost is found
by minimizing the sum of the current single-stage cost fij(k) plus the minimum
cumulative cost Fij(k+1) over the later stages of study.
 This is one example of the principle of optimality, which states: if possible
path from A to C passes through intermediate point B , then the best possible
path from B to C must be corresponding part of the best path from A to C.
 Computationally, we evaluate one decision at a time beginning with the final
stage N and carry the minimum cumulative cost function backward in time to
stage k to find the minimum cumulative cost Fi*(k) for the feasible
combination.

12. Contd.
 The minimum cumulative cost decisions are recovered as we sweep from stage 1
to stage N searching through the tables already calculated for each stage. This
computational procedure is known as Dynamic Programming.2
 It involves two sweeps through each stage k.
 In the first sweep, which is computationally intensive, we work backward
computing and recording for each candidate combination xi of stage k the
minimum Fi(k) and its associated xj(k+1).
 The second sweep in the forward direction does not involve any processing since
with xi*(k) identified we merely enter the table of results already recorded to
retrieve the value Fi*(k) and its associated combination xj(k+1), which becomes
xi*(k+1) as we move to next forward stage.

14. References:
 “Power system Analysis” by John J. Grainger, William D. Stevenson
 R. Bellman, Dynamic Programming, Princeton University Press, Princeton, NJ,
1957.