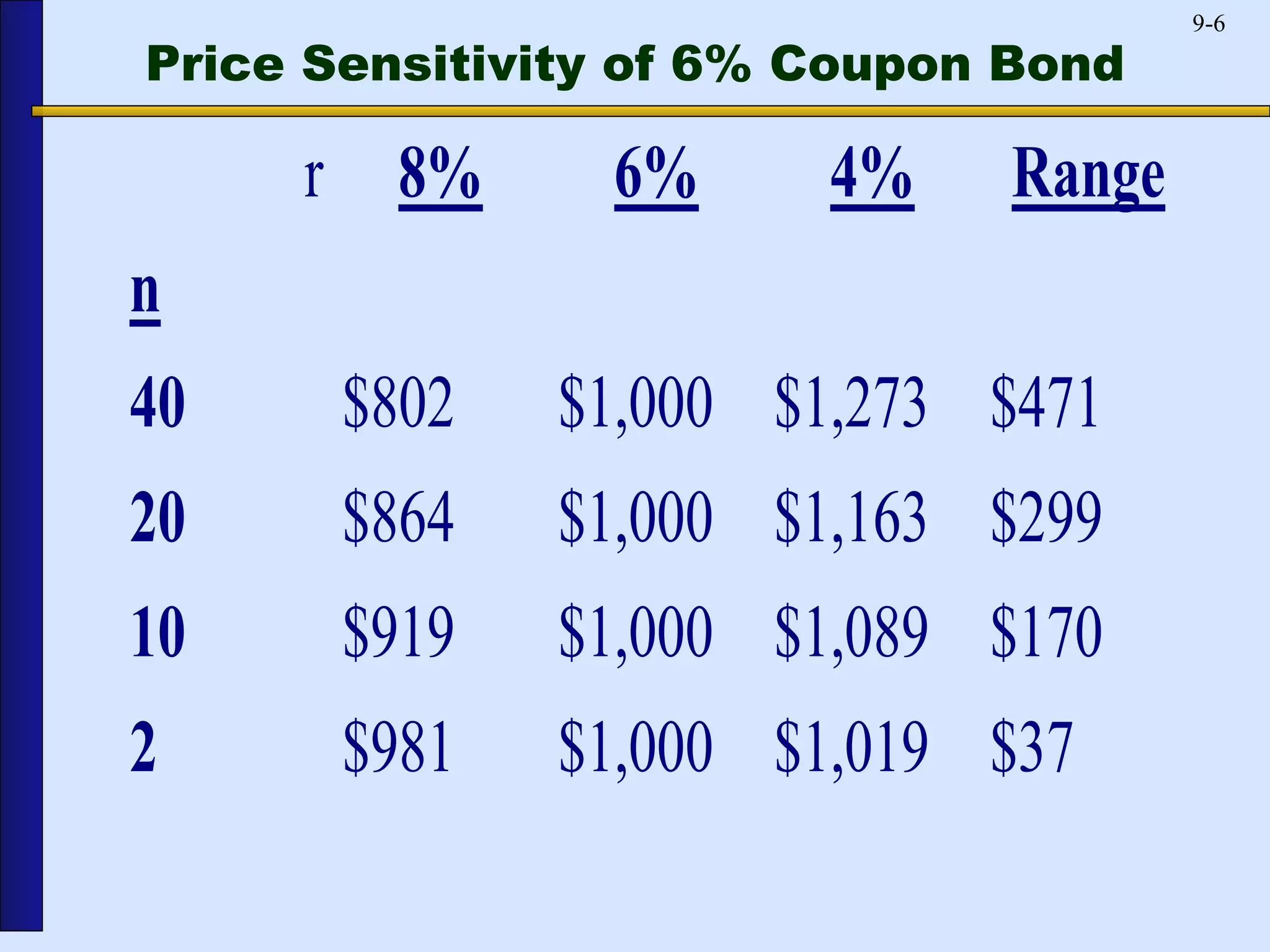
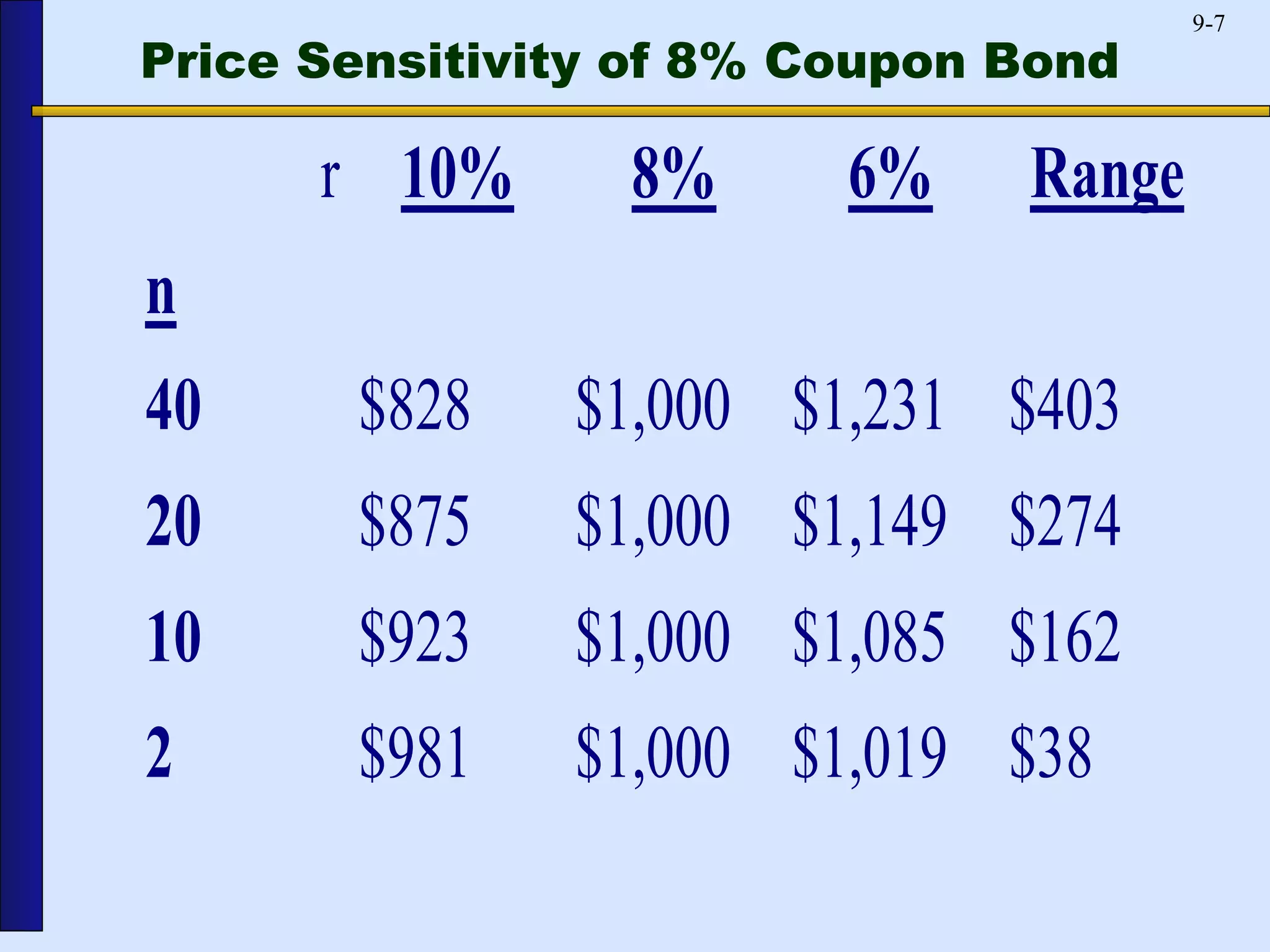
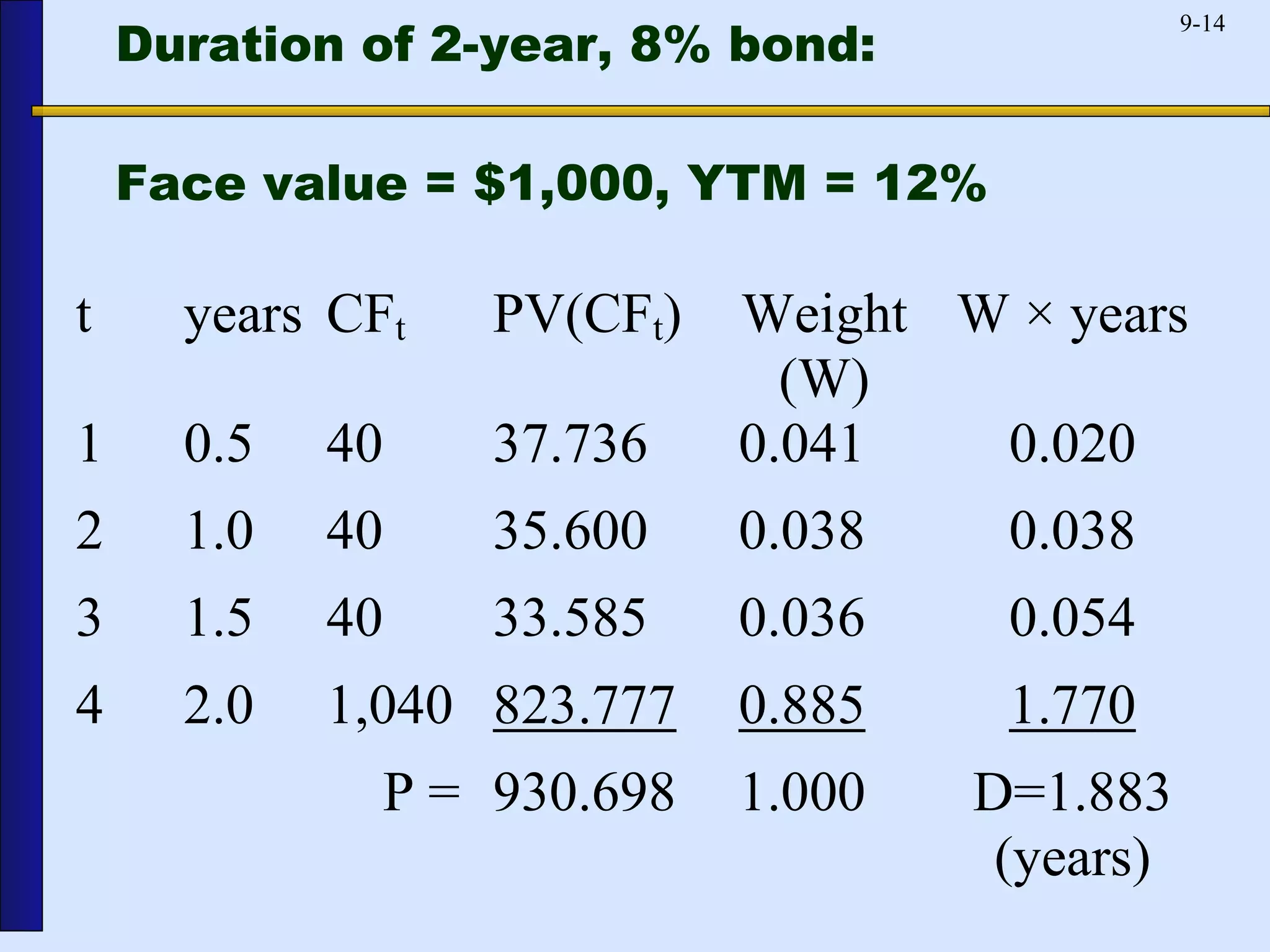
This document discusses duration, a model for measuring interest rate risk. Duration is a measure of how the price of a bond or loan will change in response to changes in interest rates. It represents the weighted average time until cash flows are received. Longer maturity bonds and loans have higher durations, meaning their prices are more sensitive to interest rate changes. Bonds with higher coupons have lower durations. Duration can be used to immunize a financial institution's balance sheet against interest rate risk by matching asset and liability durations.

1. Interest Rate Risk -Duration model

2. Overview This chapter discusses a market value-based model for assessing and managing interest rate risk: Duration Computation of duration Economic interpretation Immunization using duration * Problems in applying duration

3. Price Sensitivity and Maturity In general, the longer the term to maturity, the greater the sensitivity to interest rate changes. Example: Suppose the zero coupon yield curve is flat at 12%. Bond A pays $1762.34 in five years. Bond B pays $3105.85 in ten years, and both are currently priced at $1000.

4. Example continued... Bond A: P = $1000 = $1762.34/(1.12) 5 Bond B: P = $1000 = $3105.84/(1.12) 10 Now suppose the interest rate increases by 1%. Bond A: P = $1762.34/(1.13) 5 = $956.53 Bond B: P = $3105.84/(1.13) 10 = $914.94 The longer maturity bond has the greater drop in price because the payment is discounted a greater number of times .

5. Coupon Effect Bonds with identical maturities will respond differently to interest rate changes when the coupons differ. This is more readily understood by recognizing that coupon bonds consist of a bundle of “zero-coupon” bonds. With higher coupons, more of the bond’s value is generated by cash flows which take place sooner in time. Consequently, less sensitive to changes in R.

6. Price Sensitivity of 6% Coupon Bond

7. Price Sensitivity of 8% Coupon Bond

8. Remarks on Preceding Slides In general, longer maturity bonds experience greater price changes in response to any change in the discount rate. The range of prices is greater when the coupon is lower. The 6% bond shows greater changes in price in response to a 2% change than the 8% bond. The first bond has greater interest rate risk.

9. Duration Duration Weighted average time to maturity using the relative present values of the cash flows as weights. Combines the effects of differences in coupon rates and differences in maturity. Based on elasticity of bond price with respect to interest rate.

10. Duration Duration D =  N t=1 [CF t • t/(1+R) t ]/  N t=1 [CF t /(1+R) t ] Where D = duration t = number of periods in the future CF t = cash flow to be delivered in t periods N= time-to-maturity R = yield to maturity.

11. Duration Since the price (P) of the bond must equal the present value of all its cash flows, we can state the duration formula another way: D =  N t=1 [t  (Present Value of CF t /P)] Notice that the weights correspond to the relative present values of the cash flows.

12. Duration of Zero-coupon Bond For a zero coupon bond, duration equals maturity since 100% of its present value is generated by the payment of the face value, at maturity. For all other bonds: duration < maturity

13. Computing duration Consider a 2-year, 8% coupon bond, with a face value of $1,000 and yield-to-maturity of 12%. Coupons are paid semi-annually. Therefore, each coupon payment is $40 and the per period YTM is (1/2) × 12% = 6%. Present value of each cash flow equals CF t ÷ (1+ 0.06) t where t is the period number.

14. Duration of 2-year, 8% bond: Face value = $1,000, YTM = 12%

15. Special Case Maturity of a consol: M =  . Duration of a consol: D = 1 + 1/R

16. Duration Gap Suppose the bond in the previous example is the only loan asset (L) of an FI, funded by a 2-year certificate of deposit (D). Maturity gap: M L - M D = 2 -2 = 0 Duration Gap: D L - D D = 1.885 - 2.0 = -0.115 Deposit has greater interest rate sensitivity than the loan, so DGAP is negative. FI exposed to rising interest rates.

17. Features of Duration Duration and maturity: D increases with M, but at a decreasing rate. Duration and yield-to-maturity: D decreases as yield increases. Duration and coupon interest: D decreases as coupon increases

18. Economic Interpretation Duration is a measure of interest rate sensitivity or elasticity of a liability or asset: [ Δ P/P]  [ Δ R/(1+R)] = -D Or equivalently, Δ P/P = -D[ Δ R/(1+R)] = -MD × Δ R where MD is modified duration.

19. Economic Interpretation To estimate the change in price, we can rewrite this as: Δ P = -D[ Δ R/(1+R)]P = -(MD) × ( Δ R) × (P) Note the direct linear relationship between Δ P and -D.

20. Semi-annual Coupon Payments With semi-annual coupon payments: ( Δ P/P)/( Δ R/R) = -D[ Δ R/(1+(R/2)]

21. An example: Consider three loan plans, all of which have maturities of 2 years. The loan amount is $1,000 and the current interest rate is 3%. Loan #1, is a two-payment loan with two equal payments of $522.61 each. Loan #2 is structured as a 3% annual coupon bond. Loan # 3 is a discount loan, which has a single payment of $1,060.90.

22. Duration as Index of Interest Rate Risk

23. Immunizing the Balance Sheet of an FI Duration Gap: From the balance sheet, E=A-L. Therefore,  E=  A-  L. In the same manner used to determine the change in bond prices, we can find the change in value of equity using duration.  E = [-D A A + D L L]  R/(1+R) or  E  D A - D L k]A(  R/(1+R))

24. Duration and Immunizing The formula shows 3 effects: Leverage adjusted D-Gap The size of the FI The size of the interest rate shock

25. An example: Suppose D A = 5 years, D L = 3 years and rates are expected to rise from 10% to 11%. (Rates change by 1%). Also, A = 100, L = 90 and E = 10. Find change in E.  D A - D L k]A[  R/(1+R)] = -[5 - 3(90/100)]100[.01/1.1] = - $2.09. Methods of immunizing balance sheet. Adjust D A , D L or k.

26. Immunization and Regulatory Concerns Regulators set target ratios for an FI’s capital (net worth): Capital (Net worth) ratio = E/A If target is to set  (E/A) = 0: D A = D L But, to set  E = 0: D A = kD L

27. *Limitations of Duration Immunizing the entire balance sheet need not be costly. Duration can be employed in combination with hedge positions to immunize. Immunization is a dynamic process since duration depends on instantaneous R. Large interest rate change effects not accurately captured. Convexity More complex if nonparallel shift in yield curve.

28. *Duration Measure: Other Issues Default risk Floating-rate loans and bonds Duration of demand deposits and passbook savings Mortgage-backed securities and mortgages Duration relationship affected by call or prepayment provisions.