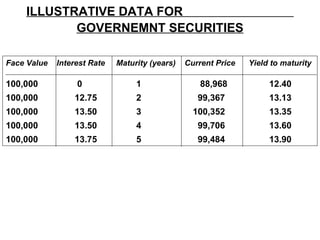
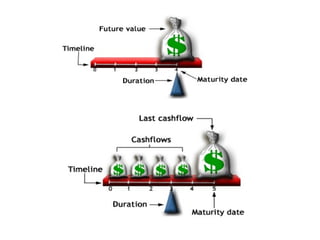
This document discusses different types of bonds and bond characteristics such as par value, coupon rate, maturity date, and callability. It explains how to calculate bond yields such as current yield, yield to maturity, and yield to call. The key valuation models discussed are the present value model, which values a bond based on its expected cash flows discounted at the yield to maturity, and the yield model, which solves for the yield given the bond's market price. The document also covers factors that impact bond prices such as interest rates, maturity, and coupon rate. Bond duration, a measure of price sensitivity to interest rates, is introduced along with related concepts like modified duration.

1. Types of Bonds Coupon bonds and zero coupon bonds Convertible and non-convertible bonds Infrastructure bonds RBI relief bonds Tax savings bonds Government bonds and corporate bonds Municipal bonds

2. Bond Characteristics A bond is described in terms of: Par value Coupon rate Liquidity Maturity date Callability Re-investment Risk

3. The Fundamentals of Bond Valuation The present-value model Where: P m =the current market price of the bond n = the number of years to maturity C i = the annual coupon payment for bond i i = the prevailing yield to maturity for this bond issue P p =the par value of the bond

4. The Present Value Model The value of the bond equals the present value of its expected cash flows where: P m = the current market price of the bond n = the number of years to maturity C i = the annual coupon payment for Bond I i = the prevailing yield to maturity for this bond issue P p = the par value of the bond

5. The Yield Model The expected yield on the bond may be computed from the market price where: i = the discount rate that will discount the cash flows to equal the current market price of the bond

6. Computing Bond Yields Yield Measure Purpose Nominal Yield Measures the coupon rate Current yield Measures current income rate Promised yield to maturity Measures expected rate of return for bond held to maturity Promised yield to call Measures expected rate of return for bond held to first call date Realized (horizon) yield Measures expected rate of return for a bond likely to be sold prior to maturity. It considers specified reinvestment assumptions and an estimated sales price. It can also measure the actual rate of return on a bond during some past period of time.

7. Nominal Yield Measures the coupon rate that a bond investor receives as a percent of the bond’s par value

8. Current Yield Similar to dividend yield for stocks Important to income oriented investors CY = C i /P m where: CY = the current yield on a bond C i = the annual coupon payment of bond i P m = the current market price of the bond

9. Promised Yield to Maturity Widely used bond yield figure Assumes Investor holds bond to maturity All the bond’s cash flow is reinvested at the computed yield to maturity

10. Computing the Promised Yield to Maturity Solve for i that will equate the current price to all cash flows from the bond to maturity, similar to IRR

11. Computing Promised Yield to Call where: P m = market price of the bond C i = annual coupon payment nc = number of years to first call P c = call price of the bond

12. Realized (Horizon) Yield Present-Value Method

13. Calculating Future Bond Prices where: P f = estimated future price of the bond C i = annual coupon payment n = number of years to maturity hp = holding period of the bond in years i = expected semiannual rate at the end of the holding period

14. REALISED YIELD TO MATURITY FUTURE VALUE OF BENEFITS (1+ r* ) 5 = 2032 / 850 = 2.391 r* = 0.19 OR 19 PERCENT

15. Yield Adjustments for Tax-Exempt Bonds Where: FTEY = fully taxable yield equivalent i = the promised yield on the tax exempt bond T = the amount and type of tax exemption (i.e., the investor’s marginal tax rate)

16. Bond Valuation Using Spot Rates where: P m = the market price of the bond C t = the cash flow at time t n = the number of years i t = the spot rate for Treasury securities at maturity t

17. What Determines Interest Rates Inverse relationship with bond prices Forecasting interest rates Fundamental determinants of interest rates i = RFR + I + RP where: RFR = real risk-free rate of interest I = expected rate of inflation RP = risk premium

18. What Determines Interest Rates Effect of economic factors real growth rate tightness or ease of capital market expected inflation or supply and demand of loanable funds Impact of bond characteristics credit quality term to maturity indenture provisions foreign bond risk including exchange rate risk and country risk

19. Spot Rates and Forward Rates Creating the Theoretical Spot Rate Curve Calculating Forward Rates from the Spot Rate Curve

20. ILLUSTRATIVE DATA FOR GOVERNEMNT SECURITIES Face Value Interest Rate Maturity (years) Current Price Yield to maturity 100,000 0 1 88,968 12.40 100,000 12.75 2 99,367 13.13 100,000 13.50 3 100,352 13.35 100,000 13.50 4 99,706 13.60 100,000 13.75 5 99,484 13.90

21. FORWARD RATES 88968 100000 • ONE - YEAR TB RATE 100000 88968 = r 1 = 0.124 (1 + r 1 ) • 2 - YEAR GOVT. SECURITY 12750 112750 99367 = + + r 2 = 0.1289 (1.124) (1.124) (1 + r 2 ) • 3 - YEAR GOVT. SECURITY 13500 13500 113500 100352 = + + (1.124) (1.124) (1 .1289) (1.124) (1.1289) (1 + r 3 ) r 3 = 0.1512

22. Term Structure of Interest Rates It is a static function that relates the term to maturity to the yield to maturity for a sample of bonds at a given point in time. Term Structure Theories Expectations hypothesis Liquidity preference hypothesis Segmented market hypothesis or preferred habitat theory or institutional theory or hedging pressure theory

23. Expectations Hypothesis Any long-term interest rate simply represents the geometric mean of current and future one-year interest rates expected to prevail over the maturity of the issue

24. Liquidity Preference Theory Long-term securities should provide higher returns than short-term obligations because investors are willing to sacrifice some yields to invest in short-maturity obligations to avoid the higher price volatility of long-maturity bonds

25. Segmented-Market Hypothesis Different institutional investors have different maturity needs that lead them to confine their security selections to specific maturity segments

26. Trading Implications of the Term Structure Information on maturities can help you formulate yield expectations by simply observing the shape of the yield curve

27. Yield Spreads Segments: government bonds, agency bonds, and corporate bonds Sectors: prime-grade municipal bonds versus good-grade municipal bonds, AA utilities versus BBB utilities Coupons or seasoning within a segment or sector Maturities within a given market segment or sector

28. Yield Spreads Magnitudes and direction of yield spreads can change over time

29. What Determines the Price Volatility for Bonds Bond price change is measured as the percentage change in the price of the bond Where: EPB = the ending price of the bond BPB = the beginning price of the bond

30. What Determines the Price Volatility for Bonds Four Factors 1. Par value 2. Coupon 3. Years to maturity 4. Prevailing market interest rate

31. What Determines the Price Volatility for Bonds Five observed behaviors 1. Bond prices move inversely to bond yields (interest rates) 2. For a given change in yields, longer maturity bonds post larger price changes, thus bond price volatility is directly related to maturity 3. Price volatility increases at a diminishing rate as term to maturity increases 4. Higher coupon issues show smaller percentage price fluctuation for a given change in yield, thus bond price volatility is inversely related to coupon

32. What Determines the Price Volatility for Bonds The maturity effect The coupon effect The yield level effect Some trading strategies

33. The Duration Measure Since price volatility of a bond varies inversely with its coupon and directly with its term to maturity, it is necessary to determine the best combination of these two variables to achieve your objective A composite measure considering both coupon and maturity would be beneficial Duration is defined as a bond’s price sensitivity to interest rate changes Higher the duration, greater is the sensitivity Number of years to recover the trust cost of a bond

34. The Duration Measure For instance, if the interest rate increases from 6% to 7%, the price of a bond with 5 years duration will move down by 5%, and that of 10 years duration by 10%....... so on. Variables that affect the duration are: Coupon Rate YTM Interest Rate changes

35. The Duration Measure Developed by Frederick R. Macaulay, 1938 Where: t = time period in which the coupon or principal payment occurs C t = interest or principal payment that occurs in period t i = yield to maturity on the bond

37. Characteristics of Macaulay Duration Duration of a bond with coupons is always less than its term to maturity because duration gives weight to these interim payments A zero-coupon bond’s duration equals its maturity There is an inverse relationship between duration and coupon There is a positive relationship between term to maturity and duration, but duration increases at a decreasing rate with maturity There is an inverse relationship between YTM and duration

38. Modified Duration and Bond Price Volatility An adjusted measure of duration can be used to approximate the price volatility of an option-free (straight) bond Where: m = number of payments a year YTM = nominal YTM

39. Modified Duration and Bond Price Volatility Bond price movements will vary proportionally with modified duration for small changes in yields An estimate of the percentage change in bond prices equals the change in yield time modified duration Where:  P = change in price for the bond P = beginning price for the bond D mod = the modified duration of the bond  i = yield change in basis points divided by 100