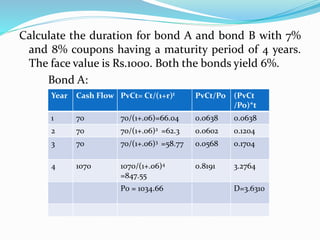
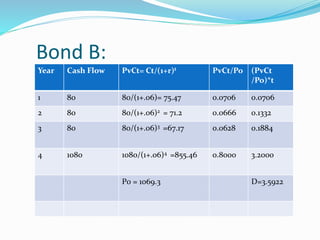
A bond is a contract where the borrower pays interest to the lender. Bonds have risks like interest rate risk, default risk, marketability risk, and callability risk. The time value of money concept states that money received today is worth more than money received in the future. Key metrics for bonds include holding period return, current yield, yield to maturity, and duration. Duration measures a bond's interest rate sensitivity - the higher the duration, the more sensitive the bond is to interest rate changes.

2. Bond
 A bond is a contract that requires the borrower to pay an
interest to the lender.
 It is issued by the government or corporations.
 The par value of the bond indicates the face value of the
bond and the face value may be Rs. 1000, Rs.2000, Rs.5000
and the like.
 Most bonds offer fixed interest payments till the maturity.
 The interest rates are known as the coupon rates and are
paid quarterly, semiannually and annually.

3. Bond Risk
 Interest Rate Risk : If the market interest rate moves up ,
the price of the bond declines and vice-versa.
 Default Risk : The failure to pay the agreed value of the
debt instrument by the issuer in full, on time or both.
 Marketability Risk : Variations in return caused by
difficulties in selling the bonds quickly without making a
substantial price concession.
 Callability Risk: The uncertainty in getting the return due
to the issuers’ ability to call the bond at any time.

4. Time Value Concept
 A rupee received today is more valuable than a rupee
received tomorrow.
Future Value = Present Value (1+ interest rate)t
Present Value = Future Value / (1+ interest rate)t

5. Bond Return
 Holding Period Return: When an investor buys a
bond and sells it after holding it for a while, the rate of
return in that holding period is known as holding
period return.
HPR = (Price gain or loss during the holding period +
Coupon interest rate ) / (Price at the beginning of the
holding period)

6. 1. An investor purchase a bond at Rs. 900 with Rs.100
as coupon payment and sells it at Rs.1000. What is
his holding period return?
2. If the bond is sold for Rs. 750 after receiving Rs.100 as
coupon payment, what is the holding period return?
1. HPR = (100 + 100)/900 = 200/900 = 22.22%
2. HPR = (-150+100)/900 = -50/900 = -5.5%

7. Current Yield
It is the coupon payment as a percentage of current
market price.
Current Yield = Annual Coupon Payment
--------------------------------
Current Market Price
 It helps to know the rate of cash flow from the
investment every year.

8. Yield To Maturity
YTM is the rate of return that an investor can expect to
earn if the bond is held till maturity.
Assumptions:
 There should not be any default – Principal and
coupon amount should be paid as per schedule.
 The investor has to hold the bond till maturity.
 All coupon payments should be reinvested
immediately at the same interest rate as the YTM of
the bond.

9. YTM
YTM = C + (P or D / years to maturity)
------------------------------------
(P0 + F)/2
Where Y = Yield to Maturity, C = Coupon Interest,
P or D = Premium or Discount P0 = Present Value
F = Face Value.
P or D = Redemption value- Market Price
 Based on YTM, present price of the bond can be found.
 If the prevailing price is greater than the calculated price,
then the bond is over priced and vice-versa.

10. A 4 year bond with a 7% coupon rate and maturity value
of Rs. 1000 is currently selling at Rs.905. What is its
YTM?
YTM = C + (P or D / years to maturity)
------------------------------------
(P0 + F)/2
YTM = 70 + (95/4) 70 +23.75 93.75
------------- = ---------- = --------
(905+1000)/2 952.5 952.5
YTM = 9.8 %

11. A Rs.100 par value bond bearing a coupon rate of 11%
matures after 5 years. The expected yield to maturity is
15%. The present market price is Rs.82. Can the investor
buy it ?
NPV = Coupon + Pm
--------- ------
(1+y)t (1+y)t
where NPV = Net Present Value Pm = Market Price
NPV = (11) (PVAF (15, 5))+ (100)(PVF (15, 5))= 11 *3.352 +
100*0.497 = 36.87 + 49.7 = 86.57
NPV = (11)/(1+.15)1 + (11)/(1+.15)2 + (11)/(1+.15)3 +
(11)/(1+.15)4 + (11)/(1+.15)5 + (100)/(1+.15)5 = {9.57 + 8.32
+ 7.23 + 6.29 + 5.47 }+ 49.72 = 36.88 + 49.72 = 86.6
NPV = Rs.86.6, Present Market Price = Rs.82
Since PMP< NPV, Bond is under priced and the investor can
buy the bond.

12. Bond Value Theorems
 Bond value depends on three factors - coupon rate,
years to maturity, expected yield to maturity or
required rate of return.
Theorem 1: If the market price of bond increases, the
yield would decline and vice-versa.
Theorem 2: If the bond’s yield remains the same over its
life , the discount or premium depends on the maturity
period.
Theorem 3: If the bond’s yield remains constant over its
life , the discount or premium amount will decrease at
an increasing rate as its life gets shorter.

13. Theorem 4 : A rise in the bond’s price for a decline in
the bond’ yield is greater than the fall in the bond’s
price for a rise in he yield.
Theorem 5 : The change in the price will be less for a
percentage change in the bond’s yield if it’s coupon
rate is higher.

14. Convexity
 Bond Price and Yield are inversely related.
 The relationship is not linear.
 The degree of convexity depends on size of the bond,
years to maturity and the current market price.
Yield to Maturity
Bond Price

15. The term structure of interest rate
(Yield Curve)
Term Structure – Relationship between the yield and
years to maturity.
Expectation Theory – Anticipation of fall in inflation
rate , balanced budget, cut in fiscal deficit, recession in
economy
Liquidity Preference Theory – Investors prefer short
term than long term bonds.
Segmentation Theory- The yield is determined by the
demand for and supply of funds.

16. Duration
Duration measures the time structure of a bond and the
bond’s interest rate risk. It may be defined as the weighted
average of the length of time until the remaining cash
flows are received.
Years to Maturity- Years an investor has to wait until the
bond matures and the principal money is paid back.
Macaulay’s duration – The average time taken for all
interest coupons and the principal to be recovered.
Pv (Ct) C1 + C2 + ……. + Ct
D = Σ --------- x (t) , Pv(Ct) = ---- ----- -----
Po (1+r) (1+r)2 (1+r)t
D= Duration C= Cash flow, r = Current yield to maturity
t = Number of years Pv(Ct) = Present value of the cash flow,
Po = Sum of the present values of cash flows.

17. General Rule
 Higher the coupon rate, lower the duration and less
volatile the bond price.
 Longer the term to maturity, longer the duration and
more volatile the bond.
 Higher the yield to maturity, lower the bond duration
and bond volatility and vice versa.
 In a zero coupon bond, the bond’s term to maturity
and duration are the same.

18. Calculate the duration for bond A and bond B with 7%
and 8% coupons having a maturity period of 4 years.
The face value is Rs.1000. Both the b0nds yield 6%.
Bond A:
Year Cash Flow PvCt= Ct/(1+r)t PvCt/Po (PvCt
/Po)*t
1 70 70/(1+.06)=66.04 0.0638 0.0638
2 70 70/(1+.06)2 =62.3 0.0602 0.1204
3 70 70/(1+.06)3 =58.77 0.0568 0.1704
4 1070 1070/(1+.06)4
=847.55
0.8191 3.2764
P0 = 1034.66 D=3.6310

19. Bond B:
Year Cash Flow PvCt= Ct/(1+r)t PvCt/Po (PvCt
/Po)*t
1 80 80/(1+.06)= 75.47 0.0706 0.0706
2 80 80/(1+.06)2 = 71.2 0.0666 0.1332
3 80 80/(1+.06)3 =67.17 0.0628 0.1884
4 1080 1080/(1+.06)4 =855.46 0.8000 3.2000
P0 = 1069.3 D=3.5922

20.  Modified Duration – It can be derived by making a
small adjustments in Maculays’ duration. Modified
duration is defined as Macaulay’s duration divided by
(1+YTM).
D* = D/ (1+YTM)