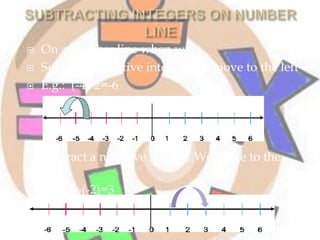
The document defines integers and their properties under addition, subtraction, multiplication, and division. It states that integers include whole numbers and their negatives, and are closed under addition and subtraction. Properties discussed include commutativity, associativity, distributivity, and operations with zero. Integers are not closed under division and division is not always commutative.

1. MADE BY:DIPIN YADAV
SUBMITTED TO:NEELU MAM

2.  Integers form a bigger collection of numbers which
contains whole numbers and negative numbers.
 The numbers _ _ _, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 _ _
_ etc are integers.
 1, 2, 3, 4, 5 _ _ _ are Positive integers.
 _ _ _-5, -4 , -3, -2, -1 are Negative integers.
 Integer ‘0’ is neither a positive nor negative
integer.
 Integer ‘0’ is less than a positive integer and
greater than negative integer.

4.  On a number line when we
 add a positive integer, we move to the right.
 E.g.: -4+2=-2
 add a negative integer, we move to left.
 E.g.: 6+(-4)=2

5.  On a number line when we
 Subtract a positive integer, We move to the left
 E.g.: (-4)-2=-6
 Subtract a negative integer, We move to the
right
 E.g.: 1-(-2)=3

6. SIGN
E.g.: 6+3=9
E.g.: -9-2= -11
greater value
E.g.: +2-4= -2
-2+4=+2

7. INTEGER ADDITIVE INVERSE
10 -10
-10 10
76 -76
-76 76
0 0

9.  ADDITION:
Integers are closed under addition. In general
for any two integers a and b, a+b is an integer.
E.g.: -2+4=2
 SUBTRACTION:
Integers are closed under subtraction. If a and b
are two integers then a-b is also an integer.
E.g.: -6-2=-8

10.  ADDITION:
This property tells us that the sum of two
integers remains the same even if the order of
integers is changed. If a and b are two integers,
then a+b = b+a
E.g.: -2+3 =3+(-2)
 SUBTRACTION:
The subtraction of two integers is not
commutative. If a and b are two integers ,then
a-b = b-a
E.g.: 4-(-6) = -6-4

11.  ADDITION:
This property tells us that that we can group integers
in a sum in any way we want and still get the same
answer. Addition is associative for integers. In
general, a+(b+c) = (a+b)+c
E.g.: 2+(3+4) = (2+3)+4 =9
 SUBTRACTION:
The subtraction of integers is not associative. In
general, a-(b-c) = (a-b)-c
E.g.: 3-(5-7) = (3-5)-7
5 = -9

12.  Multiplication of two positive integers:
If a and b are two positive integers then their product
is also a positive integer
i.e.: a x b = ab
 Multiplication of a Positive and a Negative Integer:
While multiplying a positive integer and a negative
integer, we multiply them as whole numbers and
put a minus sign(-) before the product. We thus get a
negative integer. In general, a x (-b) = -(a x b)
 Multiplication of two negative integers:
Product of two negative integers is a positive
integers. We multiply two negative integers as
whole numbers and put the positive sign before the
product. In general,
-a x -b = a x b

14.  Closure under Multiplication:
The product of two integers is an integer. Integers
are closed under multiplication. In general, a x b is
an integer.
e.g.: -2 x 2 = -4
 Commutativity of Multiplication:
The product of two integers remain the same even
if the order is changed. Multiplication is
commutative for integers. In general, a x b =b x a
e.g.: 2 x (-3) = -3 x 2

15.  Associativity of multiplication:
The product of three integers remains the same,
irrespective of their arrangements.
In general, if a, b and c are three integers, then a x (b x
c) = (a x b) x c
e.g.: -2 x (3 x 4) = (-2 x 3) x 4 = -24
 Multiplication by zero:
The product of any integer and zero is always.
In general, a x 0 = 0 x a =0
e.g.: -2 x 0 =0
 Multiplicative identity:
The product of any integer and 1 is the integer itself.
In general, a x 1 = 1 x a = a
e.g.: -5 x 1= -5

16.  Distributivity of multiplication over addition:
If a, b and c are three integers, then
a x (b+c) = a x b + a x c
e.g.: -2 x (4+5) = -2 x 4 + -2 x 5
 Distributivity of multiplication over subtraction:
If a, b and c are three integers, then
a x (b-c) = a x b - a x c
e.g.: -9 x (3-2) = -9 x 3 – (-9) x 2

17.  Division of two Positive Integers:
If a and b are two positive integers then their
quotient is also a positive integer.
e.g.: 4 ÷ 2 = 2
 Division of a positive and a negative integer:
When we divide a positive integer and a negative
integer, we divide them as whole numbers and
then put a minus sign (-) before the quotient. We,
thus, get a negative integer. In general, a÷ (-b) = (-
a) ÷ b where b = 0
 Division of two negative integers:
When we divide two negative integers, we first
divide them as two whole numbers and then put a
positive sign (+). We, thus, get a positive integer.

18.  Integers are not closed under division. In other
words if a and b are two integers, then a ÷ b may
or may not be an integer.
 Division of integers is not commutative. In other
words, if a and b are two integers, then a ÷ b = b ÷
a.
 Division by 0 is meaningless operation. In other
words for any integer a, a ÷ 0 is not defined
whereas 0 ÷ a = 0 for a = 0.
 Any integer divided by 1 give the same integer. If
a is an integer, then a ÷ 1 = a.
 For any integer a, division by -1 does not give the