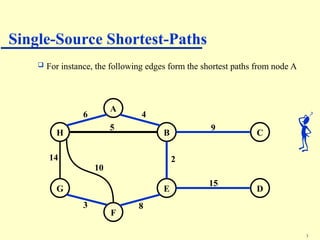
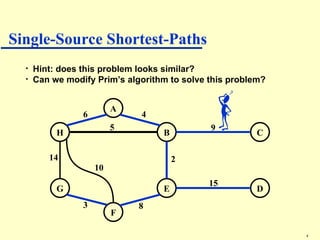
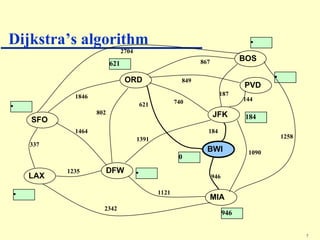
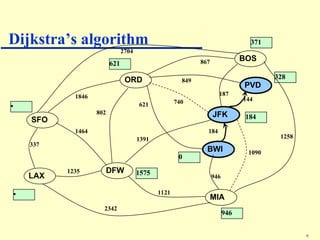
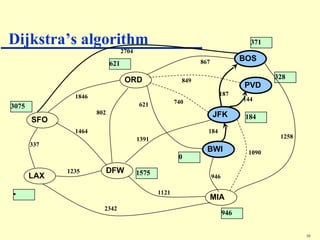
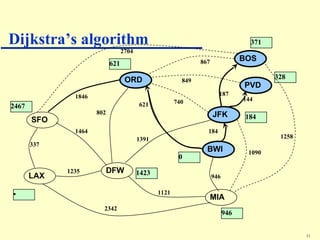
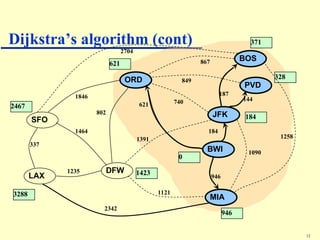
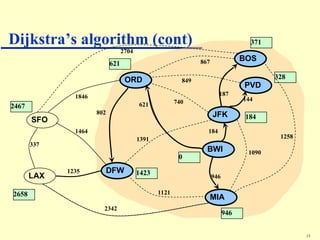
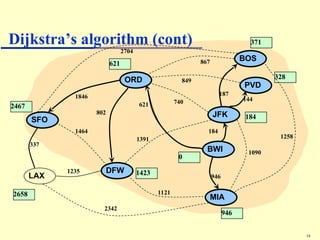
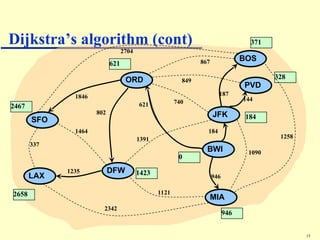
Dijkstra's algorithm addresses the single-source shortest-paths problem in connected graphs with non-negative edge weights, determining the shortest paths from a source vertex to all other vertices. The algorithm maintains a table of shortest path lengths, updates these paths iteratively using a priority queue, and has a time complexity of O((n + m) log n). It is widely applicable in various fields, such as road map applications.