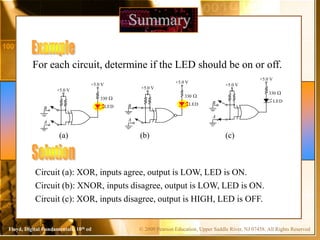
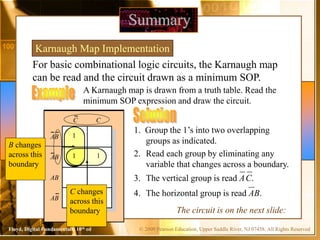
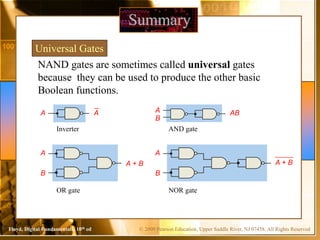
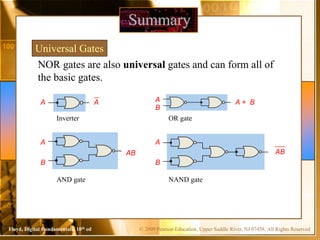
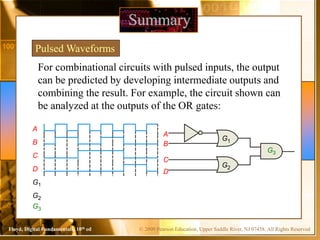
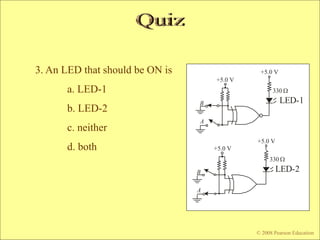
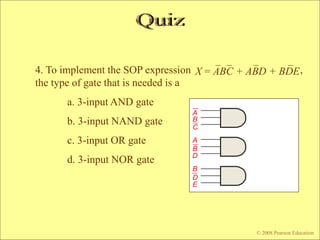
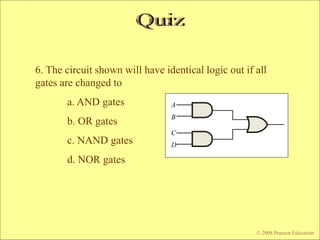
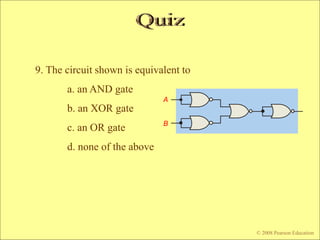
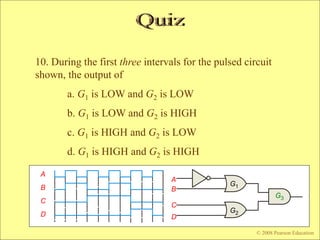
The document contains chapters from a digital fundamentals textbook covering topics such as combinational logic circuits, Karnaugh maps, universal gates, and pulsed waveforms. It provides examples of implementing sum-of-products expressions using AND-OR gates, converting circuits to NAND or NOR form, reading logic expressions from Karnaugh maps, and analyzing the output of combinational circuits with pulsed inputs. It also contains several practice problems with answers.