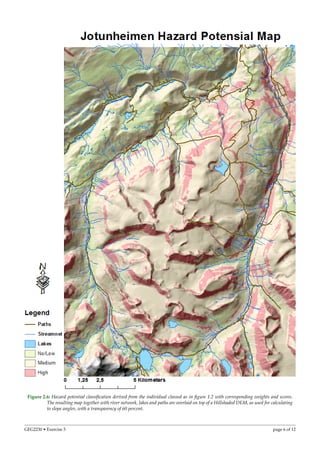
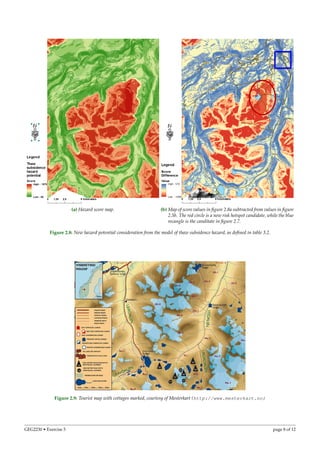
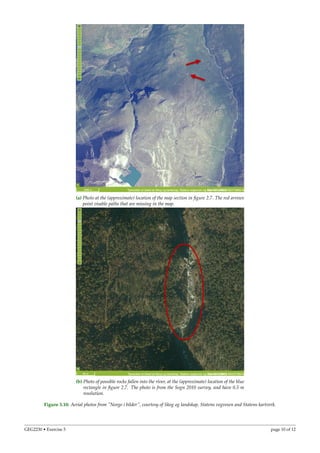
The document summarizes a multi-criteria analysis performed to identify hazard risk zones in Jotunheimen, Norway. Spatial data on slope, permafrost, sediment, and bedrock were analyzed using GIS and weighted aggregation. Hazard potential maps were produced and risk hotspots identified, including an area with paths located in high risk zones. The analysis could help prioritize preemptive measures, rescue resource allocation, and issuing of hazard warnings.

1. Assignment 2:
Multi-Criteria Analysis
Didrik Lilja, April 28, 2014

2. 1Introduction
With this report we want to identify hazard risk zones in Jotunheimen, and perform an multi-criteria (decision)
analysis (MCA/MCDA) in how these zones pose a risk. Risk in this respect is tied to vulnerability, in how likely
potential hazards could affect lifes or properties.
GIS is often recognized ‘as a decision support system involving the integration of spatially referenced data in a
problem solving environment’. On the other hand, MCDA provides a rich collection of techniques and procedures
for structuring decision problems, and designing, evaluating and prioritizing alternative decisions (Malczewski,
n.d., pp. 1).
Jotunheimen contains a national park and is a popular tourist area. To decide where and when to issue geotech-
nical hazard warnings (for instance landslide and debris flow, see (NVE, n.d.) and photo examples in figure 1.1 taken
off the same site), where to construct trekking paths, where to do preemptive measures and for allocating enough
standby rescue resources are all possible application of MCDA. By following the MCDA classification given in the
review article of MCDA application from 1994 to 2004 (Malczewski, n.d., pp. 4), our MCA application falls into
the class of having a set of uncontrollable variables or states of nature (decision environment). In our context there
are no conflicting objectives (such as land-use vs. environment protection); we will evaluate how multiple predis-
position criteria interact evaluating by means of weighted aggregation to produce a suitability map (Burrough &
McDonnel, 1998, pp. 172), suitable to identify risk hotspots.
In this report we make use of raster data input. The cell-wise representation of attribute values makes it in
general easy to perform map algebra and quantify hazard potensial at each cell of the map. The quantified number
(score) will in turn be classified into common language. Having such a map at hand enables us to make decision
analysis and identify what areas that really become a risk to humans or things we value. To start off, we calculate
the potential geotechnical hazard zones as a cartographic map, as described in the section below.
(a) Triagular-shaped landslide (b) Debris flow
Figure 1.1: Examples of geohazards, courtesy of NVE.
GEG2230 • Exercise 5 page 1 of 12

3. 1.1 Method of making a hazard potential cartographic model
Our cartographic model assumes a permafrost slope induced hazard potential. As input we use a distribution
maps for permafrost existence probability classes in conjunction bedrock lithology and sediment cover classes.
Furthermore, the terrain slope angles are an essential part of the model and thus needed. Slope angles are derived
from a raster digital elevation model (DEM) having a 50 m cell resolution.
1.1.1 Classification
Each of the inputs maps will be regarded as predisposition factors for a hazard potential, which are referred to as
parameters. The parameters will be assigned with weights Wi, while each parameter class will be assigned with
scores Sj representing the severity of a hazard occurrence. Suggested classes are given in the table 1.1 below. As
a constraint is the sum of weights set to 100, which gives a good notion of their relative importance (ranking).
Notice the consequence that the max potential of parameter is then 100 (if the rest have weight equal to 0), but
does nevertheless not correspond to certainty. The scores distribution however does not have the similar constraint
imposed.
Since we have raster data at hand, no classification meta data is available other than an class raster ID. This
means that each raster cell belongs to a unique class, represented by a class ID attribute assigned at each cell. A
reclassification from provided class ID is consequently necessary. We however would want to have classification
with weights assigned to each class. To accomplish this we have performed a reclassification which redefine the
class IDs to correspond to the weight values. The ArcGIS flow chart model in figure 1.3 implements this.
Remark: The weight values may not be unique, thus original class divisions may vanish at congruent weights with
this method. It should however not cause any problems for our purpose.
Model parameter Parameter classes Class ID Class scores Sj Parameter weights Wi
Slope angle (j = 1): 0°- 15° - 0 (e) 35
15°- 30° - 7
30°- 45° - 10
45°- 75° - 7
Permafrost existence (j = 2): Probable permafrost 1 10 20
Possible permafrost 2 8
No permafrost 3 1
Sediment cover (j = 3): Thick moraine cover 11 10 40
Thin moraine cover 12 5
Fluvial/glasio-fl 50 2
In-situ weathering 130 5
Talus 81 5
Organic 90 5
Exposed bedrock 20 0 (e)
Bedrock lithology (j = 4): Competent massive lith. 1 2 5
Competent lith., joined 2 5
Non-competent lith. 3 10
Table 1.1: Weighted mutual rank for potential of geotechnical hazards in the Jotunheimen area, along with a score value of impact severity
of each parameter class.
GEG2230 • Exercise 5 page 2 of 12

4. (a) Distribution of permafrost classes. (b) Distribution of sediment classes.
(c) Distribution of bedrock classes. (d) Hillshaded DEM of Jotunheimen with 1.5 as z factor.
Figure 1.2: Spatial distribution of classes for each model parameter.
GEG2230 • Exercise 5 page 3 of 12

5. 1.1.2 Map algebra calculations
Our calculation will be based on the following formula:
Sp =


j
WjSj

 · e, (1.1)
applied to each raster cell, where e = 0 for some classes (here: ≡ Sj = 0) and otherwise e = 1. The "support
function" (boolean operator) e represents in principle a hard criteria for the presence of a hazard potential, while
the other weights represent soft criteria. We notice that the j denotes the parameter index, but it also applies to the
uniquely assigned class score index at each parameter. To implement the "support function" e one can set related
areas as NoData, which is treated so that the output in also is becomes NoData.
Remark: The above-mentioned implementation was unfortunately not done in this report, but can still be justified as
being on the conservative side in terms of risk as actual NoData is distinguished out and not automatically regarded
as safe.
Remark: When performing numerical calculations, errors stemming from e.g. raster data input propagate though
the calculations, see for instance (Burrough & McDonnel, 1998, pp. 228). Our calculation is fairly simple as there are
not many calculation steps involved, thus we do not anticipate any large numerical error contribution, and probably
insignificant compared to parameter uncertainties.
Figure 1.3: Flow chart for calculating the debris flow hazard zones in ArcGIS.
Figure 1.4: Raster calculation expression in ArcGIS.
GEG2230 • Exercise 5 page 4 of 12

6. 2Results
Figure 2.5a shows the distribution of calculated slope angles, classified into three categories (three different score
values). Then the map algebra operation in combining all parameters can be performed (figure 1.4) with a resulting
hazard score map as displayed in figure 1.2.
(a) Derived slope angles (ArcGIS Resource Center, 2011), based on
the same DEM as used in figure 1.2d.
(b) Calculated scores for hazard potential, based on derived slope an-
gles (figure 2.5a) and distribution of permafrost classes (figure
1.2a), sediment cover classes (figure 1.2b) and bedrock lithology
classes (figure 1.2c), along with the given weights and scores.
Figure 2.5
The hazard scores calculated can be simplified to understandable language for common people, by classifying
the scores. A well-established strategy could in principle be utilized in characterizing how the scores actually relates
to real risk, e.g. by comparing with recorded accidents. For remaining part of this report we have simply re-classified
into three categories namely no/low, medium and high potential zones. The resulting cartographic map is overlaid
transparently on top of the Hillshaded DEM, together with river network, lakes and paths/roads (from now on
only referred to paths), making it better for assessing the results as more topography details can be recognized, see
figure 2.6. Similarly, as a warning tools it is easier to use and understand. Contour lines can also be used, such as in
the map section shown in figure 2.7, to get an even better understanding of local slope steepness.
GEG2230 • Exercise 5 page 5 of 12

7. Figure 2.6: Hazard potential classification derived from the individual classed as in figure 1.2 with corresponding weights and scores.
The resulting map together with river network, lakes and paths are overlaid on top of a Hillshaded DEM, as used for calculating
to slope angles, with a transparency of 60 percent.
GEG2230 • Exercise 5 page 6 of 12

8. Figure 2.7: North-east section of hazard potential areas from figure 2.6. The blue square indicated a risk hot spot candidate. The blue
arrows points at possibly missing paths in the map, as can be seen in figure 3.10.
By looking at figure 2.6 we can see that trekking paths are mostly outside of the high potential hazard zones
(light red map color), but not everywhere, especially in valleys with steep surrounding hills. Probably permafrost
existence seems in comparison to have few paths, which might be one explanation. Settlements/properties are
rare in national parks and has therefor been given little attention in this report. There are however few cottages
as indicated in the tourist map in figure 2.9, which in comparison looks to be in safe areas. One particular area is
indicated in the red rectangle in figure 2.7 as a candidate for being a risk hot spot since several paths are located
inside or close vicinity the light red zones. This is an area dominated by thick moraine cover, with a mix of gentle
and steep slopes and no permafrost. Furthermore, missing paths in the map has identified within the hotspot, as
shown in figure 3.10 in the next section, and poses a risk for decision makers in where to pay attention when making
their choices. As an example such inadequacy is illustrated at the blue arrows inside the risk hotspot.
An alternative model consider thaw subsidence hazard, for which altered weighting and scores have been used,
but still modelled with the same parameters. The resulting hazard score map in figure 2.8a has significant differ-
ences, particular since permafrost existence is given more significance. Identifying risk hotspots could for instance
take this map into consideration as well. The map does not introduce much more risk for our risk hotspot candidate
in figure 2.7, but introduces however more risk into the permafrost area and where a few path are found, see figure
2.8.
GEG2230 • Exercise 5 page 7 of 12

9. (a) Hazard score map. (b) Map of score values in figure 2.8a subtracted from values in figure
2.5b. The red circle is a new risk hotspot candidate, while the blue
recangle is the canditate in figure 2.7.
Figure 2.8: New hazard potential consideration from the model of thaw subsidence hazard, as defined in table 3.2.
Figure 2.9: Tourist map with cottages marked, courtesy of Mesterkart (http://www.mesterkart.no)
GEG2230 • Exercise 5 page 8 of 12

10. 3Discussions and Summary
One should have in mind the weighted parameter importance. The weighing direct us in where look for risk
hotspots or aid us in reiterating the calculations with different weights in order to improve the model. Now, we
have assigned the sediment cover with the highest weight (40) and thick moraine cover has the highest score (10)
within the parameter, so this class might be of particular interest. Using the hillshaded DEM we see correlation
between steep slopes and hazard zones, but also with thick moraine cover distribution and permafrost existence.
The bedrock lithology is not easily recognized in the hazard potential map, and is classified to be fairly constant
over most of the areas where other parameters come into play. One may because of this question the need for this
parameter in the Jotunheimen area.
In term of risk assessment, it usually safer to be conservative in the risk prediction. Similarly, it is also important
to check that all susceptible areas are taken into consideration. To do so, field observations, aerial photos and
historical information and existing maps serve as information for comparing/verifying our the prediction with. In
this section we have chosen to present aerial photos from the particular map area in figure 2.7, albeit other areas
might deserve particular attention as well. Ideally, a model of nature processes should be able to predict historically
known occurrences of hazards. This is not evaluated in this report, but generally recommended.
Figure 3.10b indicates that the red area indeed might be a dangerous area for people, which support our model.
Figure 3.10a on the other hand point at unmapped paths, which also deserves attention as these lay in red high
potential areas, and thus reduce the validity of our map (path information), although not the model itself.
3.1 Sensitivity to parameter variations
The weights and scores need an justification (calibration), either empirically or as a physically modelled process.
Better calibration is obviously of interest, but this task of achieving this out of scope in this report. Yet, an imposed
variation of parameters might still provide us with the model dynamics. Say if the model is significantly more sen-
sitive to a particular parameter in terms of variation (perturbation) than others, then a refinement of classes might
be a possible solution to reduce the sensitivity. The mutual ranking could also been done differently, like analytical
hierarchy process (AHP) (Saaty, 2008) which ranks mutually pair-wise instead of an ordinal overall ranking we
have used. Another way is to divide the analysis into subcategories of hazard type with different set of parameters.
3.2 Temporal considerations
Yearly input variations might highly affect the comparison to aerial pictures. In an actual real-life MCA application
one should have this in mind, besides that susceptible areas might change as well, such as whenever new paths are
developed or new settlements build.
On the other hand, the parameters for risk are fairly independent of seasonal variations and the model can per-
ceive us to believe that seasonal variations are not a factor, which is clearly questionable. By incorporating probable
permafrost existence may to some extent incorporate temporal variations in the sense of temporal statical average.
An enhanced model prediction for landslides could as a suggestion incorporate thaw processes and precipitation
levels as model parameters to cope for seasonal variations more directly from measurements and weather forecasts.
GEG2230 • Exercise 5 page 9 of 12

11. (a) Photo at the (approximate) location of the map section in figure 2.7. The red arrows
point visable paths that are missing in the map.
(b) Photo of possible rocks fallen into the river, at the (approximate) location of the blue
rectangle in figure 2.7. The photo is from the Sogn 2010 survey, and have 0.5 m
resolution.
Figure 3.10: Aerial photos from ”Norge i bilder”, courtesy of Skog og landskap, Statens vegvesen and Statens kartverk.
GEG2230 • Exercise 5 page 10 of 12

12. Model parameters Parameter classes Class ID Class scores Sj Parameter weights Wi
Slope angle (j = 1): 0°- 15° - 10 25
15°- 30° - 5
30°- 45° - 0 (e)
45°- 75° - 0 (e)
Permafrost existence (j = 2): Probable permafrost 1 19 50
Possible permafrost 2 8
No permafrost 3 0 (e)
Sediment cover (j = 3): Thick moraine cover 11 10 25
Thin moraine cover 12 3
Fluvial/glasio-fl 50 2
In-situ weathering 130 7
Talus 81 2
Organic 90 10
Exposed bedrock 20 0 (e)
Bedrock lithology (j = 4): Competent massive lith. 1 0 (e) 0
Competent lith., joined 2 2
Non-competent lith. 3 5
Table 3.2: Table 1.1 with revised weights and scores to representing thaw subsidence hazard potential.
3.3 Spatial considerations
Landslide can developed into a triangular shape as in figure 1.1a A wider fuzzy set representation (more gradual)
along the slopes downstream can the risk representation map.
The 50 m resolution might be to coarse for our purpose. We have looked at map section with a 1:50.000 scale.
At this scale the raster cells become clearly visible, but for general use bigger scale, e.g. 1:10.000, might be more
suitable. Debris flow smaller than 50 m wide can do much harm, and sudden changes in topography, particularly
relevant for terrain slopes (which are weighted 35 percent importance), might not be captured at the resolution.
3.4 Conclusion
This report have shown an example of MCA in going though the steps of making a hazard risk map, with reasonable
agreement with the input data. Trekking paths have been of particular interest when looking for risk hotspots.
Candidates for risk hotspots have been identified, but has also been seen in relation to model parameter variation.
GEG2230 • Exercise 5 page 11 of 12

13. References
ArcGIS Resource Center. (2011). Slope (Spatial Analyst). Retrieved April, 2014, from http://help.arcgis.com/
en/arcgisdesktop/10.0/help/index.html#//009z000000v2000000.htm
Burrough, P. A., & McDonnel, R. A. (1998). Principles of Geographical Information Systems. Oxford University Press,
New York.
Malczewski, J. (n.d.). A new procedure for gridding elevation and stream line data with automatic removal of
spurious pits. International Journal of Geographical Information Science, 20.
NVE. (n.d.). Jordskred og flomskred. Retrieved April, 2014, from http://varsom.no/Global/Faktaark/Fakta
%205-13%20Jord%20og%20flom.pdf
Saaty, T. L. (2008). Decision making with the analytic hierarchy process [Journal Article]. Int. J. Services Sci-
ences, 1, 83-98. Retrieved from http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1
.409.3124&rep=rep1&type=pdf
GEG2230 • Exercise 5 page 12 of 12