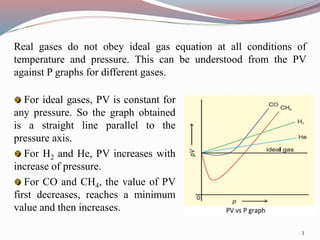
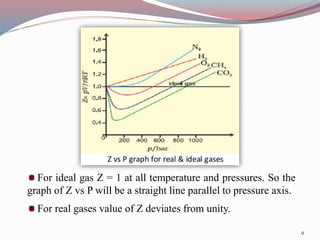
Real gases deviate from ideal gas behavior at high pressures and low temperatures due to the assumptions of negligible molecular volume and no intermolecular forces being incorrect in those conditions. Van der Waals proposed an equation to account for these deviations that includes pressure and volume correction terms related to intermolecular attractive forces and molecular size. The compressibility factor Z, which is the ratio of PV to nRT, can quantify this deviation from ideal behavior for real gases as it equals 1 for ideal gases but varies from 1 for real gases.

1. Behaviour of real gases :
deviation from ideal behaviour
Presented by,
Vidya K C
Roll No. :36
Reg.No. :DD16EDPS06
Physical Science
Presented on 25-10-2017 1

2. CONTENTS
Introduction
Reasons for deviation from ideal behaviour
van der Waal’s equation
Significance of van der Waal’s constants
Compressibility factor
2

3. Real gases do not obey ideal gas equation at all conditions of
temperature and pressure. This can be understood from the PV
against P graphs for different gases.
For ideal gases, PV is constant for
any pressure. So the graph obtained
is a straight line parallel to the
pressure axis.
For H2 and He, PV increases with
increase of pressure.
For CO and CH4, the value of PV
first decreases, reaches a minimum
value and then increases.
3

4. Reasons for deviation from ideal behaviour
This can be attributed to two wrong assumptions of kinetic
theory of gases.
They are:
1. The actual volume of the molecules is negligible
compared to the volume of the gas.
2. There is no force of attraction between the gas
particles.
These two assumptions become wrong at high pressure and
low temperature.
4

5. real gases obey ideal gas equation at low
pressure and high temperature.
Or
real gases deviate from ideal behaviour at high
pressure and low temperature.
5

6. van der Waal proposed an equation, which is applicable to
real gases.
(P + n2a/V2) (V- nb) = nRT
Where,
P is the pressure of the gas,
V is the volume,
R is the universal gas constant,
T is the absolute temperature,
n is the no. of moles,
‘a’ and ‘b’ are called van der Wall’s constants.
The term n2a/V2 is related to pressure correction and term ‘nb’
is related to volume correction.
van der Waal’s equation
6

7. Significance of van der Waal’s constants
‘a’ is a measure of magnitude of inter molecular attractive
forces within the gas and its unit is L2atm mol-2
‘b’ is related to the volume of the particles and unit of ‘b’
is L mol-1.
7

8. Compressibility factor Z
The deviation from ideal behaviour can be measured in terms
of compressibility factor Z, which is the ratio of product PV
and nRT.
Mathematically,
Z = PV/nRT
For ideal gas Z = 1 at all temperature and pressures. So the
graph of Z vs P will be a straight line parallel to pressure axis.
For real gases value of Z deviates from unity.
8

9. For ideal gas Z = 1 at all temperature and pressures. So the
graph of Z vs P will be a straight line parallel to pressure axis.
For real gases value of Z deviates from unity.
9

10. THANK YOU
10