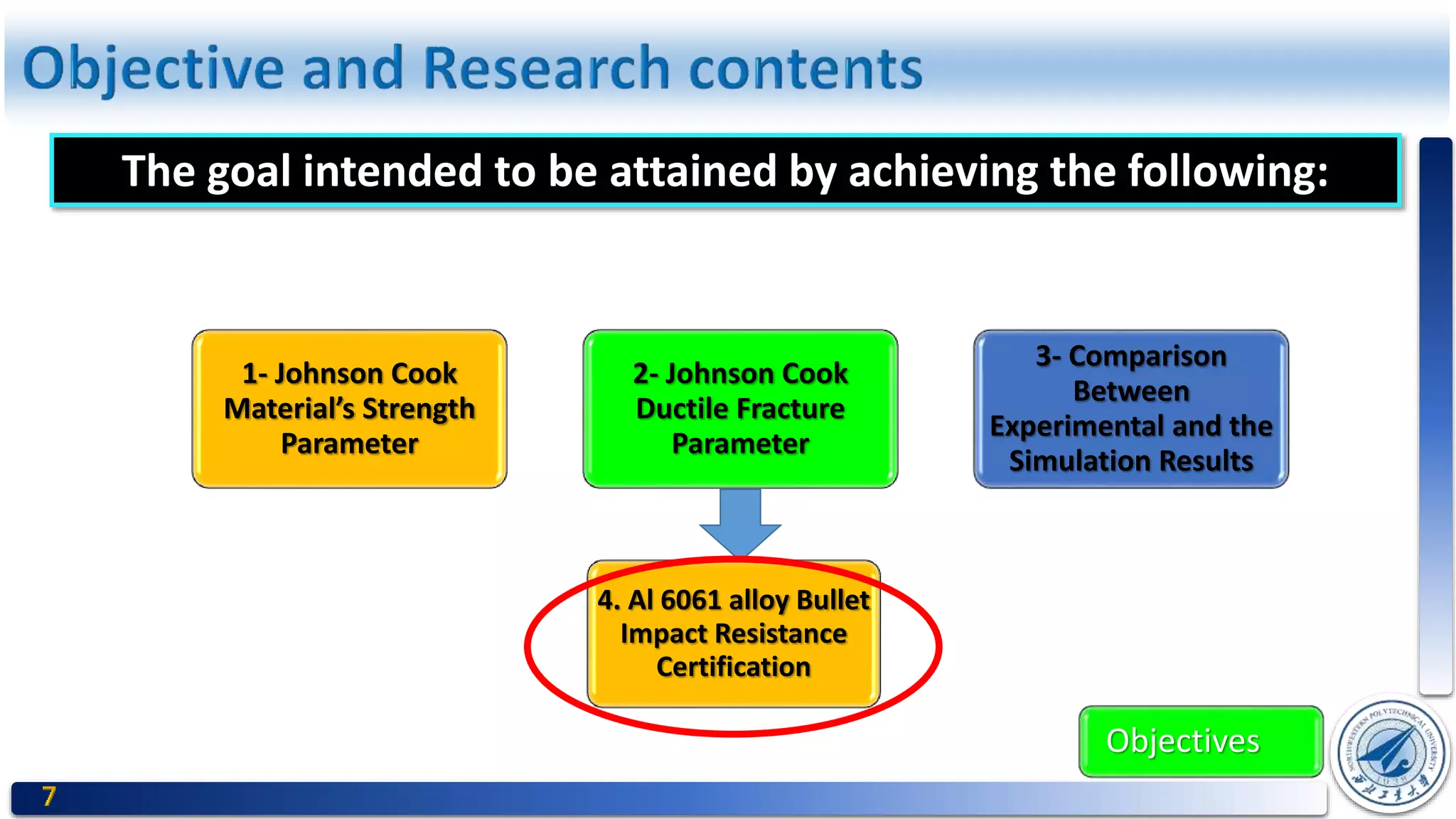
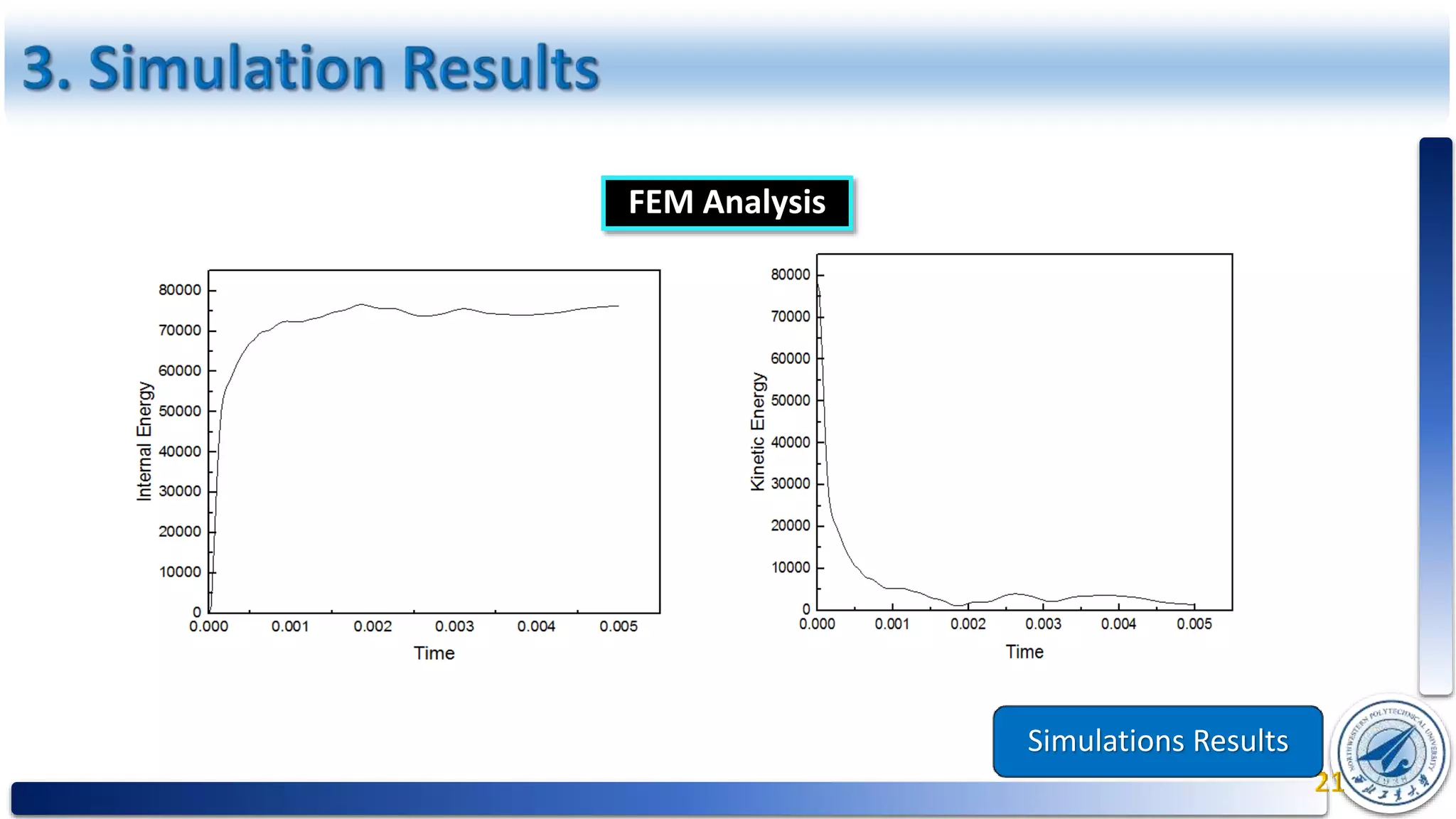
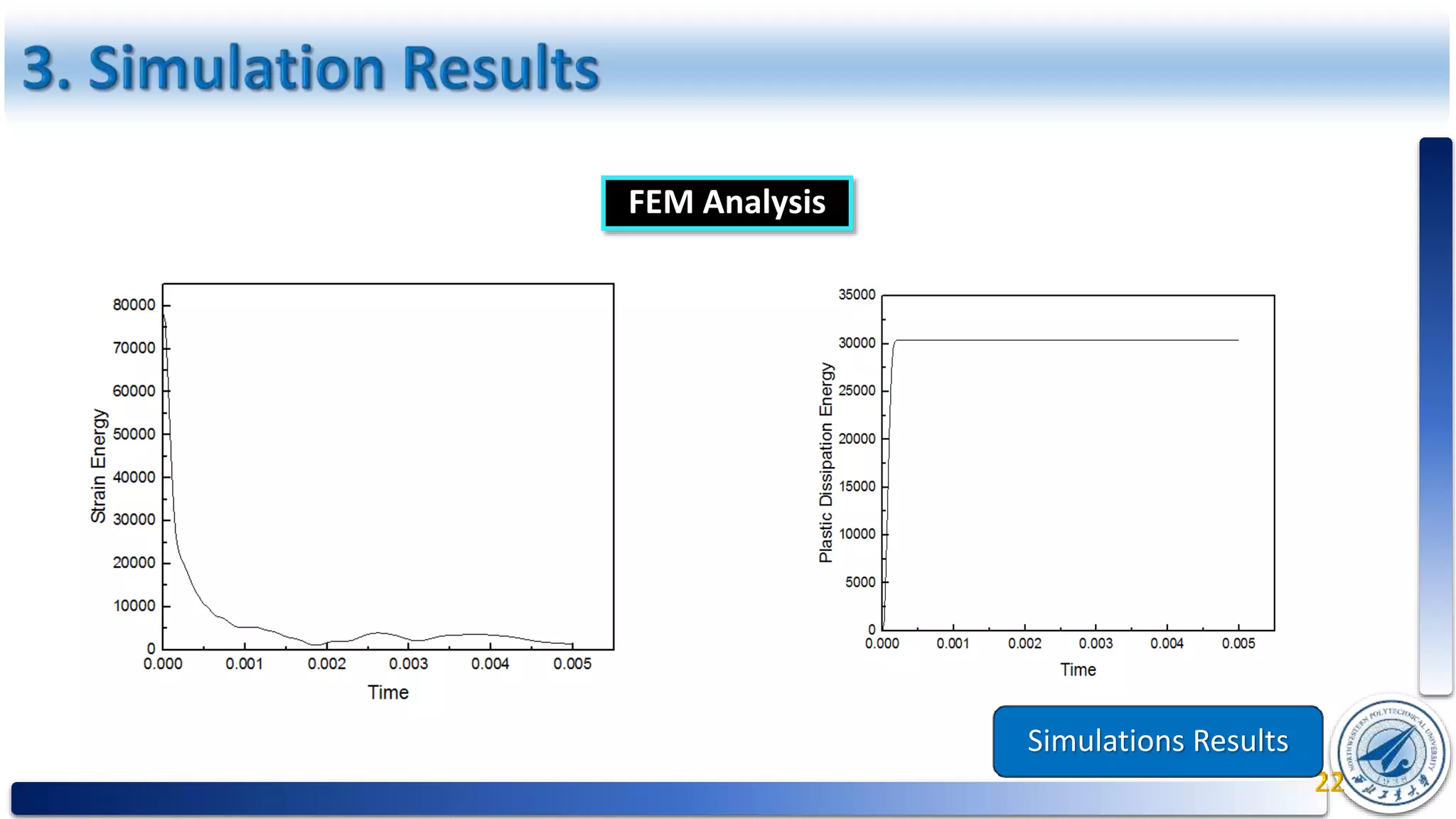
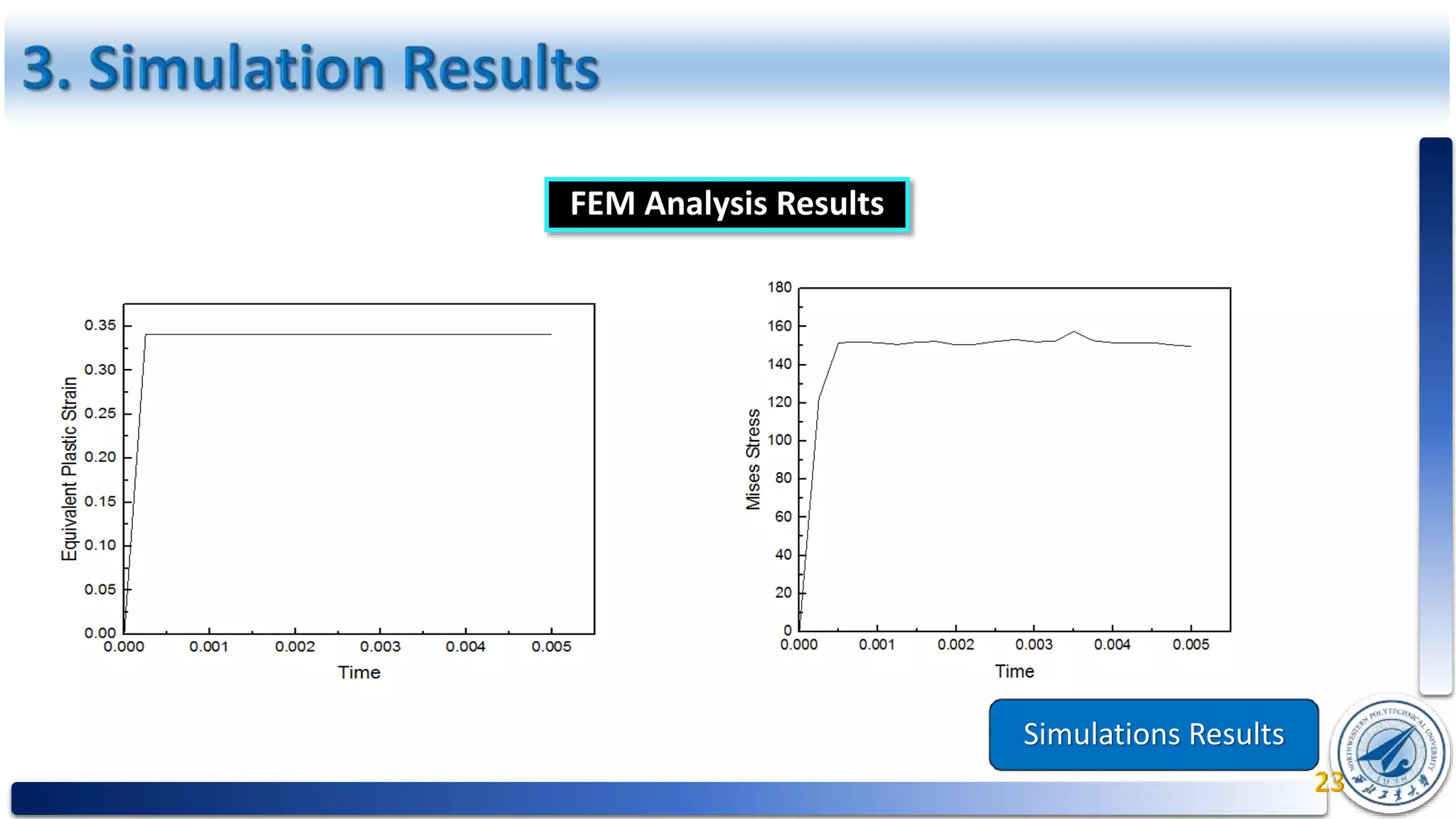
This document presents a study on determining the Johnson-Cook material strength and fracture parameters and their application to assess the bullet impact resistance of the AL 6061 alloy. It includes a literature review, methodology for experimentation, and analysis of results involving quasi-static and dynamic tensile tests across various temperatures and strain rates. The study aims to fit equations for material behavior under extreme conditions, providing constants necessary for the Johnson-Cook model to predict performance under bullet impact.

1. School of Aeronautics
Determination of Johnson Cook Material’s Strength
Parameter, Fracture Parameter, And Application to
Bullet Impact Resistance of Al 6061 alloy.
Major: Solid Mechanics
By
Bharosh Kumar Yadav
MSc. Student
Supervisor : Prof. Suo Tao(索涛)
1

2. 1- Literature Review
2- Objectives and Research Content
3- Methodology
4- Result and Discussions

3. Review
[1] W. H. C. Gordon R. Johnson, "A constitutive model and data for metals
Subjected to large strains, high strain rates and high temperatures.," Proc. 7th Int.
Symposium on Ballistics, Hague, Netherlands, April 1983, pp 541-548.
William H. Cook and Gordon R. Johnson, presents a constitutive model and data for materials subjected to large
high strain rates and high temperatures. The model for the von Mises flow stress, σ, is expressed as
𝝈 = 𝑨 + 𝑩 𝜺 𝒑 𝒏
𝟏 + 𝑪 𝐥𝐨𝐠 𝜺∗
(𝟏 − (𝑻∗
) 𝒎
) (1)
Where A, B, C, n and m are material constants, and are determined from an empirical fit of flow stress (as a function of
strain, strain rate and temperature) to Equation (1).
Where, ɛ 𝒑
= the equivalent plastic strain, ε∗
= ε 𝜀0is the dimensionless plastic strain rate for 𝜀0 = 1 s−1
(reference strain-
rate).
And T∗m
= ((Ttest − Troom) (Tmelt − Troom))m
is non-dimensional homologous temperature, where T is the absolute
temperature, Troom is the room temperature, and Tmelt is the material melting temperature.
The first bracket in Equation (1) gives the isothermal stress as a function of strain for 𝜀0 = 1s−1
(reference strain-rate for
convenience). The second bracket includes the strain rate effect and third bracket accounts for the thermal effects.

4. Review
The basic form of the fracture model developed was first presented in Ref. [2] The damage to an element is
defined
𝑫 = 𝜮
𝜟𝜺
𝜺 𝒇 (2)
where 𝜟𝜺 is the increment of equivalent plastic strain which occurs during an integration cycle, and 𝜺 𝒇
is the equivalent
strain to fracture, under the current conditions of strain rate, temperature, pressure and equivalent stress. Fracture is
then allowed to occur when D = 1.0. The general expression for the strain at fracture is given by
𝜺 𝒇
= 𝑫 𝟏 + 𝑫 𝟐 𝒆𝒙𝒑𝑫 𝟑 𝝈∗
𝟏 + 𝑫 𝟒 𝒍𝒐𝒈 𝜺∗ 𝟏 + 𝑫 𝟓 𝑻∗
(3)
for constant values of the variables (σ∗
, ε∗, T∗
) and for σ∗
≤ 1.5. The dimensionless pressure-stress ratio is defined as σ∗
=
σ 𝑚 σ where σ 𝑚 is the average of the three normal stresses and σ is the Von Mises equivalent stress. The dimensional
strain rate, ε∗, and homologous temperature, T∗
, are identical to those used in the strength model of equation (1).
The parameter 𝑫 𝟏, 𝑫 𝟐, 𝑫 𝟑, 𝑫 𝟒&𝑫 𝟓 are constants.
[2] G. R. Johnson, "Material Characterization for Computations Involving Severe Dynamic
Loading.," Proc. Army Symp. on Solid Mechanics, 1980, Work in Progress, Cape Cod, Mass., vol.
pp. 62-67., (Sept. 1980).

5. Review
The five constants are 𝑫 𝟏 … . 𝑫 𝟓 , The expression in the first set of brackets follows the form presented by Hancock and
Mackenzie [3]. It essentially says that the strain of fracture decreases as the hydrostatic tension, σ 𝑚, increases. The
expression in the second set of brackets represents the effect of strain rate, and that in the third set of brackets represents
the effect of temperature.
Plastic Flow And The Stress-State
Since, this fracture model is based on fracture strains at constant σ∗
, 𝜀∗
, and T∗
, and it is accurate under constant
conditions to the extent that the equivalent stress, σ, equivalent strain, 𝜺, and equivalent strain rate, 𝜀∗
, can represent the
more complicated stress and strain relationships [4].
σ =
1
2
[ σ1 − σ2
2 + σ2 − σ3
2 + (σ3−σ1)2] (4)
ε =
2
9
[ ε1 − ε2
2 + ε2 − ε3
2 + ε3 − ε1
2] (5)
𝜀 = ∑ 𝜀∆𝑡 6
Both Equivalent effective plastic strain and Equivalent effective stress are unaffected by a third important , the mean stress
σ 𝑚 =
1
3
(𝜎1 + 𝜎2 + 𝜎3) (7)
Which may, however, be combined with σ in to a single non-dimensional parameter σ 𝑚 σ which characterizes a stress-
state and of its “TRI-AXIALITY”.
[3] J. W. H. a. A. C. Mackenzie, "On the mechanisms of ductile failure in high-strength steels subjected to multi-axial stress-states.," Journal of the Mechanics
and Physics of Solids, 24, 147-169., (1976).
[4] W. H. C. Gordon R. Johnson, "Fracture Characteristics of the three metals subjected to various strains, Strain
rates, Temperatures and Pressures.," Engineering Fracture Mechanics Vol. 21, No. 1, pp.31-48, (1985).

6. Review
1- Radial
2- Hoop
3- Axial
[6] Chen Zhong Fu. CHEN Gang*, XU Wei-Fang, CH EN Yong-Mei, HUANG Xi-Cheng, "45钢的J-C损伤失效参量研
究陈刚," China Academic Journal Electronic Publishing House, vol. 27, No.2, (March 2007).
[5] P. W. Bridgman, "Studies in Large Plastic Flow and Fracture.," McGraw-Hill, New York, (1952).
(A discussion of the applicability of BRIDGMAN’S (1952) analysis to pre-notched specimens has been given by EARL and BROWN (1976)[5]). The main feature
of their analysis state that equivalent effective plastic strain remain constant across the mean cross-section, but the RADIAL, HOOP and AXIAL stresses (σr,
σθ, and σz, resp.) vary across the section as shown in Fig. 1. The value of σ 𝑚 σ = 𝜎∗
rises from 1/3 at the surface to a maximum value on the axis of the
specimen, and (σ 𝑚 σ) = -(𝜎∗
) =
1
3
+ log(1 +
𝑎
2𝑅
) at the axial line behind in the main equation of ”Johnson Cook Fracture Model Equation”[6].
Where, R is the profile radius of the circumferential notch and d is the radius of the minimum cross-section.
Thus, the stress-state is defined by the geometry of the specimen, and effective plastic strain is 𝜀 𝑝
= 2 log( 𝑑0 𝑑).
Where, 𝑑0 is the initial value of d.

7. 1- Johnson Cook
Material’s Strength
Parameter
2- Johnson Cook
Ductile Fracture
Parameter
3- Comparison
Between
Experimental and the
Simulation Results
The goal intended to be attained by achieving the following:
4. Al 6061 alloy Bullet
Impact Resistance
Certification
Objectives

8. 1. Geometry of Experimental Specimen
2. Experimental Implementation Machines
Methodology

9. Methodology
1- Johnson Cook
Material’s Strength
Parameter
2- Johnson Cook
Ductile Fracture
Parameter

10. Methodology
3- Bullet Impact

11. 1. Johnson Cook
Al 6061 alloy
Strength Model
Constants
2. Johnson Cook
Al 6061 alloy
Fracture Model
Constants
3. Bullet Ballistic
Impacts on
Al 6061 alloy
5. Analysis

12. 1. Determination of A, B, and n in the Johnson Cook Constitutive Equation
)𝝈 = 𝑨 + 𝑩 𝜺 𝒑 𝒏
𝟏 + 𝑪 𝐥𝐨𝐠 𝜺∗
(𝟏 − )𝑻∗ 𝒎
(𝟏
Experimental Condition: Quasi-Static experimental tests of smooth specimen whose radius 5.0mm for tensile tests were
performed at reference strain-rate ε 1 × 10−3
s−1
under three different temperatures, room temperature (200
C), and
high temperature 1000C and 2000C respectively performed for determination of A, B, and n.
Under this conditions, the Johnson-Cook Model Equation (1) becomes,
𝛔 = 𝐀 + 𝐁 𝛆 𝐩 𝐧
SN Johnson-Cook Strength Parameter Average obtained fitted values
1 A 318
2 B 395
3 n 0.73707

13. 2. Determination of C in the Johnson Cook Constitutive Equation
Experimental Condition: Tension experiment of smooth specimen whose dimension (size) of the specimen Φ3˟5mm were sized
to performed dynamic experiment at reference temperature (room temperature) at 200
C at three different strain rate 𝜀:
103/s, 2 × 103/s 𝑎𝑛𝑑 3 × 103/s respectively for determination of Johnson Cook Strength parameter “C”. Under this
conditions, the Johnson-Cook Model Equation (1) becomes,
𝛔
𝐀
= 𝟏 + 𝐂 𝐥𝐨𝐠 𝛆∗
SN “C” Chosen any one results from any Temperatures. Average Fitted Values of “C”
1. 200C( 𝜀: 103,2 × 103 𝑎𝑛𝑑 3 × 103). C 𝐴𝑣𝑒𝑟𝑎𝑔𝑒 =0.00819
2. 1000C( 𝜀: 103,2 × 103 𝑎𝑛𝑑 3 × 103) C 𝐴𝑣𝑒𝑟𝑎𝑔𝑒=0.00872
3. 2000
C( 𝜀: 103
,2 × 103
𝑎𝑛𝑑 3 × 103
) C 𝐴𝑣𝑒𝑟𝑎𝑔𝑒=0.01224

14. 3. Determination of m in the Johnson Cook Constitutive Equation
Experimental Condition: Quasi-Static experimental tests of smooth specimen whose radius 5.0mm for tensile tests were
performed at reference strain-rate ε 1 × 10−3
s−1
under three different temperatures, room temperature (200
C), and
high temperature 1000C and 2000C respectively. As, the average values of A has been already calculated depicted in
Table
Under this conditions, the Johnson-Cook Model Equation (1) becomes,
𝝈
𝑨
= 𝟏 − 𝑻∗𝒎
SN Experimental
Temperatures.
Experimental
True Plastic Stress
(σ)
Average Experimental Fitted Values of
“A”
σ/A
1. 200C 365 317.66 1.1490
2. 1000
C 315 317.66 0.9916
3. 2000
C 282 317.66 0.8877

15. Johnson-Cook strength model constants for Al 6061 alloy
Constant A B n C m
Al6061 318.22599 395.36869 0.73707 0.01224 1.77019

16. 𝐃 𝟏, 𝐃 𝟐, 𝐃 𝟑
1. Determination of Johnson Cook Ductile Fracture Parameter 𝐃 𝟏, 𝐃 𝟐, 𝐚𝐧𝐝 𝐃 𝟑
Experimental conditions: Constants D1, D2, and D3 was determined by performing Quasi-Static tensile tests of constant strain-
rate ( 𝜀) 1 × 10−3
/s on notched specimens whose notched radius are 1.5mm, 2.0mm and 2.5mm, without notched
specimen of radius 5.0mm and Torsion specimen of radius 5.7mm and its length ≅14mm respectively at constant room
temperature (200
C). After obtaining data of the stress triaxiality state of stress for each tensile of both notched-without
notched and torsion experimental data, the fracture strain (εf
) Vs stress triaxial state of stress (σ∗
) is curve fitted used to
determine parameters of D1, D2, and D3. Under this state, equation (2) becomes,
𝜺 𝒇 = 𝑫 𝟏 + 𝑫 𝟐 𝐞𝐱𝐩𝑫 𝟑 𝝈∗
𝜺 𝒇 = 𝑫 𝟏 + 𝑫 𝟐 𝐞𝐱𝐩(𝑫 𝟑 𝝈∗) 𝟏 + 𝑫 𝟒 𝒍𝒐𝒈 𝜺∗ 𝟏 + 𝑫 𝟓 𝑻∗ (2)
S
N
Johnson-Cook Failure Parameter Average obtained fitted values
1 D1 0.51896
2 D2 1.98319
3 D3 6.80328

17. 𝐃 𝟒
2. Determination of Johnson Cook Ductile Fracture Parameter 𝐃 𝟒
Experimental conditions: Constants D4 was determined by performing dynamic tensile test under room temperature (200C) at
three strain rates ( 𝜀) 1 × 103
/s, 2× 103
/s, and 3 × 103
/s respectively. After obtaining data of the fracture strain at
different test strain rate ( 𝜀): 1 × 103/s, 2× 103/s, and 3 × 103/s respectively was curve fitted; failure strain (εf) Vs test
strain rates ( 𝜀) to determine fitting parameters of D4.
Under this state, equation (2) becomes
𝜺 𝒇 = 𝟎. 𝟓𝟏𝟖𝟗𝟔 + 𝟏. 𝟗𝟖𝟑𝟏𝟗 ∗ 𝐞𝐱𝐩(𝟔. 𝟖𝟎𝟑𝟐𝟖 ∗ (− 𝟏 𝟑) 𝟏 + 𝑫 𝟒 𝒍𝒐𝒈 𝜺∗
𝜺 𝒇 = 𝑫 𝟏 + 𝑫 𝟐 𝐞𝐱𝐩(𝑫 𝟑 𝝈∗) 𝟏 + 𝑫 𝟒 𝒍𝒐𝒈 𝜺∗ 𝟏 + 𝑫 𝟓 𝑻∗ (2)
SN Johnson-Cook
Failure Parameter
Average obtained fitted
values
1 D4 -0.07243

18. 𝐃 𝟓
3. Determination of Johnson Cook Ductile Fracture Parameter 𝐃 𝟓
Experimental conditions: Constants D5 was determined by performing dynamic tensile test under reference strain (ε) rate at
three different temperatures like 200
C, 1000
C, and 2000
C respectively. After obtaining the data of fracture strain at
different test temperatures was curve fitted; failure strain (εf
) Vs Temperatures(T) to determine fitting parameters of D5.
Table
𝜺 𝒇 = 𝑫 𝟏 + 𝑫 𝟐 𝐞𝐱𝐩(𝑫 𝟑 𝝈∗) 𝟏 + 𝑫 𝟒 𝒍𝒐𝒈 𝜺∗ 𝟏 + 𝑫 𝟓 𝑻∗ (2)
SN Failure Strain (εf
) Temperatures
1. 0.794193717
0.526382105
0.794139717
200C
1. 0.713349888
0.867729165
0.747932882
1000C
1. 0.892574205
0.867729165
0.818946259
2000C
SN Johnson-Cook
Failure
Parameter
Average obtained fitted
values
1 D5 0.48105

19. Johnson-Cook Fracture model constants for Al 6061 alloy
𝐃 𝟏, 𝐃 𝟐 𝐃 𝟑 𝐃 𝟒 𝐃 𝟓
Constant D1 D2 D3 D4 D5
Al6061 0.51896 1.98319 6.80328 -0.07243 0.48105

20. Simulations
FEM Structure of Bullet and Al 6061 Square Plate
2mm above before impact

21. Simulations Results
FEM Analysis

22. Simulations Results
FEM Analysis

23. Simulations Results
FEM Analysis Results

24. School of Aeronautics
Major: Solid Mechanics
24