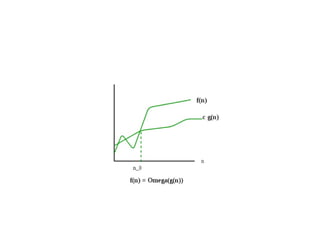
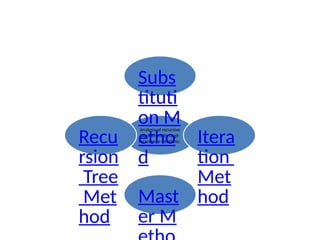
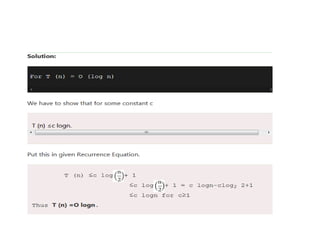
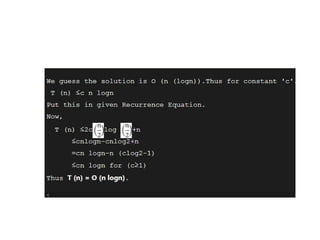
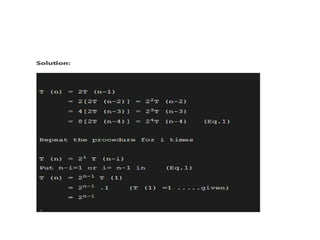
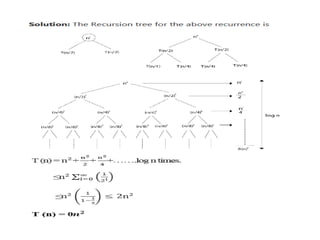
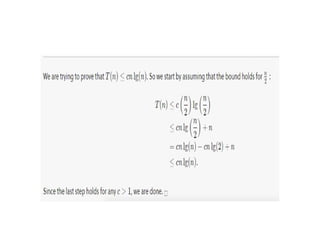The document provides an in-depth overview of algorithms, focusing on their characteristics, efficiency analysis through asymptotic notation, and performance comparisons. It discusses different types of performance measures, including time and space complexity, and methods for analyzing recursive algorithms, such as the substitution method, recursion tree method, and master theorem. Asymptotic analysis is emphasized as a crucial tool for evaluating algorithm efficiency by determining best, average, and worst-case scenarios.

2. • Module 1: Introduction
• Characteristics of algorithm.
• Analysis of algorithm: Asymptotic analysis of complexity
bounds – best, average and worst-case behavior;
• Performance measurements of Algorithm,
• Time and space trade-offs,
• Analysis of recursive algorithms through recurrence
relations: Substitution method, Recursion tree method
and Masters’ theorem.

3. Algorithm and Characteristics of algorithm:
• An algorithm is a finite set of instructions that, if followed, accomplishes a
particular task. In addition, all algorithms must satisfy the following criteria:
1. Input. Zero or more quantities are externally supplied.
2. Output. At least one quantity is produced.
3. Definiteness. Each instruction is clear and unambiguous. Unambiguous
means that the instructions given to an algorithm have simple one
interpretation, but not more than one interpretation.
4. Finiteness. If we trace out the instructions of an algorithm, then for all
cases, the algorithm terminates after a finite number of steps. This means
number of steps must be finite not infinite.
5. Effectiveness. Every instruction must be very basic so that it can be carried
out, in principle, by a person using only pencil and paper. It is not enough
that each operation be definite as in criterion3; it also must be feasible.

4. Analysis of algorithm: Asymptotic analysis of
complexity bounds – best, average and worst-
case behaviour

5. Asymptotic analysis:
• The efficiency of an algorithm depends on the amount
of time, storage and other resources required to
execute the algorithm. The efficiency is measured
with the help of asymptotic notations.
• An algorithm may not have the same performance for
different types of inputs. With the increase in the
input size, the performance will change.
• The study of change in performance of the algorithm
with the change in the order of the input size is
defined as asymptotic analysis.

6. • Asymptotic analysis of an algorithm refers to defining the mathematical
boundation/framing of its run-time performance. Using asymptotic analysis, we can very
well conclude the best case, average case, and worst case scenario of an algorithm.
• Asymptotic analysis is input bound i.e., if there's no input to the algorithm, it is concluded to
work in a constant time. Other than the "input" all other factors are considered constant.
• Asymptotic analysis refers to computing the running time of any operation in mathematical
units of computation. For example, the running time of one operation is computed as f(n) and
may be for another operation it is computed as g(n2
). This means the first operation running
time will increase linearly with the increase in n and the running time of the second operation
will increase exponentially when n increases. Similarly, the running time of both operations
will be nearly the same if n is significantly small.
• Usually, the time required by an algorithm falls under three types −
• Best Case − Minimum time required for program execution.
• Average Case − Average time required for program execution.
• Worst Case − Maximum time required for program execution.

7. Asymptotic Notations
• Asymptotic notations are the mathematical notations used to describe the
running time of an algorithm when the input tends towards a particular
value or a limiting value.
• For example: In bubble sort, when the input array is already sorted, the
time taken by the algorithm is linear i.e. the best case. But, when the input
array is in reverse condition, the algorithm takes the maximum time
(quadratic) to sort the elements i.e. the worst case.
• When the input array is neither sorted nor in reverse order, then it takes
average time. These durations are denoted using asymptotic notations.
• There are mainly three asymptotic notations:

8. Why is Asymptotic Notation Important?
• 1. They give simple characteristics of an
algorithm's efficiency.
• 2. They allow the comparisons of the
performances of various algorithms.

9. Performance analysis of an algorithm:
• Performance analysis of an algorithm is done
to understand how efficient that algorithm is
compared to another algorithm that solves
the same computational problem. Choosing
efficient algorithms means computer
programmers can write better and efficient
programs.

10. A computer resource is memory and CPU
time and performance analysis revolves around
these two resources. Two ways to evaluate an
algorithm is listed below.
• Space required to complete the task of that
algorithm (Space Complexity). It includes
program space and data space
• Time required to complete the task of that
algorithm (Time Complexity)

11. Space Complexity
• The space requirement is related to memory
resource needed by the algorithm to solve a
computational problem to completion. The
program source code has many types of
variables and their memory requirements are
different. So, you can divide the space
requirement into two parts.

12. • Fixed Variables
• The fixed part of the program are the instructions, simple variables, constants that does not
need much memory and they do not change during execution. They are free from the
characteristics of an instance of the computational problem.
• Dynamic Variables
• The variables depends on input size, pointers that refers to other variables dynamically, stack
space for recursion are some example. This type of memory requirement changes with instance
of the problem and depends on the instance characteristics. It is given by the following
equation.
• Instance characteristics means that it cannot be determined unless the instance of a problem
is running which is related to dynamic memory space. The input size usually has the control
over instance of a computational problem.

13. Time Complexity
• The time complexity is the amount of time
required to run the program to completion.It
is given by following.

15. • Big-O Notation (O-notation)
• Omega Notation (Ω-notation)
• Theta Notation (Θ-notation)

16. • 1. Theta Notation (Θ-Notation):
• Theta notation encloses the function from above and below. Since it
represents the upper and the lower bound of the running time of an
algorithm, it is used for analyzing the average-case complexity of an
algorithm.
• Let g and f be the function from the set of natural numbers to itself. The
function f is said to be Θ(g), if there are constants c1, c2 > 0 and a
natural number n0 such that c1* g(n) ≤ f(n) ≤ c2 * g(n) for all n ≥ n0
• Theta notation
• Mathematical Representation of Theta notation:
• Θ (g(n)) = {f(n): there exist positive constants c1, c2 and n0 such that 0 ≤
c1 * g(n) ≤ f(n) ≤ c2 * g(n) for all n ≥ n0}

17. 2. Big-O Notation (O-notation):
• Big-O notation represents the upper bound of the running time of an
algorithm. Therefore, it gives the worst-case complexity of an algorithm
or the longest amount of time an algorithm can possibly take to
complete..
• If f(n) describes the running time of an algorithm, f(n) is O(g(n)) if there
exist a positive constant C and n0 such that, 0 ≤ f(n) ≤ cg(n) for all n ≥ n0
• It returns the highest possible output value (big-O)for a given input.
• The execution time serves as an upper bound on the algorithm’s time
complexity.

18. 3. Omega Notation (Ω-Notation):
• Omega notation represents the lower bound of the running time
of an algorithm. Thus, it provides the best case complexity of an
algorithm or the best amount of time an algorithm can possibly
take to complete..
• The execution time serves as a both lower bound on the
algorithm’s time complexity.
• It is defined as the condition that allows an algorithm to
complete statement execution in the shortest amount of time.
• Let g and f be the function from the set of natural numbers to
itself. The function f is said to be Ω(g), if there is a constant c > 0
and a natural number n0 such that c*g(n) ≤ f(n) for all n ≥ n0
•

20. • Mathematical Representation of Omega
notation :
• Ω(g(n)) = { f(n): there exist positive constants c
and n0 such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }

21. Analysis of recursive algorithms through
recurrence relations: Substitution method,
Recursion tree method and Masters’
theorem.

22. Recurrence Relation
• A recurrence is an equation or inequality that
describes a function in terms of its values on
smaller inputs.
• To solve a Recurrence Relation means to
obtain a function defined on the natural
numbers that satisfy the recurrence.

23. Analysis of recursive
algorithms through
recurrence relations:
Subs
tituti
on M
etho
d
Itera
tion
Met
hod
Mast
er M
Recu
rsion
Tree
Met
hod

24. 1. Substitution Method:
The Substitution Method Consists of two main steps:
• Guess the Solution.
• Use the mathematical induction to find the boundary
condition and shows that the guess is correct.

25. For Example 1 Solve the equation by Substitution
Method.
We have to show that it is asymptotically bound by O
(log n).

29. • Example2 Consider the Recurrence
T (n) = 2T(n/2)+ n, n>1
Find an Asymptotic bound on T.

31. 2. Iteration Methods
• It means to expand the recurrence and express it as a summation of terms
of n and initial condition.

32. Example1: Consider the Recurrence

34. • Example2: Consider the Recurrence
• T (n) = T (n-1) +1 and T (1) = θ (1).

36. Recursion Tree Method
1. Recursion Tree Method is a pictorial representation of
an iteration method which is in the form of a tree
where at each level nodes are expanded.
2. In general, we consider the second term in recurrence
as root.
3. It is useful when the divide & Conquer algorithm is
used.
4. It is sometimes difficult to come up with a good guess.
In Recursion tree, each root and child represents the
cost of a single sub-problem.

37. 5. We sum the costs within each of the levels of
the tree to obtain a set of pre-level costs and
then sum all pre-level costs to determine the
total cost of all levels of the recursion.
6. A Recursion Tree is best used to generate a
good guess, which can be verified by the
Substitution Method.

38. Example 1

40. Master Method
• The Master Method is used for solving the following types of
recurrence

41. • n is the size of the problem.
• a is the number of sub-problems in the recursion.
• n/b is the size of each sub-problem. (Here it is assumed
that all sub-problems are essentially the same size.)
• f (n) is the sum of the work done outside the recursive
calls, which includes the sum of dividing the problem and
the sum of combining the solutions to the sub-problems.
• It is not possible always bound the function according to
the requirement, so we make three cases which will tell
us what kind of bound we can apply on the function.

42. • An asymptotically positive function means
that for a sufficiently large value of n, we
have f(n) > 0.

43. Master Theorem Cases-
• To solve recurrence relations using Master’s
theorem, we compare a with bk
.
Then, we follow the following cases-
• Case-01:

44. • Case-02:
Case-03:

45. • Problem-01:
• Solve the following recurrence relation using
Master’s theorem-
T(n) = 3T(n/2) + n2

46. Solution-
•
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nk
logp
n).
Then, we have-
a = 3
b = 2
k = 2
p = 0
•
Now, a = 3 and bk
= 22
= 4.
Clearly, a < bk
.
So, we follow case-03.
Since p = 0, so we have-
T(n) = θ (nk
logp
n)
T(n) = θ (n2
log0
n)
Thus,
T(n) = θ (n2
)

47. • Problem-02:
• Solve the following recurrence relation using
Master’s theorem-
T(n) = 2T(n/2) + nlogn

48. Solution-
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nk
logp
n).
Then, we have-
a = 2
b = 2
k = 1
p = 1
Now, a = 2 and bk = 21 = 2.
Clearly, a = bk
.
So, we follow case-02.
Since p = 1, so we have-
T(n) = θ (nlog
b
a
.logp+1
n)
T(n) = θ (nlog
2
2
.log1+1
n)
Thus,
T(n) = θ (nlog2
n)

49. Problem-03:
• Solve the following recurrence relation using
Master’s theorem-
T(n) = 2T(n/4) + n0.51

50. Solution-
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nk
logp
n).
Then, we have-
a = 2
b = 4
k = 0.51
p = 0
Now, a = 2 and bk = 40.51 = 2.0279.
Clearly, a < bk
.
So, we follow case-03.
Since p = 0, so we have-
T(n) = θ (nk
logp
n)
T(n) = θ (n0.51log0n)
Thus,
T(n) = θ (n0.51
)

51. Problem-04:
• Solve the following recurrence relation using
Master’s theorem-
T(n) = √2T(n/2) + logn

52. Solution-
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nklogpn).
Then, we have-
a = √2
b = 2
k = 0
p = 1
Now, a = √2 = 1.414 and bk
= 20
= 1.
Clearly, a > bk.
So, we follow case-01.
So, we have-
T(n) = θ (nlog
b
a
)
T(n) = θ (nlog
2
√2
)
T(n) = θ (n1/2
)
Thus,
T(n) = θ (√n)

53. Problem-05:
• Solve the following recurrence relation using
Master’s theorem-
T(n) = 8T(n/4) – n2
logn
• Solution-
The given recurrence relation does not correspond to
the general form of Master’s theorem.
So, it can not be solved using Master’s theorem.

54. Problem-06:
• Solve the following recurrence relation using
Master’s theorem-
• T(n) = 3T(n/3) + n/2
•

55. Solution-
We write the given recurrence relation as T(n) = 3T(n/3) + n.
This is because in the general form, we have θ for function f(n) which hides constants in it.
Now, we can easily apply Master’s theorem.
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nk
logp
n).
Then, we have-
a = 3
b = 3
k = 1
p = 0
Now, a = 3 and bk
= 31
= 3.
Clearly, a = bk
.
So, we follow case-02.
Since p = 0, so we have-
T(n) = θ (nlog
b
a
.logp+1
n)
T(n) = θ (nlog
3
3
.log0+1
n)
T(n) = θ (n1
.log1
n)
Thus,
T(n) = θ (nlogn)