More Related Content
PPTX
Edwards-Curve Digital Signature Algorithm (EdDSA) PPT
PPT
PPT
PPT
PDF
Why BFSI Company Should Partner With eTailing India? PDF
Introduction r-programming PDF
Viewers also liked
PDF
eTailing India Chennai Conclave 2013 Part 3 PDF
Tarun Arora- ATOM- eTailing India Conclave Jaipur- 2013 PPT
PPT
dene/Sunumlar/cab_abst.ppt DOCX
eCommerce Players Deliver Cash At Your Doorstep PPTX
PPTX
PDF
Web based inventory demand planning with sage connected services DOCX
Government Banks on Incentivising to Boost Digital Payment PDF
eTailing India Workshop - Retail Track- IBM Presentation PDF
eTailing India 3rd Annual Expo Event - Presentation by Ian Jindal (Internet r... DOCX
New channel distributions unlock retail india DOCX
महिलाएं भारतमे इकाँमर्सकी तरक्की कर रही है PDF
CCI Media Milan and Rome inventory PPTX
Atom Workshop : Payment Solutions For Modern Retail TXT
Examen 2° grado primer bimestre Similar to dene/ders2.ppt
PPT
PPTX
PDF
PPTX
Mat_Ders1_TaylorsssssssssssssSerisi.pptx PPT
Özel tanımlı fonksi̇yonlar 03 PDF
Sayisal yontemler 2 (1), nümerik analiz PDF
End331gecmissinavsorulari PPT
PPT
Fonksi̇yonlarin li̇mi̇ti̇ 01 PPTX
PPT
PPT
PPT
PPT
PPT
Fonksi̇yonlarin li̇mi̇ti̇ 02 PPT
REEL SAYILAR GERÇEK SAYILAR BİLİMSEL GÖSTERİM PPT
PPT
DOC
PPT
Fonksi̇yonlarin li̇mi̇ti̇ 03 More from Batın Düz
PDF
PDF
PPTX
dene/tiviace_english.pptx PPTX
dene/tiviace_english.pptx PDF
PPT
dene/TIVIACE_turkce03.ppt PPTX
PPT
PPT
PPT
PPT
PPT
PPT
PPT
PPT
PPT
dene/Sunumlar/cab_abst.ppt PPT
dene/Sunumlar/cab_abst.ppt PPT
dene/Sunumlar/cab_abst.ppt PPT
PPT
dene/ders2.ppt
- 1.
Algoritmalar
DERS 2
Asimptotik Notasyon
•O-, Ω-, ve Θ-notasyonları
Yinelemeler
•Yerine koyma metodu
•Yineleme döngüleri
•Özyineleme ağacı
•Ana Metot (Master metod)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.1
- 2.
Asimptotik notasyon
O-notasyonu(üst sınırlar):
Tüm n ≥ n0 değerleri için sabitler c > 0, n0 > 0 ise
0 ≤ f(n) ≤ cg(n) durumunda
f(n) = O(g(n)) yazabiliriz.
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.2
- 3.
Asimptotik notasyon
O-notasyonu(üst sınırlar):
Tüm n ≥ n0 değerleri için sabitler c > 0, n0 > 0 ise
0 ≤ f(n) ≤ cg(n) durumunda
f(n) = O(g(n)) yazabiliriz.
ÖRNEK: 2n2 = O(n3) (c = 1, n0 = 2)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.3
- 4.
Asimptotik notasyon
O-notasyonu(üst sınırlar):
Tüm n ≥ n0 değerleri için sabitler c > 0, n0 > 0 ise
0 ≤ f(n) ≤ cg(n) durumunda
f(n) = O(g(n)) yazabiliriz.
ÖRNEK: 2n2 = O(n3) (c = 1, n0 = 2)
fonksiyonlar,
değerler değil
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.4
- 5.
Asimptotik notasyon
O-notasyonu(üst sınırlar):
Tüm n ≥ n0 değerleri için sabitler c > 0, n0 > 0 ise
0 ≤ f(n) ≤ cg(n) durumunda
f(n) = O(g(n)) yazabiliriz.
ÖRNEK: 2n2 = O(n3) (c = 1, n0 = 2)
komik, “tek yönlü”
fonksiyonlar, eşitlik
değerler değil
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.5
- 6.
O-notasyonunun tanımı
O(g(n))= { f(n) : tüm n ≥ n0 değerlerinde
c > 0, n0 > 0 ise ve
0 ≤ f(n) ≤ cg(n) }
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.6
- 7.
O-notasyonunun tanımı
O(g(n))= { f(n) : tüm n ≥ n0 değerlerinde
c > 0, n0 > 0 ise ve
0 ≤ f(n) ≤ cg(n) }
ÖRNEK: 2n2 ∈ O(n3)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.7
- 8.
- 9.
Ω-notasyonu (alt sınırlar)
O-notasyonubir üst-sınır notasyonudur.
f(n) en az O(n2)'dir demenin bir anlamı yoktur.
Ω(g(n))= { f(n) : tüm n ≥ n0 değerlerinde
c > 0, n0 > 0 ise ve
0 ≤ cg(n) ≤ f(n) }
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.9
- 10.
Ω-notasyonu (alt sınırlar)
O-notasyonubir üst-sınır notasyonudur.
f(n) en az O(n2)'dir demenin bir anlamı yoktur.
Ω(g(n))= { f(n) : tüm n ≥ n0 değerlerinde
c > 0, n0 > 0 ise ve
0 ≤ cg(n) ≤ f(n) }
ÖRNEK: n = Ω (lg n) (c = 1, n0 = 16)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.10
- 11.
- 12.
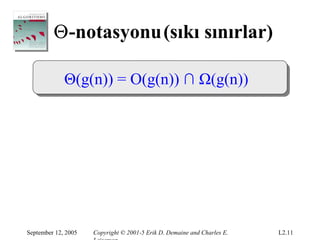
Θ-notasyonu(sıkı sınırlar)
Θ(g(n)) = O(g(n)) ∩ Ω(g(n))
ÖRNEK: 1
2
n2 − 2n = Θ(n2 )
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.12
- 13.
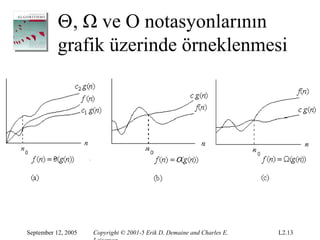
Θ, Ω veO notasyonlarının
grafik üzerinde örneklenmesi
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.13
- 14.
ο ve ωnotasyonları
O-notasyonu ve Ω-notasyonu ≤ ve ≥ gibidir.
o-notasyonu ve ω-notasyonu < ve > gibidir..
o(g(n))= { f(n) : tüm n ≥ n0 değerlerinde
c > 0 sabiti için n0 sabiti varsa
0 ≤ f(n) ≤ cg(n) }
ÖRNEK: 2n2 = o(n3) (n0 = 2/c)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.14
- 15.
ο ve ωnotasyonları
O-notasyonu ve Ω-notasyonu ≤ ve ≥ gibidir.
o-notasyonu ve ω-notasyonu < ve > gibidir..
o(g(n))= { f(n) : tüm n ≥ n0 değerlerinde
c > 0 sabiti için n0 sabiti varsa
0 ≤ f(n) ≤ cg(n) }
ÖRNEK: n = ω(lg n) (n0 = 1+1/c)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.15
- 16.
Yinelemelerin çözümü
• Ders 1' deki birleştirme sıralaması analizi bir
yinelemeyi çözmemizi gerektirmişti.
• Yinelemeler integral, türev, v.s.
denklemlerinin çözümlerine benzer.
• Ders 3: Yinelemelerin "böl-ve-fethet"
algoritmalarına uygulanması.
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.16
- 17.
Yerine koyma metodu(yöntemi)
En genel yöntem:
1.Çözümün şeklini tahmin edin.
2.Tümevarım ile doğrulayın.
3.Sabitleri çözün.
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.17
- 18.
Yerine koyma metodu(yöntemi)
En genel yöntem:
1.Çözümün şeklini tahmin edin.
2.Tümevarım ile doğrulayın.
3.Sabitleri çözün.
ÖRNEK: T(n) = 4T(n/2) + n
1. T(1) = Θ(1) olduğunu varsayın.
2. O(n3)'ü tahmin edin. (O ve Ω ayrı ayrı kanıtlayın.)
3. k< n için T(k) ≤ ck3 olduğunu varsayın.
• T(n) ≤ cn3'ü tümevarımla kanıtlayın.
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.18
- 19.
Yerine koyma örneği
T(n) = 4T (n / 2) + n
≤ 4c(n / 2)3 + n
= (c / 2)n3 + n
= cn3 − ((c / 2)n3 − n) istenen –kalan
≤ cn3 istenen
(c/2)n3 – n ≥ 0 olduğu zamanlarda, örneğin,
eğer c ≥ 2 ve n ≥ 1 ise.
kalan
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.19
- 20.
Örnek (devamı)
•Başlangıç koşullarını da ele almalı,yani,
tümevarımı taban şıklarına (base cases)
dayandırmalıyız.
•Taban: T(n) = Θ(1) tüm n < n0 için, ki n0
uygun bir sabittir.
•1 ≤ n < n0 için, elimizde “Θ(1)” ≤ cn3, olur;
yeterince büyük bir c değeri seçersek.
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.20
- 21.
Örnek (devamı)
•Başlangıç koşullarını da ele almalı,yani,
tümevarımı taban şıklarına (base cases)
dayandırmalıyız.
•Taban: T(n) = Θ(1) tüm n < n0 için, ki n0
uygun bir sabittir.
•1 ≤ n < n0 için, elimizde “Θ(1)” ≤ cn3, olur;
yeterince büyük bir c değeri seçersek.
Bu, sıkı bir sınır değildir !
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.21
- 22.
Daha sıkı birüst sınır?
T(n) = O(n2) olup olmadığını kanıtlayacağız.
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.22
- 23.
Daha sıkı birüst sınır?
T(n) = O(n2) olduğunu kanıtlayacağız.
Varsayın ki k < n için T(k) ≤ ck2 olsun:
T (n) = 4T (n / 2) + n
≤ 4c(n / 2)2 + n
= cn2 + n
= cn2 – (– n ) [ istenen –kalan ]
≤ cn2
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.23
- 24.
Daha sıkı birüst sınır?
T(n) = O(n2) olduğunu kanıtlayacağız. Varsayın
ki k < n için T(k) ≤ ck2 olsun:
T (n) = 4T (n / 2) + n
≤ 4c(n / 2)2 + n
= cn2 + n
= cn2 – (– n )
≤ cn2 Yanlış
c > 0 için eşitsizlik doğru değildir. Kaybettik.
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.24
- 25.
Özyineleme-ağacı metodu
• Özyineleme-ağacı,bir algoritmadaki özyineleme
uygulamasının maliyetini (zamanı) modeller.
• Özyineleme-ağacı metodu, bazen güvenilir
olmayabilir.
• Öte yandan özyineleme-ağacı metodu "öngörü"
olgusunu geliştirir.
• Özyineleme-ağacı metodu "yerine koyma
metodu" için gerekli tahminlemelerde yararlıdır .
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.25
- 26.
- 27.
Özyineleme-ağacı örneği
T(n) = T(n/4) + T(n/2) + n2: çözün
T(n)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.27
- 28.
Özyineleme-ağacı örneği
T(n) = T(n/4) + T(n/2) + n2: çözün
n2
T(n/4) T(n/2)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.28
- 29.
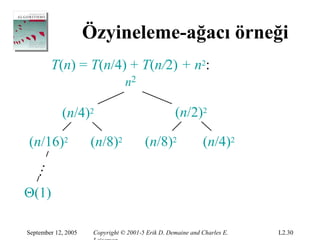
Özyineleme-ağacı örneği
T(n) = T(n/4) + T(n/2) + n2: çözün
n2
(n/4)2 (n/2)2
T(n/16) T(n/8) T(n/8) T(n/4)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.29
- 30.
Özyineleme-ağacı örneği
T(n) = T(n/4) + T(n/2) + n2:
n2
(n/4)2 (n/2)2
(n/16)2 (n/8)2 (n/8)2 (n/4)2
…
Θ(1)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.30
- 31.
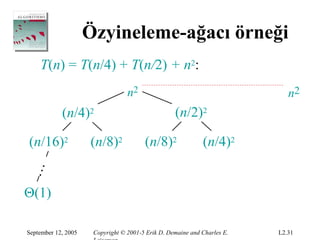
Özyineleme-ağacı örneği
T(n) = T(n/4) + T(n/2) + n2:
n2 n2
(n/4)2 (n/2)2
(n/16)2 (n/8)2 (n/8)2 (n/4)2
…
Θ(1)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.31
- 32.
Özyineleme-ağacı örneği
T(n) = T(n/4) + T(n/2) + n2:
n2 n2
(n/4)2 (n/2)2 5 n2
16
(n/16)2 (n/8)2 (n/8)2 (n/4)2
…
Θ(1)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.32
- 33.
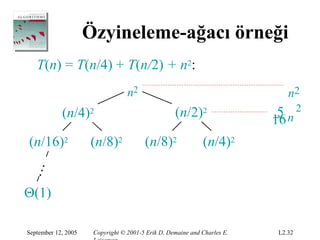
Özyineleme-ağacı örneği
T(n) = T(n/4) + T(n/2) + n2:
n2 n2
(n/4)2 (n/2)2 5 n2
16
(n/16)2 (n/8)2 (n/8)2 (n/4)2 25 n 2
256
…
Θ(1)
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.33
- 34.
Özyineleme-ağacı örneği
T(n) = T(n/4) + T(n/2) + n2:
n2 n2
(n/4)2 (n/2)2 5 n2
16
(n/16)2 (n/8)2 (n/8)2 (n/4)2 25 n 2
256
…
Θ(1) Toplam
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E.
- 35.
Ana Metod (TheMaster Method)
Ana method aşağıda belirtilen yapıdaki
yinelemelere uygulanır:
T(n) = a T(n/b) + f (n) ,
burada a ≥ 1, b > 1, ve f asimptotik olarak
pozitiftir.
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.35
- 36.
Üç yaygın uygulama
f(n)'i nlogba ile karşılaştırın:
1. f (n) = O(nlogba – ε) ε > 0 sabiti durumunda
• f (n) polinomsal olarak nlogba
göre daha yavaş büyür (nε faktörü oranında).
ÇÖZÜM: T(n) = Θ(nlogba) .
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.36
- 37.
Üç yaygın uygulama
f(n)'i nlogba ile karşılaştırın:
1.f (n) = O(nlogba – ε) ε > 0 sabiti durumunda;
• f (n) polinomsal olarak nlogba
göre daha yavaş büyür(nε faktörü oranında).
Çözüm: T(n) = Θ(nlogba) .
•f (n) = Θ(nlogba lgkn) k ≥ 0 sabiti durumunda;
• f (n) ve nlogba benzer oranlarda
Çözüm: T(n) =büyürler. k+1n) .
Θ(nlogba lg
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.37
- 38.
Üç yaygın uygulama
f(n)'i nlogba ile karşılaştırın:
3.f (n) = Ω(nlogba + ε)ε > 0 sabiti durumunda;
• f (n) polinomsal olarak nlogba 'ye göre daha
hızlı büyür ( nε faktörü oranında),
ve f (n), düzenlilik koşulunu af (n/b) ≤ cf (n)
durumunda, c < 1 olmak kaydıyla karşılar.
Çözüm: T(n) = Θ(f (n)) .
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.38
- 39.
Örnekler
Örnek. T(n) =4T(n/2) + n
a = 4, b = 2 ⇒ nlogba = n2; f (n) = n.
Durum 1: f (n) = O(n2 – ε) ε = 1 için.
∴ T(n) = Θ(n2).
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.39
- 40.
Örnekler
Ör. T(n) =4T(n/2) + n
a = 4, b = 2 ⇒ nlogba = n2; f (n) = n.
Durum 1: f (n) = O(n2 – ε) ε = 1 için.
∴ T(n) = Θ(n2).
Ör. T(n) = 4T(n/2) + n2
a = 4, b = 2 ⇒ nlogba = n2; f (n) = n2.
Durum 2: f (n) = Θ(n2lg0n), yani, k = 0.
∴ T(n) = Θ(n2lg n).
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.40
- 41.
Örnekler
Ör. T(n) =4T(n/2) + n3
a = 4, b = 2 ⇒ nlogba = n2; f (n) = n3.
DURUM 3: f (n) = Ω(n2 + ε) ε = 1için
ve 4(n/2)3 ≤ cn3 (düz. koş.) c = 1/2 için.
∴ T(n) = Θ(n3).
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.41
- 42.
Örnekler
Ör. T(n) =4T(n/2) + n3
a = 4, b = 2 ⇒ nlogba = n2; f (n) = n3.
DURUM 3: f (n) = Ω(n2 + ε) ε = 1için
ve 4(n/2)3 ≤ cn3 (düz. koş.) c = 1/2 için.
∴ T(n) = Θ(n3).
Ör. T(n) = 4T(n/2) + n2/lg n
a = 4, b = 2 ⇒ nlogba = n2; f (n) = n2/lg n.
Ana metod geçerli değil. Özellikle,
ε > 0 olan sabitler için nε = ω(lg n) elde edilir.
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.42
- 43.
Appendix/EK: Geometrik seriler
n+1
1−x ; x ≠ 1 için
1 + x + x + ... + x =2 n
1−x
1
1 + x + x + ... = 2 ; |x| < 1 için
1−x
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.43




















![Daha sıkı bir üst sınır?
T(n) = O(n2) olduğunu kanıtlayacağız.
Varsayın ki k < n için T(k) ≤ ck2 olsun:
T (n) = 4T (n / 2) + n
≤ 4c(n / 2)2 + n
= cn2 + n
= cn2 – (– n ) [ istenen –kalan ]
≤ cn2
September 12, 2005 Copyright © 2001-5 Erik D. Demaine and Charles E. L2.23](https://image.slidesharecdn.com/ders2-130220135737-phpapp02/85/dene-ders2-ppt-23-320.jpg)