Downloaded 44 times
Uploaded byJan Eite Bullema
2015 Deep learning and fuzzy logic
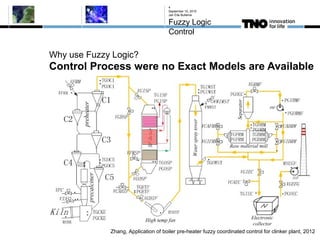
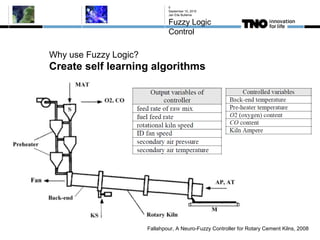
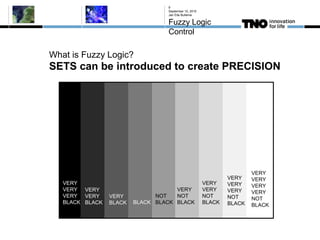
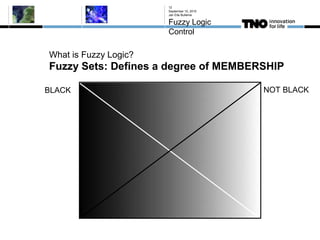
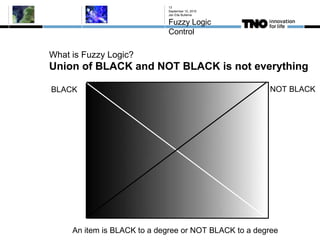
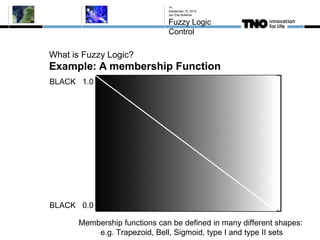
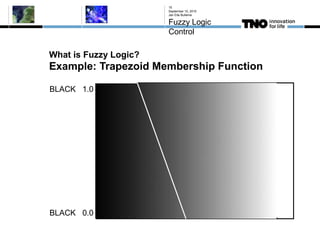
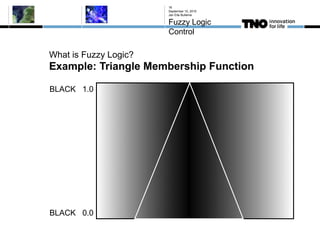
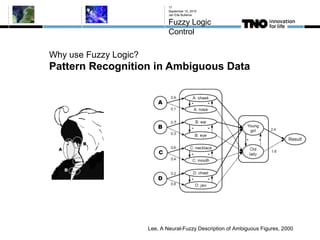
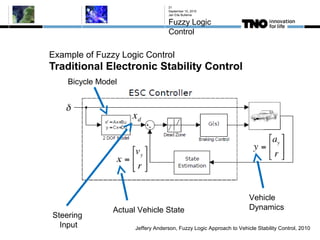
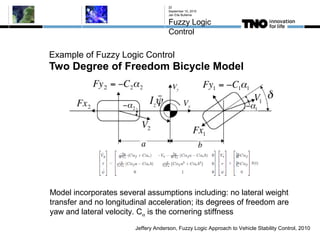
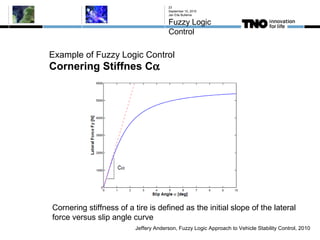
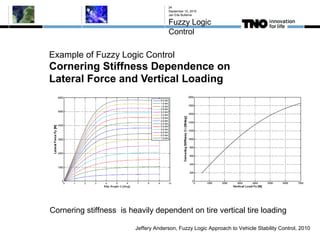
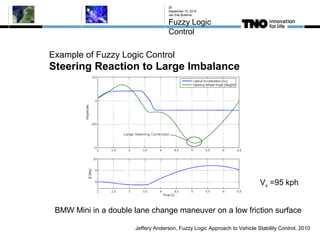
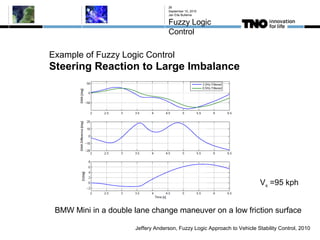
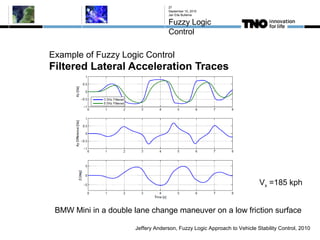
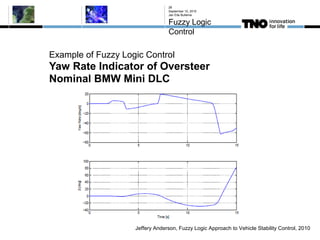
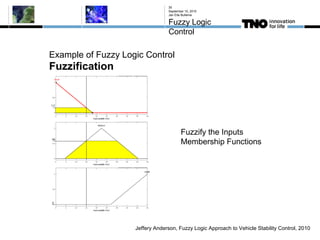
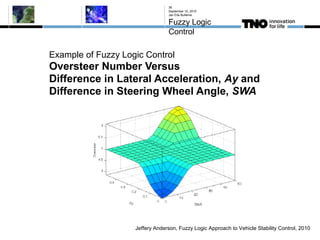
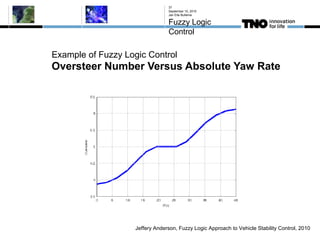
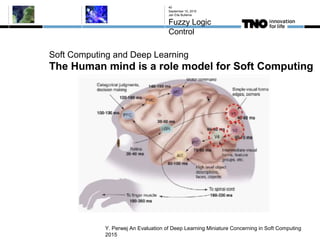
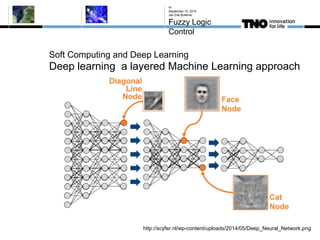
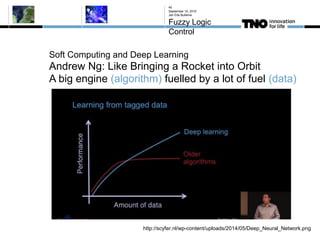
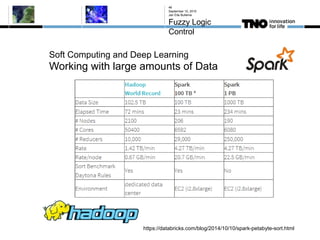
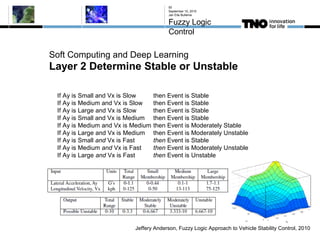
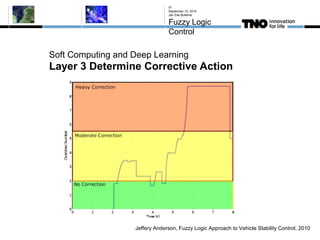
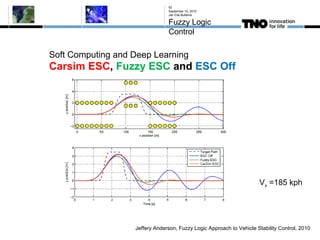
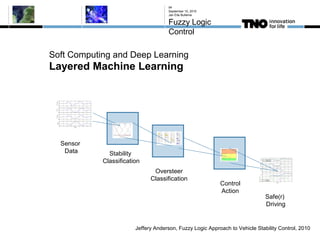
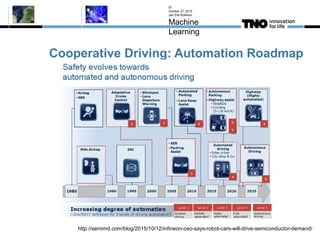
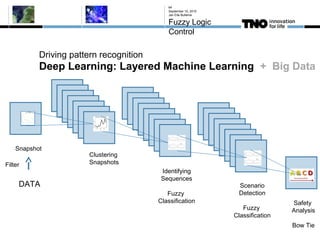
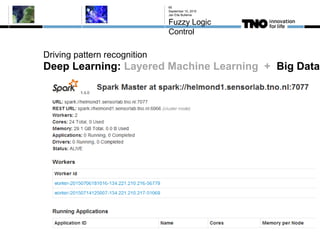
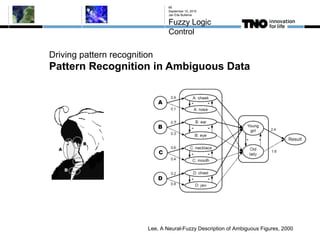
This document discusses fuzzy logic, its applications in areas such as machine learning and vehicle stability control, and its advantage in dealing with ambiguous or incomplete data. It provides examples of how fuzzy logic can enhance self-learning algorithms in soft computing and deep learning contexts. The document also touches on collaborative driving and the potential for reducing traffic accidents, congestion, and fuel consumption.
More Related Content
Similar to 2015 Deep learning and fuzzy logic
2015 Deep learning and fuzzy logic
- 1. Content: What is FuzzyLogic ? Why use Fuzzy Logic ? Example of Fuzzy Logic Soft Computing and Deep Learning Collaborative Driving Conclusion Machine Learning: "Field of study that gives computers the ability to learn without being explicitly programmed"
- 2. September 10, 2015 JanEite Bullema Fuzzy Logic Control 2 Content: What is Fuzzy Logic ? Why use Fuzzy Logic ? Example of Fuzzy Logic Soft Computing and Deep Learning Collaborative Driving Conclusion Machine Learning: "Field of study that gives computers the ability to learn without being explicitly programmed"
- 3. Why use FuzzyLogic? When Data is Ambiguous, Contradictory or Incomplete September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 3 Lee, A Neural-Fuzzy Description of Ambiguous Figures, 2000
- 4. Why use FuzzyLogic? Control Process were no Exact Models are Available September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 4 Zhang, Application of boiler pre-heater fuzzy coordinated control for clinker plant, 2012
- 5. Why use FuzzyLogic? Create self learning algorithms September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 5 Fallahpour, A Neuro-Fuzzy Controller for Rotary Cement Kilns, 2008
- 6. What is FuzzyLogic? The law of excluded middle September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 6 Shaved by the Barber Self Shavers Wolfram Lippe, Soft Computing, 2006, Springer ISBN-10 3-540-20972
- 7. What is FuzzyLogic? Classic Logic: item either is BLACK or NOT BLACK Union of BLACK and NOT BLACK is everything September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 7 NOT BLACKBLACK
- 8. What is FuzzyLogic? SET BOUNDARIES CAN BE A CHALLENGE September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 8 BLACK NOT BLACK
- 9. What is FuzzyLogic? SETS can be introduced to create PRECISION September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 9 VERY VERY VERY BLACK VERY VERY BLACK VERY BLACK BLACK VERY VERY VERY NOT BLACK VERY VERY NOT BLACK VERY NOT BLACK NOT BLACK VERY VERY VERY VERY NOT BLACK
- 10. What is FuzzyLogic? SETS can be introduced to create PRECISION September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 10 100% GREY100% BLACK 100% WHITE
- 11. What is FuzzyLogic? FUZZY LOGIC items can be partly ‘member’ of a SET September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 11 50% BLACK 50% NOT BLACK100% BLACK 100% NOT BLACK
- 12. What is FuzzyLogic? Fuzzy Sets: Defines a degree of MEMBERSHIP September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 12 BLACK NOT BLACK
- 13. What is FuzzyLogic? Union of BLACK and NOT BLACK is not everything September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 13 BLACK NOT BLACK An item is BLACK to a degree or NOT BLACK to a degree
- 14. What is FuzzyLogic? Example: A membership Function September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 14 BLACK 1.0 BLACK 0.0 Membership functions can be defined in many different shapes: e.g. Trapezoid, Bell, Sigmoid, type I and type II sets
- 15. What is FuzzyLogic? Example: Trapezoid Membership Function September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 15 BLACK 1.0 BLACK 0.0
- 16. What is FuzzyLogic? Example: Triangle Membership Function September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 16 BLACK 1.0 BLACK 0.0
- 17. Why use FuzzyLogic? Pattern Recognition in Ambiguous Data September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 17 Lee, A Neural-Fuzzy Description of Ambiguous Figures, 2000
- 18. September 10, 2015 JanEite Bullema Fuzzy Logic Control 18 Content: What is Fuzzy Logic ? Why use Fuzzy Logic ? Example of Fuzzy Logic Soft Computing and Deep Learning Collaborative Driving Conclusion Machine Learning: "Field of study that gives computers the ability to learn without being explicitly programmed"
- 19. Example of FuzzyLogic Control To Oversteer or not to Oversteer September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 19 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 20. Example of FuzzyLogic Control To Oversteer or not to Oversteer September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 20 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 21. Example of FuzzyLogic Control Traditional Electronic Stability Control September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 21 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 Steering Input Vehicle DynamicsActual Vehicle State Bicycle Model
- 22. Example of FuzzyLogic Control Two Degree of Freedom Bicycle Model September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 22 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 Model incorporates several assumptions including: no lateral weight transfer and no longitudinal acceleration; its degrees of freedom are yaw and lateral velocity. Cα is the cornering stiffness
- 23. Example of FuzzyLogic Control Cornering Stiffnes Cα September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 23 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 Cornering stiffness of a tire is defined as the initial slope of the lateral force versus slip angle curve
- 24. Example of FuzzyLogic Control Cornering Stiffness Dependence on Lateral Force and Vertical Loading September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 24 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 Cornering stiffness is heavily dependent on tire vertical tire loading
- 25. Example of FuzzyLogic Control Steering Reaction to Large Imbalance September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 25 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 BMW Mini in a double lane change maneuver on a low friction surface Vx =95 kph
- 26. Example of FuzzyLogic Control Steering Reaction to Large Imbalance September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 26 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 BMW Mini in a double lane change maneuver on a low friction surface Vx =95 kph
- 27. Example of FuzzyLogic Control Filtered Lateral Acceleration Traces September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 27 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 BMW Mini in a double lane change maneuver on a low friction surface Vx =185 kph
- 28. Example of FuzzyLogic Control Yaw Rate Indicator of Oversteer Nominal BMW Mini DLC September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 28 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 29. Example of FuzzyLogic Control Basic Steps in a Fuzzy Logic Algortihm September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 29 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 Fuzzify the Inputs Membership Functions Apply a Fuzzy Operator AND or OR Apply the Implication Operator THEN Aggregate the Output Evaluate Each Rule and Sum Results Defuzzify the Aggregate Return Degree of Output from the Inputs
- 30. Example of FuzzyLogic Control Fuzzification September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 30 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 Fuzzify the Inputs Membership Functions
- 31. Example of FuzzyLogic Control Apply a Fuzzy Operator September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 31 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 If SWA is Small and Ay is Small then Oversteer is No Oversteer
- 32. Example of FuzzyLogic Control Apply the Implication Operator September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 32 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 Yaw Rate (AVz) Membership Evaluated for Moderate Oversteer, deg/s. If AVz is Medium then Oversteer is Moderate Oversteer
- 33. Example of FuzzyLogic Control Defuzzify the Aggregate September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 33 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 34. Example of FuzzyLogic Control For the September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 34 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 35. Example of FuzzyLogic Control Fuzzy Logic Process September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 35 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 If SWA is Small and Ay is Small then Oversteer is No Oversteer If SWA is Medium and Ay is Medium then Oversteer is Moderate Oversteer If SWA is Large and Ay is Large then Oversteer is Heavy Oversteer If AVz (i.e., yaw rate) is Small then Oversteer is No Oversteer If AVz is Medium then Oversteer is Moderate Oversteer If AVz is Large then Oversteer is Heavy Oversteer
- 36. Example of FuzzyLogic Control Oversteer Number Versus Difference in Lateral Acceleration, Ay and Difference in Steering Wheel Angle, SWA September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 36 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 37. Example of FuzzyLogic Control Oversteer Number Versus Absolute Yaw Rate September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 37 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 38. September 10, 2015 JanEite Bullema Fuzzy Logic Control 38 Content: What is Fuzzy Logic ? Why use Fuzzy Logic ? Example of Fuzzy Logic Soft Computing and Deep Learning Collaborative Driving Conclusion Machine Learning: "Field of study that gives computers the ability to learn without being explicitly programmed"
- 39. Soft Computing andDeep Learning Soft computing differs from conventional (hard) computing in that, unlike hard computing, it is tolerant of imprecision, uncertainty, partial truth, and approximation September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 39 http://www.soft-computing.de/def.html Fuzzy Systems Neural Networks Evolutionary Computing Machine Learning Probabilistic Reasoning Bayesian Networks Support Vector Machines (Restricted) Boltzmann Machines
- 40. Soft Computing andDeep Learning The Human mind is a role model for Soft Computing September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 40 Y. Perwej An Evaluation of Deep Learning Miniature Concerning in Soft Computing 2015
- 41. Soft Computing andDeep Learning Deep learning a layered Machine Learning approach September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 41 http://scyfer.nl/wp-content/uploads/2014/05/Deep_Neural_Network.png
- 42. Soft Computing andDeep Learning Neural Network for Pattern Recognition September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 42 Hinton, A fast learning algorithm for deep belief nets, Neural Computation, 2006
- 43. Soft Computing andDeep Learning Neural Network for Pattern Recognition September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 43 Hinton, Coursera course: Neural Networks for Machine Learning, 2012 Hinton, A fast learning algorithm for deep belief nets, Neural Computation, 2006
- 44. Soft Computing andDeep Learning Neural Network for Pattern Generation September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 44 Hinton, Coursera course: Neural Networks for Machine Learning, 2012 Hinton, A fast learning algorithm for deep belief nets, Neural Computation, 2006
- 45. Soft Computing andDeep Learning Andrew Ng: Like Bringing a Rocket into Orbit A big engine (algorithm) fuelled by a lot of fuel (data) September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 45 http://scyfer.nl/wp-content/uploads/2014/05/Deep_Neural_Network.png
- 46. Soft Computing andDeep Learning Working with large amounts of Data September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 46 https://databricks.com/blog/2014/10/10/spark-petabyte-sort.html
- 47. Soft Computing andDeep Learning To Oversteer or not to Oversteer September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 47 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 48. Soft Computing andDeep Learning Stable or Unstable September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 48 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 If SWA is Small and Ay is Small then Oversteer is No Oversteer If SWA is Medium and Ay is Medium then Oversteer is Moderate Oversteer If SWA is Large and Ay is Large then Oversteer is Heavy Oversteer If AVz is Small then Oversteer is No Oversteer If AVz is Medium then Oversteer is Moderate Oversteer If AVz is Large then Oversteer is Heavy Oversteer At low speeds the driver will tend to steer much more than at high speed; this can lead to a false indication of oversteer e.g. at parking lot speeds
- 49. Soft Computing andDeep Learning Layer 1 Determine Oversteer September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 49 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 50. Soft Computing andDeep Learning Layer 2 Determine Stable or Unstable September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 50 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 If Ay is Small and Vx is Slow then Event is Stable If Ay is Medium and Vx is Slow then Event is Stable If Ay is Large and Vx is Slow then Event is Stable If Ay is Small and Vx is Medium then Event is Stable If Ay is Medium and Vx is Medium then Event is Moderately Stable If Ay is Large and Vx is Medium then Event is Moderately Unstable If Ay is Small and Vx is Fast then Event is Stable If Ay is Medium and Vx is Fast then Event is Moderately Unstable If Ay is Large and Vx is Fast then Event is Unstable
- 51. Soft Computing andDeep Learning Layer 3 Determine Corrective Action September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 51 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010
- 52. Soft Computing andDeep Learning Carsim ESC, Fuzzy ESC and ESC Off September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 52 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 Vx =185 kph
- 53. Soft Computing andDeep Learning Layered Machine Learning September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 54 Jeffery Anderson, Fuzzy Logic Approach to Vehicle Stability Control, 2010 Oversteer Classification Stability Classification Control Action Safe(r) Driving Sensor Data
- 54. September 10, 2015 JanEite Bullema Fuzzy Logic Control 55 Content: What is Fuzzy Logic ? Why use Fuzzy Logic ? Example of Fuzzy Logic Soft Computing and Deep Learning Collaborative Driving Conclusion Machine Learning: "Field of study that gives computers the ability to learn without being explicitly programmed"
- 55. Cooperative Driving: SomeFigures October 27, 2015 Jan Eite Bullema Machine Learning 56 -Traffic fatalities (1.3 million deaths/year across the globe) can be reduced, as 90% of all accidents are caused by human errors -Less traffic congestion: Today, US commuter spend 38 hours/year in traffic jams, which are causing total costs of $121 billion/year -Improved fuel efficiency (up to 50%) http://semimd.com/blog/2015/10/12/infineon-ceo-says-robot-cars-will-drive-semiconductor-demand/
- 56. Cooperative Driving: AutomationRoadmap October 27, 2015 Jan Eite Bullema Machine Learning 57 http://semimd.com/blog/2015/10/12/infineon-ceo-says-robot-cars-will-drive-semiconductor-demand/
- 57. Driving pattern recognition TypicalTest Drive in the Helmond area September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 58 https://city.tno.nl/Koning maakt kennis met automatisch rijden
- 58. Driving pattern recognition SupervisedNeural Network Classification September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 59 J.E. Bullema, TNO Colloquium Fuzzy Logic Control, 2015
- 59. Use of BigData: Deep Learning Approach September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 60 Driving pattern recognition: Lane Change Feature Mapping: Car Driving on an Oval and Cutting in a Platoon CONFIDENTIAL DATA IS NOT SHOWN HERE
- 60. Use of BigData: Deep Learning Approach September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 61 Driving pattern recognition: Lane Change Feature Mapping: Fast Lane Change / Cut In Fast Lane Change CONFIDENTIAL DATA IS NOT SHOWN HERE
- 61. Use of BigData: Deep Learning Approach September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 62 Driving pattern recognition: Lane Change Feature Mapping: Medium Lane Change / Cut In Normal Lane Change CONFIDENTIAL DATA IS NOT SHOWN HERE
- 62. Use of BigData: Deep Learning Approach September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 63 Lelystad Platoon Driving Data Set 24-03-2015 Driving pattern recognition: Lane Change Feature Mapping: Slow Lane Change / Cut in Slow Lane Change ? CONFIDENTIAL DATA IS NOT SHOWN HERE
- 63. Driving pattern recognition DeepLearning: Layered Machine Learning + Big Data September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 64 Snapshot Clustering Snapshots Identifying Sequences Fuzzy Classification Scenario Detection Fuzzy Classification Filter Safety Analysis Bow Tie DATA
- 64. Driving pattern recognition DeepLearning: Layered Machine Learning + Big Data September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 65
- 65. Driving pattern recognition PatternRecognition in Ambiguous Data September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 66 Lee, A Neural-Fuzzy Description of Ambiguous Figures, 2000
- 66. CONCLUSION Layered Machine Learningbased upon Fuzzy Logic September 10, 2015 Jan Eite Bullema Fuzzy Logic Control 67 Work with Expert input without need for exact models Work with imprecise data Easier to develop layered topologies using Fuzzy Logic Better understanding what it does Possible to create neural networks Generate new scenarios with the neural network Use Big Data technologies (Spark)
Editor's Notes
- #2 This painting is a painting by Matisse. It is a painting called: “The fall of Icarus” I use this painting for this colloquium lecture, because twenty years ago, there was a German company called Fuzzytech that had this Matisse painting as their poster. Also whit the text precision is not thruth. I have had this poster of Fuzzytech for more than ten years over my desk at home. Because I liked this basic concept of Fuzzy Logic very much: Precision is not truth. Twenty years ago I gave a Fuzzy Logic course for CTT and Fontys, because I had made several Fuzzy Control algorithms and had become a national expert in Fuzzy Logic. Eventually the Fuzzy Logic hype dwindled down and I proceeded concentrating on other advanced process control methods A few months ago I encounter in the Crystal project a classification problem, for safety evaluation of autonomous driving, that could be solved using Fuzzy Logic. So I read about the latest developments and saw that there have been interesting developments in this field. New set theory and potential coupling of Fuzzy Logic with Big Data analytics. I decided to give this colloquium, based upon my old three day Fuzzy Logic course. So I start with a concise introduction, give an example of an application. And then jump into the developments in soft computing and deep learning, which is a broader than fuzzy logic. The precision is not truth part of the lecture is an outline of my current work for safety classification of collaborative driving.
- #3 So what is Fuzzy Logic. Fuzzy Logic, probably the better name for fuzzy logic would have been, multi value logic. As ‘fuzzy’ has an unscientific sound to it. Later the term soft computing was introduced to refer to a group of similar methods: Fuzzy Logic, Neural Networks and Genetic Algorithms. I will not go into all details of fuzzy logic but show two elements of fuzzy logic: the fuzzy set theory and how fuzzy logic differs from classic logic Fuzzy Logic makes it possible to use imprecise measurements, imprecise reasoning to create control models. There are famous control scientists who hate this aspect of imprecise reasoning. Imprecise reasoning leads in their opinion to unscientific conclusions. For instance Rudolf Kalman made the following comment: Fuzzification ' is a kind of scientific permissiveness. It tends to result in socially appealing slogans unaccompanied by the discipline of hard scientific work and patient observation.
- #4 Why use fuzzy logic. One reason is that fuzzy logic makes it possible to work with ambiguous, contradictory or uncomplete information. I start with this famous optical illusion were one can see a young girl and an old woman, or "wife" and "mother in law". So we can see both in the same picture. It is an old lady and it is a young lady. I will show later on that we can use fuzzy logic to analyze the picture and classify the picture. Fuzzy Lofic is actually used for –image- classification problems in
- #5 One of the first well known industrial examples of application of fuzzy control – already in the mid-ninetees, is fuzzy control for firing a rotary cement kiln. Operators can control the cement kiln process based upon their experience. If the cement is slighlty wet then Increase the fan speed a little. This kind of linguistic , experience based process model can be captured using fuzzy logic. Due to complexity and non linearity it is difficult (expensive or impossible) to control the process with exact models.
- #6 Besides using human experience and insights it is also possible to create self learning algorithms. Every Fuzzy Logic algorithm can be written as a neural network. And obne can use the self learning ability of neural networks. ===== Patent US 4910684 A Method of controlling a rotary kiln during start-up To facilitate a smooth and quick start-up of a rotary kiln, a Fuzzy Logic Control system is proposed, the principal feature of which is to mandate control actions to decrease the specific heat consumption along a straight line from an initial high value to a steady-state value established for the kiln, and then to switch over to an existing steady-state fuzzy logic control mode. In the start-up phase, further process variables are preferably measured and monitored against reference values to mandate concurrent control actions influencing the Fuzzy Logic Control system in a weighted manner.
- #7 I can not give my entire course in fuzzy logic in an hour so I pick out one element of fuzzy logic. The fuzzy sets. Proposed by Lofti Zadeh in the mid sixties. In classical logic an expression either must be true or must be false. Classic logic finds ist origin in the greek philiosopher Aristotel, who formulated the law of the excluded middle In logic, the law of excluded middle (or the principle of excluded middle) is the third of the three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is true. About 100 years ago the British Filosofer an later Nobel Price (1950) laureate Berrtrand Russels made the comment that “The law of excluded middle is true when precise symbols are employed, but it is not true when symbols are vague, as, in fact, all symbols are.” Russel illustrated this by the example of the barber’s paradox: in a small Spanish village men either shave them selves or they are shaven by the barber. So the question is: in which group is the barber? The classic law of the excluded middle is insufficient in case of this paradox.
- #8 In classic logic an item is black or not black. The union of black and not-black is the entire universe.
- #9 In reality, we often have to deal with less sharp boundaries.
- #10 We could try to introduce extra sets to have more precise descriptions (note that this also leads to an explosion of rules when we want to describe relationships between sets)
- #11 Or we could try to use different descriptions, in stead of calling everything black or not black introduce other views on the world. Which also complicates model description and we still have a problem of definition. I am not happy with the 100% White and the 100% Black.
- #12 We also could say there is an additional region which is half not black and half black. So this also would require additional sets I think.
- #13 The solution proposed by Lofti Zadeh in 1965 is the introduction of Fuzzy Sets, were an item is partly member of a set. And degree of membership is described by a membership function. This looks simple, but is a big thing, which can be made very useful as I will demonstrate in the colloquium.
- #14 In fuzzy logic one use is the concept that an item is Black to a degree and not-black to a degree. The degree could be 100%. And then we have the case of classic logic again. So Fuzzy Logic includes classic logic as a special case were all items are full member of a set or no member. Another interesting aspect is that in this fuzzy approach the union of fuzzy sets is no longer the entire universe. This creates room for paradox or incompleteness. You do not have to procrastinate, you can start with incomplete knowledge and learn more later.
- #15 The membership function can be used to describe the level in which an element or an observation is part (member) of a specific set. So we do not have to describe the world in many, many different set but can work with some main categories. Often Low Medium and High and permutations like: Very Low, Very Very Low, Very Very Very Low. For most control application u of three (L, M, H) to five sets (VL, L , M, H, VH) are a good starting point. The shape of a membership function can take any form which suits best the needs for an accurate description. For instance if you have statistical information, you could use Gaussian shapes derived from mean and standard deviation.
- #16 Much used shapes for membership functions of fuzzy sets are trapezoid shape and the triangular shape.
- #17 Much used shapes for membership functions of fuzzy sets are trapezoid shape and the triangular shape. The membership function can be used to describe the level in which an element or an observation is part (member) of a specific set. So we do not have to describe the world in many, many different set but can work with some main categories. In real life we nearly never work with precise data ,when you drive a car you seldom estimate: the car in front of me is far away. Not the car in front of me is 105,34 m in front of me.
- #18 I started with the optical illusion were one can see a young girl and an old woman, or "wife" and "mother in law". I show this to give an example. The real pattern recognition poses a lot of additional challenges. One could use fuzzy sets to decide what is in the picture. So looking at specific elements in the picture. For instance to what degree is the segment B and Eye and to what degree is the segment B an Ear. In the example the algorithm gives a degree of membership of 0.7 for the ear and a degree of membership of 0.3 for the eye. Looking at different sections (in this case the regions A, B, C, D) the cumulated degrees of membership for young girl are 2.4 and the cumulated degrees of membership for the old lady are 1.6. So this algorithm would return a crisp classification: the picture is young girl What an algorithm gives as classification depends on the purpose: ‘What do you want to see’ or what kind of supervised data have you presented to train the algorithm.
- #19 It is not possible to give a complete introduction into fuzzy logic, but I have demonstrated the fuzzy set and pointed towards the use of fuzzy logic to describe difficult to model processes, work with ambiguous or incomplete data, use fuzzy logic in adaptive learning controllers. I mentioned the operational robustness of fuzzy controllers. Position of sets number of sets missing rules all do little with general performance So we now go to an example. The example is related to the automotive case of Crystal.
- #20 Technically speaking, oversteer means that a car's rear tires are operating at a greater slip angle than the front tires, i.e., they're working harder. In real-world terms, it means the tail of the car is sliding sideways. Holding the car in this dynamic state results in a glorious drift. Failing to hold it usually ends with an inglorious spin. Controlling oversteer in a rear-drive car is all about separately regulating the lateral velocity at each end of the vehicle. In the example I will not go into all details, I just go through the steps which are used in developing a fuzzy controller.
- #21 Technically speaking, oversteer means that a car's rear tires are operating at a greater slip angle than the front tires. Professional rally drivers can use oversteer to go as fast as possible a turn. By handling the car. Normal drivers mostly end in a spin and in the shrubs. Or subsequently a collision can take place. Electronic Stability Control can be used to prevent a car to come into an oversteer situation. So how does an ESC algorithm works and can we apply fuzzy logic. ====== Electronic Stability Control is a very heavily researched topic with widely understood benefits to the safety of transportation. The Department of Transportation estimates thirty-four percent of single-vehicle passenger car crashes and fifty-nine percent of single-vehicle Sport Utility Vehicles (SUVs) crashes could be prevented with the implementation stability control; moreover, it will be federally mandated that in the model year 2012, all light vehicles will be required to have ESC. These estimations suggest the dramatic potential to save lives which is why this topic is of such importance
- #22 Let us first look at the traditional approach for Electronic Stability Control. The traditional ECC strategy depends on the use of linear observers as seen in the diagram. This strategy commonly uses the two degree of freedom bicycle model as the observer to estimate the vehicle states based on the steering input to the model (xd). It is a closed loop observer that uses measured vehicle dynamics (y) and a state estimator to turn those sensor traces into estimates of the actual vehicle state (x) and is compared to the estimated traces from the vehicle model. A controller acts on these states and commands differential braking tot the appropriate wheel to prevent te vehicle from spinning out
- #23 The two degree of freedom model is the essential problem in this approach; it heavily depends on several assumptions and accurate vehicle parameters to work correctly. F igure represents the vehicle model as the two front tires and two rear tires combined. This model incorperates several assumptions including: no lateral weight transfer and no longitudinal acceleration; thus, its degrees of freedom are yaw and lateral velocity. Forces and moments can be summed about the center of gravity and put in state space form as seen in Equation 1.1 . Note that the C terms are the front and rear cornering stiffnesses as seen in Figure C is the initial slope of the lateral force versus slip angle curve.
- #24 As seen in Figure, the cornering stiffness of a tire is defined as the initial slope of the lateral force versus slip angle curve. This means that the vehicle model is only valid where C accurately describes the lateral force capability of the tire or the linear regime of the tire which is only valid to approximately 0.3 G. Cornering stiffness is also heavily dependent on tire vertical tire loading which is illustrated with the tire data in Figure 1.4.
- #25 Cornering stiffness is also heavily dependent on tire vertical tire loading which is illustrated with the tire data in the figures. Higher load higher cornering stiffness, less oversteer problems. In the two degree of freedom model, the coefficient of friction between the tire and the road is assumed such that that the tires do not saturate. This is especially problematic in low mu (low friction surfaces, like an icy road) situations where the tires easily saturate and induce instability. A more robust algorithm is needed, can we do that with fuzzy logic?
- #26 First we have to build a model. We can use experiences of drivers. Steering can give a good indicator of a driver’s reaction to an imbalance in the vehicle. In the case of oversteer the driver will tend to reduce the steering wheel angle to prevent the vehicle from spinning-out. This can be seen in Figure, where the test care, a nominal BMW Mini in a double lane change (DLC) maneuver on a low friction surface is plotted. (Mu =0,2) . Speed is 95 km/hr. We see steering wheel angle (normalized) and lateral acceleration. And sideslip (drifthoek in NL) We see here: As the driver made the second turn (3.5 s), the tires saturated which produced a plateau effect on lateral acceleration. Moreover, the driver starts to counter-steer (5.0 s) to prevent the vehicle from spinning. At the same time, the vehicle sideslip angle is over 5 deg which is quite large and indicates that the driver barely maintained control of the vehicle. This illustrates how the driver’s reaction can be analyzed to determine an oversteer situation.
- #27 The raw data will be initially low-pass filtered at 3.5 Hz. This is the approximate bandwidth of an average driver and this removes high frequency content from other sources such as vehicle interference (i.e, noise and vibrations). It should be noted since this is a real-time algorithm, a first order filter is used to prevent as much lag as possible in the data conditioning step. The data is low-pass filtered again at 0.5 Hz. The remaining low frequency content represents the activity of a ”balanced” driver. It eliminates much of the driver’s corrections to the imbalances and preserves the general steering inputs. The difference between these two filtered sets represents the driver’s reaction to the imbalances in the vehicle. For the same example as before (the low surface , Mini DLC), the filtered signal traces for steering wheel angle are seen in Figure . A large correction is indicated at 3.5 s and 5 s. Both indicate the driver’s reaction to imbalance. However, considering the vehicle sideslip trace, it is evident that the 5 s indicator is much more important than the 3.5 s indicator because of the magnitude of the vehicle sideslip angle. From this example, it is clear that steering wheel angle can be used to indicate oversteer; however, it must be considered together with the other indicating signals.
- #28 The two filtered acceleration signals, the difference in these acceleration signals, and the vehicle side slip angle are plotted. At 4.7 and 7 s there are concurrent spikes in both the lateral acceleration difference and the vehicle sideslip that suggest oversteer. However, at 2 s, the spike in lateral acceleration difference does not correspond to a large sideslip angle. Therefore, lateral acceleration alone cannot indicate oversteer.
- #29 So we can use the lateral acceleration and the difference in steering wheel angle for analyses of oversteer. The final signal that is used in this ESC algorithm is yaw rate. This signal is a physical check for the rest of the system. If yaw rate is too large, the vehicle is spinning-out. The previous indicator involving steering wheel angle and lateral acceleration depends on the driver’s reaction to the imbalance. It is clear in Figure that after 12 s of the run, the vehicle is spinning-out because of the excessively high yaw rate ( Yaw rate > 60 deg/s) and extremely high sideslip ( Beta> 20 deg). This signal combined with the steering difference and lateral acceleration difference will be the three signals examined in the fuzzy logic to determine a level of oversteer present in the vehicle at each instant.
- #30 These are the basic steps, fuzzification, apply a fuzzy operator, apply a fuzzy implication operator, aggregate the output and the defuzzify the aggregate. It is all quit simple, I will show it in a few graphs. I will not go in to details of how one comes to these rules and how to generate the specific sets. We have three input parameters difference in Steering Wheel Angle and Lateral Acceleration and Yaw rate.
- #31 Fuzzification, each input needs to be placed in a fuzzy domain which deals with linguistic operators. For example, Figure shows yaw rate has three membership functions to determine the level of yaw rate: low, medium, and high. The shape and position and number of sets can come from experiments or insights. Typically a fuzzy logic tool (in R, Python, Matlab, done it in excel) box takes the current level of yaw rate (AVz) and evaluates how it fits into each membership function. For instance, if the current level of yaw rate is 15 deg/s, the fuzzy logic would evaluate the low yaw rate membership as 0.2, the moderate yaw rate as 0.55, and the high yaw rate as 0 as illustrated in Figure The property of the Fuzzy Set Yaw Rate is Low and Medium at the same time but at different degrees.
- #32 After each input has been fuzzified, the fuzzy operator can be applied. In this case a simple AND or OR operator that is used when dealing with multi-input rules. For example, When the difference in steering is large AND the difference in lateral acceleration is large, then, the level of oversteer is high.
- #33 Implication is done by applying the consequence to the degree of membership. So we have a rule that says if Yaw Rate is Medium then Oversteer is Medium. If Yaw Rate Medium is 0.55 as in the exampel, we cut of the Medium Oversteer at 0.55.
- #34 Aggregate the Output for Each Rule Defuzzify the Aggregate. Finally, a single aggregated output exists that covers the entire space of the output variable. In this step, a single number will be returned from this aggregated output. In the graph all basic steps of a fuzzy algorithm are shown.
- #35 In an algorithm all rules are evaluated simultaneously to come to a crisp result. So the algorithm does not lead to a vague result, but to a crisp single value outcome. Based upon crisp sensor input signals there is a crisp output. Given the SWA input of 2.18 he Lateral Acceleration of 0.133 and the Yaw Rate of 8.3. The output of the algorithm for Oversteer is 3.32. We will late see what we can do whit this.
- #36 The following is the set of rules used to determine the level of oversteer present, and are summarized in the next Figure where the input parameters are mapped to a level of output. As said you can use Design of Experiment, Insights, Experience, Theory to derive these rules and derive the location and shape of the membership functions. In fact most fuzzy controlers are quite robust for choices if five sets gigve a good performance then seven sets or three sets give most likely also good performance. Classification of Oversteer is done in a scale from 1 tot 10 later we will use this classification.
- #37 Since lateral acceleration and steering wheel angle are combined in each rule, they are plotted together in this so-called response graph to show their contribution to the oversteer number.
- #38 Yaw rate is independent of the other two variables and is plotted alone to show its contribution to the output. So we now have a feeling for how a fuzzy logic controller works and we have a feeling of the way knowledge is represented in a fuzzy controller. Later we will see some driving tests with the algorithm.
- #39 So we can classify oversteer, now we I want to go into the current hype of deep learning. Deep learning is a hot thing since a few years. The Deep Learning hype started, I think with, the 2012 google project to recognize cats in youtube videos. The “brain” simulation was exposed to 10 million randomly selected YouTube video thumbnails over the course of three days and, after being presented with a list of 20,000 different items, it began to recognize pictures of cats using a “deep learning” algorithm. This was despite being fed no information on distinguishing features that might help identify one.
- #40 First something about soft computing. Soft computing differs from conventional (hard) computing in that, unlike hard computing, it is tolerant of imprecision, uncertainty, partial truth, and approximation. In effect, the role model for soft computing is the human mind. According to Lofti Zadeh, the principal constituents of soft computing (SC) are fuzzy logic (FL), neural network theory (NN) and probabilistic reasoning (PR), with the latter subsuming belief networks, evolutionary computing including DNA computing, chaos theory and parts of learning theory. Soft computing differs from conventional (hard) computing in that, unlike hard computing, it is tolerant of imprecision, uncertainty, partial truth, and approximation.
- #41 In recent years, Deep Learning at the latest developed field belonging to soft computing. The Deep learning has been a hot topic in the communities of artificial intelligence, artificial neural networks and machine learning. The deep learning paradigm tackles problems in which shallow architectures are impressed with the curse of dimensionality. Deep architectures are composed of multiple levels of non-linear operations, such as in neural nets with many hidden layers or in complicated propositional formulae re-using many sub-formulae. When we look at the brain, we seem many levels of processing. It is believed that each level is learning features or representations at increasing levels of abstraction. For example, the standard model of the visual cortex suggests that the brain first extracts edges, then patches, then surfaces, then objects. The image shows how input in the eye leads to an action in a finger. And how the signal is processed in the brain in different processing centres. The eye does not see an object. Only after processing in different parts of the brain in the image V1, V2, V4, PIT, AIT, higher level object descriptions can be made.
- #42 This processing of a signal by a brain is more or less emulated in a Deep Learning Network. First line nodes are identified, then more advanced features. The advantage of this type of network is that they are more efficient than neural networks of twenty years ago. The algorithms are in open source available for Python, R == At CFT, twenty years ago, I had a state-of-the-art computer. A Dell 486 PC with a 66MHz processor and a 120 Megabytes Hard Drive. And I run the brainmaker software on this computer to train a neural network. Biggest problem in those days was to develop a working network topology. What was called pruning a network. That not only was working on a training set (relative easy to make a neural network that fits the data) but also worked for new data. Remember that I told that each fuzzy logic controller can be represented as a Neural Network. So twenty years ago I already tried to break the topology problem by using fuzzy sets and fuzzy logic rather than to do number crunching with a network. Deep Learning appears to be the current answer for developing better neural network topologies. Nowadays available hardware is much better. But you do not need any hardware anymore, as you can run algorithms on Spark and Hadoop clusters. Clusters that you do not have to buy, but that you just rent for the time you need it. For instance a 1000 elastic Spark cluster at Amazon EC2 (Elastic Cloud Computing). Typical current cost would be 5 USD per hour for a 50 Terabyte 10 node Cluster. Before you hire cluster time, you develop and test your algorithm. In the language you prefer, quants prefer R. On a local computer. When you are satisfied you bring the Gigabytes, Petabytes or Exabyte to Amazon (or a competitor) and run the algorithm. Hardware is not an issue anymore, money is not an issue anymore. For classification you can ire the Mechanical Turk.
- #43 I show an example of pattern recognition with a deep (belief) network by Geoffrey Hinton. Task for the network: Classify the number!
- #44 Without going into detail I show two clips from the Coursera Course Neural Networks for Machine Learning. The man in the window is professor Geoffrey Hinton, FRS, one of the leading scientist in Neural Networks. First Video is how a handwritten number is recognized by a layered neural network. So this way the network is used to recognize a pattern.
- #45 The second video shows how the network is used to generate handwritten numbers. I would call this artificial creativity. This way the network is used to generate new patterns. For the Crystal project this would be very nice feature, because at a certain point we want to generate new driving scenarios.
- #46 Andrew Ng of Stanford University and former leader of the google machine learning projects. Has the vision that deep learning involves the combination of the layered networtk approach in combination with big data. He gives the analogy: it is like bringing a rocket into orbit. You need a big engine (= a layered algorithm) fuelled by a lot of fuel (big data). Personally, I am a big fan of Andrew Ng and his ideas.
- #47 Big data analytics can be run on Spark and Hadoop. The table shows a benchmark between Spark and Hadoop. An example how a Spark Cluster processes a Petabyte in a matter of 4 hours. Developments are towards real time Big Data processing. By the way Spark and Hadoop is open source you can build your own small scale applications at your own PC. Or build a little cluster with some old PCs. Or hire time at Amazon EC2 Just to show you that it is there, you do not have to develop it, you don’t have to buy it.
- #48 The fuzzy oversteer model I presented, is what deep learners call a shallow model. It has no depth. There is no layering in it. And the model probably only works under specific conditions.
- #49 From the three dynamic traces (Lateral Acceleration Difference in Steering Wheel Angle, and Avz (Yaw rate)) a level of oversteer can be selected; These are the rules we need. However, it can lead to incorrect classification of oversteer in certain cases. For example, at low speeds the driver will tend to steer much more than at high speed; this can lead to a false indication of oversteer at parking lot speeds. Therefore, a strategy must be employed to only initiate a control action after a certain speed is attained. Also, when the oversteer-indicating fuzzy logic applies corrective braking, the vehicle dynamic response at the next time step is evaluated and usually gives a much lower level of oversteer as the correction helped stabilize the vehicle. To alleviate this problem of low speed control, a separate fuzzy logic structure using longitudinal speed (Vx) and lateral acceleration (Ay) to determine the level of a possible unstable event is used
- #50 So this was in effect our fuzzy algorithm.
- #51 The stability of an event can be described by a set of nine rules given above and based upon the inferred event stability, application of a oversteer assesment can follow, From the oversteer assessment a control action can be derived. Again we can plot a response surface for the input output relationship.
- #52 For this research, the oversteer level (0-10) was broken into three levels: no correction, moderate correction, and heavy correction. When the oversteer level was between 0 and 2, there will be no corrective action. When oversteer was indicated between 2 and 5.5, a moderate control strategy is employed. Finally, if the oversteer number is greater than 5.5, heavy correction is applied. No correction means no correction. Moderate correction, braking can be applied to the front left or right depending on the direction of the spin. This is determined in the fuzzy algorithm from the derivative of the yaw rate signal i.e., the yaw acceleration. The sign of the vehicle yaw angle reveals the direction of the spin and simple if/then statements are used to apply the braking force to the correct wheel (front left or front right). The braking torque is equal to the brake force times the effective rolling radius of the tire. Heavy correction, heavy correction is defined when the level of oversteer is greater than 5.5 In this case a ”large” braking torque is applied to the correct wheel to apply as much of a yaw moment as possible. This is the worst case if the controller reaches a very high oversteer level and as much control as possible needst o be applied to prevent a spin-out. The braking wheel must produce as much longituddinal force as possible to induce as much of a yaw moment as possible to cancel spin.
- #53 Examining the vehicle trajectories in Figure, it can be seen that the fuzzy logic ESC helped the vehicle track the lane change much better than without ESC or even the CarSim ESC. The yellow circles are cones placed upon the road. Above in meter, below in seconds. With no ESC or the CarSim ESC, the vehicle barely passed the lane change as it almost hit the last cone at x = 150m. The vehicle yaw moment gives an indication of the amount of brake force needed to be applied to slow or stop a spin.
- #54 Both the CarSim ESC and the fuzzy logic ESC stabilized the vehicle. This can be seen in Figure. Both ESC algorithms reduced the vehicle sideslip angle. The CarSim ESC lowered the maximum sideslip angle more than the fuzzy logic ESC; however, the fuzzy logic ESC damps out the sideslip angle more quickly. The fuzzy logic ESC dramatically decreased steering wheel angle (SWA) and, by extension, driver workload. Moreover, when the driver is traversing the second turn in the lane change (2.1 s), the CarSim ESC required more steering than without ESC or the fuzzy ESC. Lateral acceleration and yaw rate are similair to sideslip in the fact that the CarSim ESC produced smaller maximum values but the fuzzy logic ESC resulted in faster decays. It should be noted that the fuzzy logic ESC was tuned to work for all ten case studies while the CarSim ESC is specifically tuned for only this vehicle in this configuration. The CarSim ESC relies on accurate values of the cornering stiffness for the two degree-of-freedom vehicle model.
- #55 So we can see that in this example given in literature we more or less see a layered approach in coming from sensor data to the end driving more safely. It is not really deep learning algorithm, but the example conveys the concept of an approach we want to use for the Crystal project in case of safety classification.
- #56 So I want to go into the work that I am doing for the Crystal project and were I try to apply the principles I just demonstrated.
- #57 Objective is to find new scenarios in Driving Data eventually to evaluate safety of cooperative driving algorithms
- #58 Objective is to find new scenarios in Driving Data eventually to evaluate safety of cooperative driving algorithms
- #59 TNO works on the topic of autonomous and cooperative driving in the Automatic Driving Program. A milestone was achieved on 9 June (of this year) when our King and Minister Schulz van Haegen gat a demonstration of automatic cooperative driving. In the Crystal project we work on a topic were we look at safety of so-called scenarios and therefore we need to find scenarios in data. The objective is to evaluate safety of algorithms for collaborative driving without the need to drive 1o million miles to encounter all possibilities.
- #60 I can also classify data, based upon some supervised learning approach to train a neural network. The classifier in this specific example does not perform very well as I made an example set by hand and I think the lack of good performance is because I did not so good job in classifying 10000 examples by hand.
- #65 The general direction of the work is to create a deep learning network were the network topology is developed from a layered approach. Snapshots of sensor data are clustered into meaningful sequences. Typically in machine learning one uses sliding windows of different sizes. The sequences are identified, based upon similarities and a fuzzy classification. From the sequences one can derive scenarios. Making an emergency brake, lane change, making a crossing, etc. And a decision has to be made regarding the safety of a scenario.
- #66 This is the final knot we have to tie. We plan to bring the algorithm to a Spark cluster that was set up for the Crystal project. So we can practice deep learning on this cluster. An learning algorithm fuelled with big data
- #67 So I hope it makes sense to you, why I wanted to use fuzzy logic again after twenty years. I think it is suitable for solving a complex scenario classification problem at hand. And use it to generate new scenarios with a working networks. Collaborative driving is complex and a crisp analytic approach is probably not suitable for solving the problem. === Scientifically speaking there is a controverse between some of the mathematicians working on this problem. They think that doing Monte Carlo is enough for analyzing the robustness of safety algorithm. I think that the approach of generating scenarios with an deep neural network is better (it should be more than epistemic – may be even aleatoric) That is the part of the work that is of scientific interest.
- #68 I think that using fuzzy logic in a layered approach can help with building topologies for layered (deep learning) network: I hope to demonstrate the following benefits in the Crystal project Work with Expert input without need for exact models Work with imprecise data Easier to develop layered topologies using Fuzzy Logic Better understanding what it does Possible to create neural networks Generate new scenarios with the neural network I set up this colloquium as I wanted to get more structure my thought about using fuzzy logic in a deep learning algorithm I hope you enjoyed the result of this structuring process, at least you now what Hadoop is.