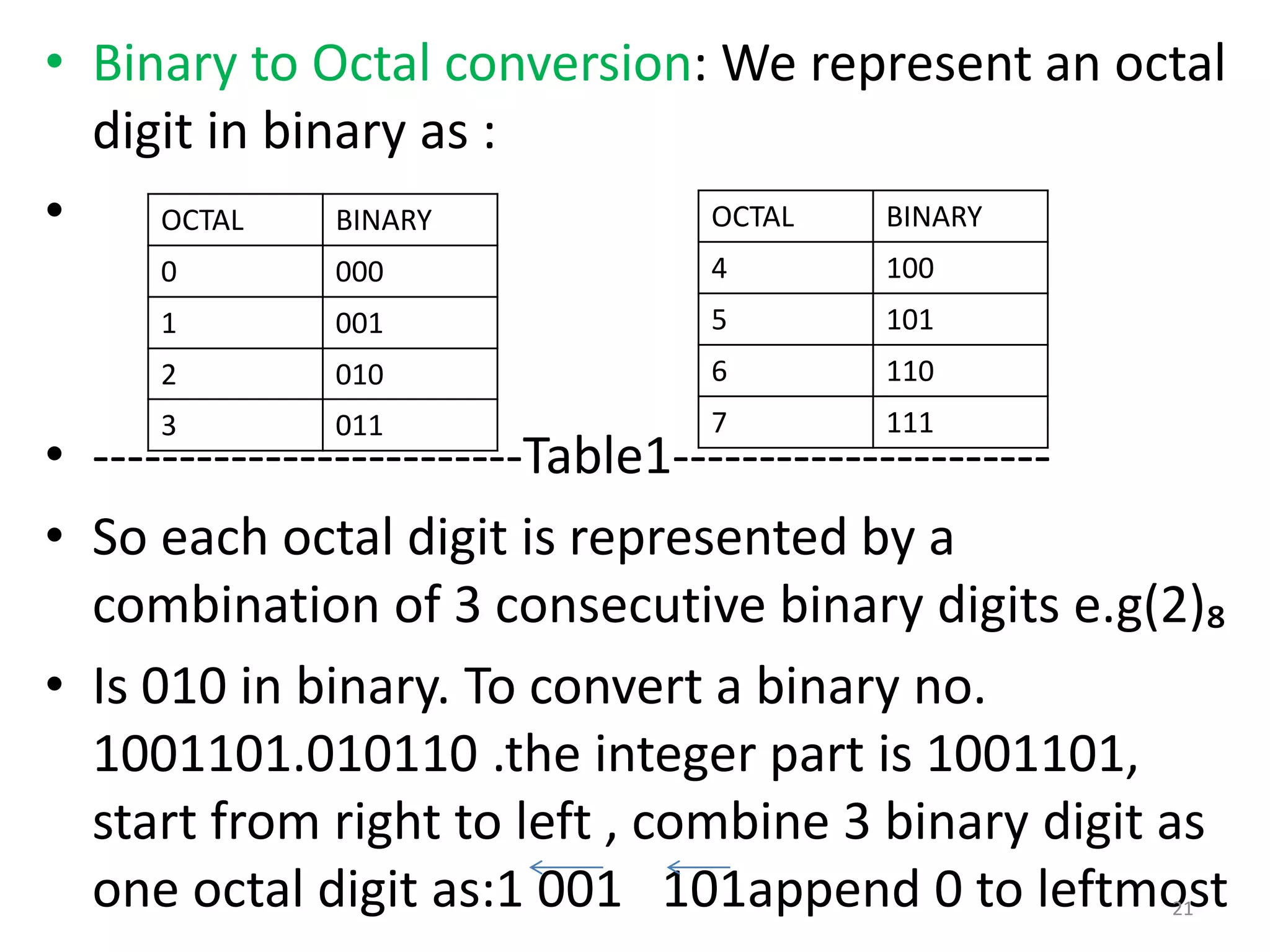
This document discusses different number systems including binary, octal, decimal, and hexadecimal. It provides examples of how to represent a number in each system and how to convert between them. The key points covered are: 1) Positional number systems assign a place value to digits based on their position, while non-positional systems do not. 2) Binary uses digits 0 and 1. Octal uses digits 0-7. Hexadecimal uses digits 0-9 and A-F. 3) To convert a decimal number to another base, it is repeatedly divided by the new base and the remainders are used to build the number in the target base from right to left.

1. Digital Electronic
A III semester course in Digital
Electronics.
Topic 1 Number System
BY Vinod Kataria(VK)
1

2. CONTENTS
• Number system
• Non Positional and Positional number System
• Binary Number System
• Octal Number System
• Hexadecimal Number System
• Relationship between Hexadecimal, Octal,
Decimal, and Binary
• Number Conversions
2

3. Number system
• A number system is a representation of a
number say one, two, etc.
• Two types of number system
1) Non positional number system.
2)Positional number system.
3

4. • Non Positional: Roman number system is non
positional system since a separate symbol is
used to represent a value.(I V X L C D & M)
• (I = 1, V = 5, X = 10, L = 50, C = 100, D = 500 and
M = 1000), are the symbols used to represent
values in this system.
• If I write VV then it is not equal to 55. i.e. vv not
= 55. Look here V retains its value as 5
irrespective its position, so VV is 5 &5. For 55
LV is written.
• Hence in Roman system, value of a symbol does
not change with its position.
4

5. • Positional number system: Have a look
• 5 is a number in a system. If I write 55 in this
system then the number at arrow is not 5
instead it is 50. The value of 5 changes according
to its position . Same 5 will become 500 in 555 .
• Number systems which allow such
representation are positional number system.
• Such positional systems are also called weighted
system. Values associated to the number will
depend on its position and value of the total
number is sum of such associated values of each
number.
5

6. Normally a value of a number in a positional
number system is defined by the expression:
xn * rn + xn-1 * rn-1 +----------------------+ x0 * r0
e.g. Value of a number 5456 is calculated as :
5*103 +4*102 +5*101 +6*100 = 5000+400+50+6
= 5456. in decimal number system which is
positional number system.
Here r is called radix or base of the number
system.
A digit is defined in the positional number system
which defines the position of the number in the
number system , look at the above number
6

7. 5456, the 6 is at first position which is called unit in
decimal number system, immediate 5 is ten, 4 is
hundred and 5 is thousand. Also observe here that
value of number 5 here changes according to its
position for 50 to 5000.The unit is a digit . Similarly
ten , hundred and thousand are also digits.
A digit consist of numbers starting from 0 up to
radix r -1. so a digit in decimal number system will
have 0,1,2,-----,8,9. The maximum number is 9 i,e,
radix which is 10-1 is 9.
Value of the digit is called its weight.
7

8. • The weight is called radix r.Recall again the
expression:
• So rn is the weight of the nth digit and xn
*weight is the decimal value of the digit.
• positional systems will have a base . Non
positional systems will not have base.
• Types of positional number system:
– Decimal(as defined in previous slide)
– Binary
– Octal
– Hexa decimal
– Other number systems based on radix r.
xn * rn + xn-1 * rn-1 +----------------------+ x0 * r0
8

9. • Binary Number System:
• Its base (radix r) is =2. hence its each digit will
have only two number either 0 or 1(radix r-1 =
2-1=1).
• Expression : where
r=2. so a binary number 011011100 which is a
9 digit number and weight of each digit is based
on 2(20 , 21 , 22 and so on up to 28 ).
• The 9 digit no. will be represented as:
• 0*28+1*27+1*26+0*25+1*24+1*23+1*22+0*21+0
*20 .
xn * rn + xn-1 * rn-1 +----------------------+ x0 * r0
9

10. • Octal Number System:
• Its base (radix r) is =8. hence its each digit will
have numbers from 0,1,------7(radix r-1 = 8-1=7).
• Expression : where
r=8. so an Octal number 275 which is a 3 digit
number and weight of each digit is based on 8(80
, 81 ,and 82 ).
• The 3 digit no. will be represented as:
• 2*82+7*81+5*80 .
xn * rn + xn-1 * rn-1 +----------------------+ x0 * r0
10

11. • Hexadecimal(HEX) Number System:
• Its base (radix r) is =16. hence its each digit will
have numbers from 0,1,------9 and A,B,C,D,E,F
(radix r-1 = 16-1=15).here value of A is decimal
10, B is decimal 11 and so on F is decimal 15.
• Expression : where
r=16. so an HEX number 5B8 which is a 3 digit
number and weight of each digit is based on
16(160 , 161 ,and 162 ).
• The 3 digit no. will be represented as:
• 5*162+11*161+8*160 .
xn * rn + xn-1 * rn-1 +----------------------+ x0 * r0
11

12. • The number systems defined in previous slides
are commonly used number system , but one can
use any type of positional (weighted) number
system by defining its base(radix r) and by
following the expression given in previous slides.
• Different type of number system (such as radix 5,
radix11) will be studied by us in later section of
the course.
12

13. • Representation of a number in different number
systems:Any number can be represented in two
form 1) integer and 2) fraction. Integer will not
have a decimal(dot . ) in the number while
fraction contains dot (.) to separate integer part
and fractional part.
• Consider a number 245.35 it is a combination of
3 digit integer and two digit fraction. Using
formula
The number is represented as:
• 2*102 +4*101 +5*100 = 200+45+5= 245 as
integer part of Decimal system
xn * rn + xn-1 * rn-1 +----------------------+ x0 * r0
13

14. • While (.35) will be represented as:
• 3*1/100 + 5*1/101 = .30 + .05 = .35. so the
number is represented as 245.35 in decimal
number system.
• Same number will have different representation
in Binary coded number system. In this number
system every digit of the number is first
represented by number of binary digits since any
number >1 can not be accommodated in one
digit binary digit. Hence
• 2 is first represented as 10(1*21 + 0*20 = 2+0=2).
• 4 is represented--100(1*22+0*21+0*20=4+0+0=4)
14

15. • 5 is represented- 101(1*22+0*21+1*20=4+0+1= 5).
So the integer is 001001000101. This
representation is binary coded decimal (we will
study it in detail later). This is integer part of the
number.
• The fraction part is: 3 is represented as 011(0*22
+1*21 +1*20 =0+2+1=3) and 5 is 101(1*22 +0*21
+1*20 =4+0+1=5). So the no. is (.00110101).
• To represent the same number 245.35 in binary
number system we have to convert this number
into its binary equivalent. Similarly for octal and
hex.
15

16. • Conversion of a decimal number to binary
number: Integer part of the number is divided by
two , i.e. 245 of previous number is divided by 2
we get 245/2=122as quotient and 1 as remainder
. The remainder is accumulated and quotient is
further divided to get 122/2=61 and reminder
=0.this is continued till full number is not
exhausted as
• 245/2=122 and 1 LSB
• 122/2=61 and 0
• 61/2=30 and 1
• 30/2=15 and 0
16

17. • 15/2=7 and 1
• 7/2=3 and 1
• 3/2=1 and 1
• ½=0 and 1 MSB
• The accumulated remainder is written as
• 11110101
• Last reminder is MSB of binary number and first
remainder is LSB. So 245 is written as 11110101.
• The fraction part .35 will be converted as:
• The fraction is multiplied by 2 to get .35*=0.70,
the digit before decimal,0 is collected and the
product is again multiplied by 2 to get :
17

18. • .70*2=1.40 , accumulate 1 and multiply .40 by 2
to get 0.80, accumulate 0 and multiply .80 *2 to
get 1.60 accumulate 1 and repeat same till you
find a repetition of cycle. The accumulated
number till now is 0101 so the number is .01011
• Addition of integer and fraction will give the
number as 11110101.01011
• Conversion of a binary number into decimal
number : we will use the formula
• 1*27+1*26+1*25+1*24+0*23+1*22+0*21+1*20=245
as integer part and 0*2-1+1*2-2+0*2-3+1*2-4+1*2-5
=35 as fraction. The number is 245.35
xn * rn + xn-1 * rn-1 +-+ x0 * r0
18

19. • Conversion of a decimal number into octal & hex
• Octal has base(radix) = 8 and Hex has 16. As we
did in binary number conversion do the same.
Division in binary was done by 2 since its base was
2 , so now division is by 8 & 16 respectively.
• Octal: divide 245 by 8 and accumulate remainder
245/8=30 and R is 5. LSB
• 30/8=3 and R is 6,
• 3/8=0 and R is 3. MSB so integer part of
• octal number is 365 and fraction is 0.35*8=2.8 So
A is 2 , .8*8=6.4 so A is 6, .4*8=3.2 so A is 3 we get
.263. Hence the no. is 365.263 19

20. • Hex: divide 245 by 8 and accumulate remainder
• as: 245/16=15 , R is 5.
• 15/16=0 , R is 15 (F). Integer Hex is F5
• fraction is 0.35*16= 5.6 so A is 5 , .6*16=9.6 ,A is
9, .6*16=9.6 ,R is 9 and so on we get .599. Hence
the no. is F5.599.
• Representation of these numbers with their base:
• Decimal(245.35)₁₀
• Binary(11110101)₂
• Octal(365.263)₈
• Hex(F5.599)₁₆
• General way of writing base is (number)r.
20

21. • Binary to Octal conversion: We represent an octal
digit in binary as :
•
• -------------------------Table1----------------------
• So each octal digit is represented by a
combination of 3 consecutive binary digits e.g(2)₈
• Is 010 in binary. To convert a binary no.
1001101.010110 .the integer part is 1001101,
start from right to left , combine 3 binary digit as
one octal digit as:1 001 101append 0 to leftmost
OCTAL BINARY
0 000
1 001
2 010
3 011
OCTAL BINARY
4 100
5 101
6 110
7 111
21

22. • Digit if it is less than 3. so the combination is
• 001 001 and 101. From the table 001 is 1 and 101
is 5 , so octal number is (115)₈ (integer part)
• For fraction combination is done from left to
right.so .010110 = .010 110,from table it is(.26)₈
• The octal no. is (115.26)₈ .
• Same binary no. can be converted into Hex :
• ---------------------Table 2 ---------------------------------
HEX BINARY
0 0000
1 0001
2 0010
3 0011
HEX BINARY
4 0100
5 0101
6 0110
7 0111
HEX BINARY
8 1000
9 1001
A 1010
B 1011
HEX BINARY
C 1100
D 1101
E 1110
F 1111
22

23. • The combination is 4 binary digit instead of 3(as
done in octal) . Hence the binary number
1001101.010110 is converted as
• 1001101 = 0100 (append 0 at the left) and
1101 . From table 2 0100=4 and 1101=B so
integer part is (4B)₁₆ and fraction .010110 =
.0101 1000(append 00) = .58(from table 2) so
the Hex no. is (4B.58)₁₆ .
• Octal and Hex to Binary conversion:
• Each digit of each octal and hex no. is first
converted into binary digits then append these
digits from MSB to LSB to form the respective
number as: 23

24. • The number (115.26)₈ .write each digit into its
binary equivalent , so 1=001, 1=001 , 5=101 so
integer part is 001001101 and fraction is .010 110
• So Binary no. is 001001101.010110. remove left
most 0s from integer and right most 0s in fraction
the final binary is (1001101.01011)₂ . Similarly
the Hex no.is converted to Binary.The No.(4B.58)₁₆
• 4=0100 and B=1101, 5=0101 and 8=1000 so the
number is 01001101.01011000. remove 0s from
leftmost of integer and right most of fraction so
number is (1001101.01011)₂ .
24

25. 25