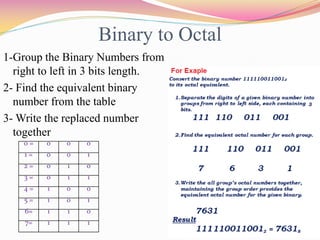
The document outlines the topic of number systems, covering binary, octal, decimal, and hexadecimal formats. It provides detailed methods for converting between these systems, along with examples for clarity. Additionally, it discusses binary arithmetic operations including addition, subtraction, multiplication, and division.

1. Saeed Ullah Jan
(PhD – Scholar University of Malakand)
Lecturer in Computer Science
Govt Degree College Wari (Dir Upper)
Email: saeedullah@uom.edu.pk // saeedjan03@gmail.com
Phone: 0944-840488
Course Title: Digital Logic & Computer Design
Program: BS – Computer Science 3rd Semester

2. Number System
 Number System
Symbols using for counting numerical quantities or measure
 Common Number System
1) Binary (0,1) also called base 2 like (1001101) 2
2) Octal (0,1,2,3,4,5,6,7) base 8 like (5446) 8
3) Decimal (0,1,2,3,4,5,6,7,8,9) base 10 like (742869) 10
4) Hexadecimal (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F) base 16 like (18AF9)16
 Conversion
Before going to this section, the tables in next slide must be
remember to everyone

3. 0 0 = 0
0 1 = 1
1 0 = 2
1 1 = 3
• For two Binary Numbers, all the
possible combinations are as under
n=2 and 2n = 22 = 4
• For Three Binary Numbers, all the
possible combinations are as under
n=3 and 2n = 23 = 8
0 0 0 = 0
0 0 1 = 1
0 1 0 = 2
0 1 1 = 3
1 0 0 = 4
1 0 1 = 5
1 1 0 = 6
1 1 1 = 7
• For Four Binary Numbers, all the
possible combinations are as under
n=4 and 2n = 24 = 16
0 0 0 0 = 0
0 0 0 1 = 1
0 0 1 0 = 2
0 0 1 1 = 3
0 1 0 0 = 4
0 1 0 1 = 5
0 1 1 0 = 6
0 1 1 1 = 7
1 0 0 0 = 8
1 0 0 1 = 9
1 0 1 0 = A
1 0 1 1 = B
1 1 0 0 = C
1 1 0 1 = D
1 1 1 0 = E
1 1 1 1 = F

4. Binary to Octal
1-Group the Binary Numbers from
right to left in 3 bits length.
2- Find the equivalent binary
number from the table
3- Write the replaced number
together
0 = 0 0 0
1 = 0 0 1
2 = 0 1 0
3 = 0 1 1
4 = 1 0 0
5 = 1 0 1
6= 1 1 0
7= 1 1 1

5. Binary to Decimal
1) Multiply each binary number with 2
2) Each binary multiplication number with 2 will add with the next binary number
multiplication with 2
3) Assign power on two from right to left
4) Follow ordinary mathematical method and at the end add all the digits
Example:
(110011)2=()10?
(110011)2= 1x25+1x24+0x23+0x22+1x21+1x20
(110011)2=32+16+0+0+2+1
(110011)2=(51)10
(101101)2=()10?
= 1x25+0x24+1x23+1x22+0x21+1x20
=1x32+0x16+1x8+1x4+0x2+1x1
= 32+0+8+4+0+1
= (45)10

6. Binary to Hexadecimal
1-Group the Binary Numbers from right to left in 4 bits length.
2- Find the equivalent binary number from the table
3- Write the replaced number together
0 0 0 0 = 0
0 0 0 1 = 1
0 0 1 0 = 2
0 0 1 1 = 3
0 1 0 0 = 4
0 1 0 1 = 5
0 1 1 0 = 6
0 1 1 1 = 7
1 0 0 0 = 8
1 0 0 1 = 9
1 0 1 0 = A
1 0 1 1 = B
1 1 0 0 = C
1 1 0 1 = D
1 1 1 0 = E
1 1 1 1 = F

7. Octal to Binary
step 1: Separate the digits of the given octal number,
if it contains more than 1 digit.
step 2: Find the equivalent binary number for each
digit of octal number. Add 0's to the left if any of the
binary equivalent is shorter than 3 bits.
step 3: Write the all group's binary numbers
together, maintaining the same group order provides
the equivalent binary for the given octal number.
For Example: Convert the octal 76318 to its binary
equivalent.
0 0 0 = 0
0 0 1 = 1
0 1 0 = 2
0 1 1 = 3
1 0 0 = 4
1 0 1 = 5
1 1 0 = 6
1 1 1 = 7

8. Octal to Decimal
Step 1:Take the given octal number.
Step 2: Find out the number of digits in the number
Step 3: Let it have n digits.
Step 4: Multiply each digit in the number with 8n-1,when the digit is in the
nth position.
Step 5: Add all digits after multiplication.
Step 6: The resultant is the equivalent decimal to the given octal number.
If octal number contains a decimal point
Step 7: Let m digits are there after the decimal
Step 8: Multiply each digit after decimal with ,when the digit is the nth
position.
All other steps are same as above.
Question 1: Convert 57468 to decimal number
Solution:
The given number is 57468
57468 = (5 x 83)+ (7 x 82) + (4 x 81) + (6 x 80)
=5 x 512 + 7 x 64 + 4 x 8 + 6 x 1
= 2560+448+32+6
= 3046
The equivalent decimal number for 57468 is 3046
57468 = 3046

9. Octal to Hexadecimal
Step 1: Let the number of digits in the number be n
Step 2: Multiply the digits with 8n-1where n is position of digit from the right
end of the number. If the number has decimal part the multiply digits after
decimal by where m is position of the number from the decimal
Step 3: Add the terms after multiplication
Step 4: The obtained number is equivalent decimal number to the given octal
Step 5: Consider the decimal number, divide it by 16
Step 6: Note the remainder.
Step 7: Continue the process till the quotient in zero
Step 8: Write the remainder in the reverse order
Step 9: The obtained number is equivalent hexadecimal number
to the given octadecimal number.
Example:
(715)8=()16?
(715)8=(111,0001,0101)2
(715)8=(0001,1100,1101)2
So
(715)8=(1CD)16
0 0 0 0 0
0 0 0 1 1
0 0 1 0 2
0 0 1 1 3
0 1 0 0 4
0 1 0 1 5
0 1 1 0 6
0 1 1 1 7
1 0 0 0 8
1 0 0 1 9
1 0 1 0 A
1 0 1 1 B
1 1 0 0 C
1 1 0 1 D
1 1 1 0 E
1 1 1 1 F

10. Decimal to Binary
To convert integer to binary, start
with the integer in question and
divide it by 2 keeping notice of
the quotient and the remainder.
Continue dividing the quotient by
2 until you get a quotient of zero.
Then just write out the
remainders in the reverse order.
For Example
(156)10 = (?)2
= (10011100)2

11. Decimal to Octal
Step 1: Take the given decimal number
Step 2: If the number is less than 8 the octal number is the same
Step 3: If the number is greater than 7 then Divide the number with 8
Step 4: Note the remainder
Step 5: Carry on the step 3 and 4 with the quotient till it is less than 8
Step 6: Write the remainders in reverse order(bottom to top)
Step 7: The resultant is the equivalent octal number to the given
decimal number Examples:

12. Decimal to Hexadecimal
 Divide the decimal number by 16. Treat the division
as an integer division.
 Write down the remainder (in hexadecimal).
 Divide the result again by 16. Treat the division as an
integer division.
 Repeat step 2 and 3 until result is 0.
 The hex value is the digit sequence of the remainders
from the last to first.
DIVISION RESULT
REMAIN
DER (in
HEX)
256 / 16 16 0
16 / 16 1 0
1 / 16 0 1
ANSWER 100
Example 1
Convert the number 256 DECIMAL to HEXADECIMAL
DIVISION RESULT
REMAINDER
(in HEX)
921 / 16 57 9
57 / 16 3 9
3 / 16 0 3
ANSWER 399
Example 2
Convert the number 921 DECIMAL to HEXADECIMAL
DIVISION RESULT
REMAINDER
(HEX)
100 / 16 6 4
6 / 16 0 6
ANSWER 64
Example 3
Convert the number 100 DECIMAL to HEXADECIMAL
DIVISION RESULT
REMAINDER
(HEX)
590 / 16 36 E (14 decimal)
36 / 16 2 4 (4 decimal)
2 / 16 0 2 (2 decimal)
ANSWER 24E
Example 4
Convert the number 590 DECIMAL to HEXADECIMAL

13. Hexadecimal to Binary
Use the table and convert hexadecimal to
binary easily.
Example:
(1AD)16=(?)2
 The binary value for 1 in the table is 0001
 The binary value for A in the table is 1010
 The binary value for D in the table is 1101
 Now, from this we can easily solve, the given
example
(000110101101) is the equivalent of (1AD)16 or
Simply 110101101)2 = (1AD)16
0 0 0 0 = 0
0 0 0 1 = 1
0 0 1 0 = 2
0 0 1 1 = 3
0 1 0 0 = 4
0 1 0 1 = 5
0 1 1 0 = 6
0 1 1 1 = 7
1 0 0 0 = 8
1 0 0 1 = 9
1 0 1 0 = A
1 0 1 1 = B
1 1 0 0 = C
1 1 0 1 = D
1 1 1 0 = E
1 1 1 1 = F

14. Hexadecimal to OctalStep 1: Consider the given hexadecimal number
Step 2: First count the number of digits in the number
Step 3: If n is the position of the digit from the right end then multiply each digit with 16n-1
Step 4: Add the terms after multiplication
Step 5: Resultant is the equivalent decimal form
Step 6: Divide the decimal number with 8
Step 7: Note down the remainder
Step 8:Continue step 6 and 7 with the quotient, until the quotient is zero
Step 9: Write the remainders in reverse order
Step 10: The obtained number is the required result.

15. Hexadecimal to Decimal
 To convert a hexadecimal to a decimal manually, you must start by multiplying the hex number by
16. Then, you raise it to a power of 0 and increase that power by 1 each time according to the
hexadecimal number equivalent.
 We start from the right of the hexadecimal number and go to the left when applying the powers.
Each time you multiply a number by 16, the power of 16 increases.
For Example
(2A9)16 = (?)10
= 2x162 + A(10)x161 + 9x160
= 2x256 + 10x16 + 9x1
= 512 + 160 + 9
= 681
Therefore, (2A9)16 = (681)10
Another Example
(5F3C)16 = (?)10
= 5x163 + F(15)x162 + 3x161 + C(13)x160
= 5x4096 + 15x256 + 3x16 + 13x1
= 2096 + 3840 + 48 + 13
= 5997
Therefore, (2A9)16 = (5997)10

16. Binary Arithmetic
The arithmetic of binary numbers means the operation of addition, subtraction,
multiplication and division. Binary arithmetic operation starts from the least significant
bit i.e. from the right most side. We will discuss the different operations one by one in the
following article.
1) Binary Addition
There are four steps in binary addition, they are written below:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 (carry 1 to the next significant bit)
Example

17. 2) Binary Subtraction
Here are too four simple steps to keep in memory 0 - 0 = 0
0 - 1 = 1, borrow 1 from the next more significant bit
1 - 0 = 1
1 - 1 = 0
A binary arithmetic example is given to understand the operation more clearly
Suppose, A = 10101100 and B = 1010100 and we want to find out A - B. Now implementing
the rules of binary subtraction
Here 0 - 1 = 1 with borrowing of 1 from the next significant
bit and that’s what has been done. We will treat the next 1
as 0 in the next step as shown below.
Again the last 1 has been borrowed because the operation
done was 0 - 1 = 1 with borrow 1 from the next most
significant bit and the final result of binary subtraction,
we got is written in the place of result in the final step.

18. 3) Binary Multiplication
binary multiplication there are also four steps to be followed during a bigger
multiplication or we can say these fundamental steps as well.
Example
10101101x1101 = 10101101
1101
____________________________
10101101
00000000x
10101101xx
10101101xxx
_______________________________
Now, using simple addition method, x means nothing blank or consider it zero
=100010001011

19. 4) Binary Division
Though it is not too much difficult, it may look a bit tougher than the other binary
operations because all the other had some similarity among themselves like they all had
four basic steps which made all the processes quiet easy to understand but the binary
division process does not have any specific rule to follow. Though this process is quite
similar to the decimal division. The process will not be clear until we look at an example.
Let us take A = 11010 and B = 101
In this step 101 is subtracted from 110. This step is also
very easy to understand as we already know binary
subtraction method. Now going into the next step.
As of the rules of division the next least significant bit comes down and
we try to multiply 1 with divider i.e. B but the result is bigger than the
minuend so this step cannot be completed and we have to go to the
next step.
In the final step binary subtraction is
done and we get the remainder and the
operation of binary division is
completed and we get the following
result. Quotient = 101 and remainder = 1.

20. Binary Complementation
In binary system there are only two digits 0 and 1. In binary
system each and every number and its sign are represented
by using only these two digits 0 and 1. As the negative and
positive signs can not be written directly in binary system, we
have to find some alternative method of representing them.
1) 1’s Complement
The complement of 0 is 1 and 1 is 0, let suppose
The 1’s complement of 1101101 is 0010010
And
0001010110101000 is 1110101001010111

21. 2) 2’s Complement
If, 1 is added with the answer of 1’s complement, then it is
said to be the 2’s complement of the said binary number, for
example the 2’s complement of 0000 0101, we have to find
the 1’s complement of 0000 0101 which is 11111010 and then
add 1 with it like

22. 3) 9’s Complement
To obtain the 9's complement of any number we have to
subtract the number with (10n - 1) where n = number of
digits in the number, or in a simpler manner we have to
divide each digit of the given decimal number with 9. The
9’s Complement of 456 is given below:

23. 3) 10’s Complement
Now coming to 10's complement, it is relatively easy to find out the 10's complement
after finding out the 9's complement of that number. We have to add 1 with the 9's
complement of any number to obtain the desired 10's complement of that number. Or
if we want to find out the 10's complement directly, we can do it by following the
following formula, (10n - number), where n = number of digits in the number. An
example is given below to illustrate the concept of obtaining 10’s complement. Let us
take a decimal number 456, 9's complement of this number will be:
is the 10’s complement of 456