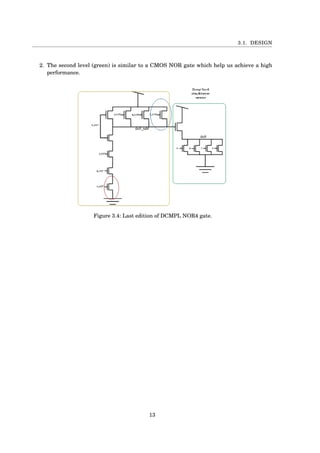
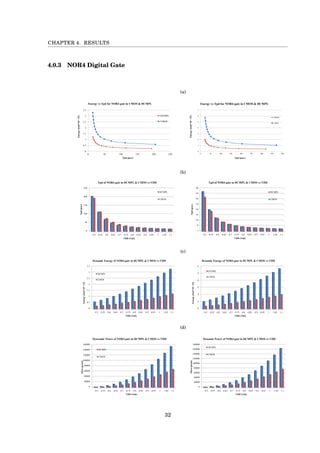
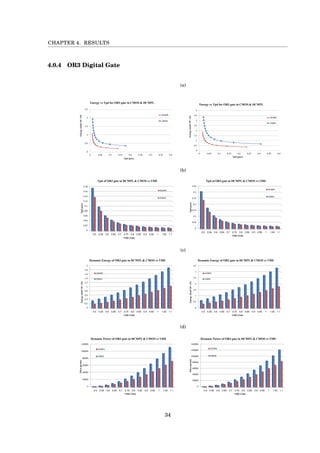
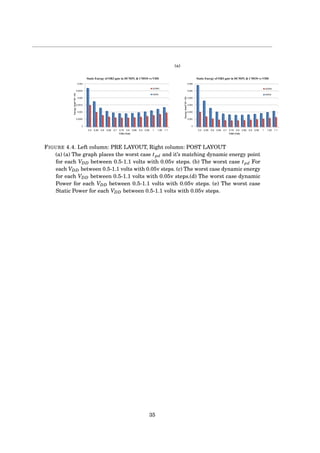
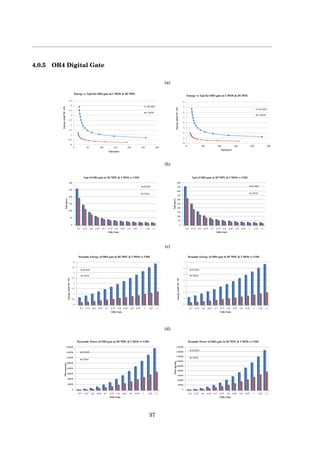
This document presents a project book on designing DCMPL logic circuits in a 28nm process technology. It was authored by Itamar Greenberg and Shay Rubinstein from the Department of Electrical Engineering at Bar Ilan University. The document includes an introduction to CMOS scaling challenges, a literature survey of logic families such as diode logic, RTL, TTL, NMOS, PMOS and CMOS. It describes the design, modeling, layout and simulation of various digital logic gates including NOR3, NOR4, OR3 and OR4 gates. Simulation results on propagation delay, energy consumption, voltage transfer curves and noise margins are presented and analyzed.

1. Bar Ilan University
Project Book:
DCMPL Logic Circuits Technique in
a 28nm Process Technology
By
ITAMAR GREENBERG
SHAY RUBINSTEIN
Department of Electrical Engineering
BAR ILAN UNIVERSITY
SEPTEMBER 2016

3. TABLE OF CONTENTS
Page
List of Tables ii
List of Figures iii
1 Introduction 1
1.1 History . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
2 Literature Survey 3
2.1 Logic Families . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
3 Design and Simulation 9
3.1 Design . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.1.1 NOR Digital Logic Gate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.2 Modeling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
3.3 Layout . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.4 Simulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3.4.1 Propagation Delay (tpd) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3.4.2 Dynamic &. Static Energy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
3.4.3 "SNM"- Static Noise Margin . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.4.4 "VTC"- voltage transfer curve simulation . . . . . . . . . . . . . . . . . . . . 25
3.4.5 "NM"- noise margin simulation . . . . . . . . . . . . . . . . . . . . . . . . . . 26
4 Results 27
4.0.1 Summery Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
4.0.2 NOR3 Digital Gate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
4.0.3 NOR4 Digital Gate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
4.0.4 OR3 Digital Gate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
4.0.5 OR4 Digital Gate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
4.1 VTC-voltage transfer curve . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
4.1.1 CLASIC SIMULATION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
4.1.2 MONTE CARLO SIMULATION . . . . . . . . . . . . . . . . . . . . . . . . . . 41
4.2 Noise Margin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
5 Summary & Conclusions 43
i

4. Bibliography 45
LIST OF TABLES
TABLE Page
3.1 NOR digital gate characteristic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.2 Characteristic table design . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
ii

5. LIST OF FIGURES
FIGURE Page
1.1 CMOS parameters during scaling. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2.1 Diode logic OR gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2 RTL not logic gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.3 RTL NOR3 logic gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.4 TTL NOR logic gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.5 NMOS NOR logic gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.6 PTL MUX gate uses only two transistors . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.7 Transmission gate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.8 CMOS NAND and NOR logic gates. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
3.1 CMOS NOR4 gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.2 First edition of DCMPL NOR4 gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3.3 Second edition of DCMPL NOR4 gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
3.4 Last edition of DCMPL NOR4 gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.5 NOR gate design with different fan in inputs . . . . . . . . . . . . . . . . . . . . . . . . . 14
3.6 CMOS and DCMPL modelling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.7 The deplorable input vector in our design . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
3.8 Layout Challenges in 28 nm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.9 A visual representation of tPHL &. tPLH . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3.10 A chain of six NOR2 gates connected through input ’A’. . . . . . . . . . . . . . . . . . . 21
3.11 The chain from the previous example is now a unified instance. . . . . . . . . . . . . . 21
3.12 A typical waveform returned by the ’getPower’ function. In reality the peaks are much
more narrow. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3.13 A zoomed in view of the ’getPower’ peak. . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
3.14 Hair-forming mutant cells. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.15 Transform Nor2 gate to inverter with 2 inputs in ring oscillator configuration. . . . . 25
3.16 Measuring noise margin from "VTC" curve. . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.17 Measuring noise margin from "VTC" curve. . . . . . . . . . . . . . . . . . . . . . . . . . . 26
4.1 Summery Results. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
4.2 Energy vs tpd simulation-NOR gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
4.3 Energy vs tpd simulation-NOR gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
4.4 Energy vs tpd simulation-OR gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.5 Energy vs tpd simulation-OR gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
4.6 The deplorable input vector in our design . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
4.7 VTC graph for NOR3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
iii

6. LIST OF FIGURES
4.8 Monte Carlo 1500 points nor3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
4.9 NM simulation NOR gate. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
iv

7. CHAPTER
1
INTRODUCTION
F
or over four decades scientists have been scaling increasingly smaller devices trying to
maintain the "MOORE" law. This trend caused by unending demand for high performance
appliances such as laptops, cellphones, and "IOT"-internet of things. Another challenge
these days is dealing with growing competition between the chip design companies. No matter
how the future of the VLSI world will look like one steady rule will stay: It is impossible to
improve power consumption, performance, and area of the chip at the same time. Or in other
words: "there is no free lunch". In this chapter we describe the main issues that concern engineers
dealing with the CMOS unreliability problems in process and integrating IP’s for nanometer
technology. The intent of this chapter is not to give an in-depth description of the failure behind
the problems, but to provide the reader with the basic knowledge of CMOS reliability problems
and how they affect the performance at gate level circuit. First, sec 1.1 outlines how various
unreliability effects came into play in the course of history. Later sec 1.2 we will briefly explain
the mainstream unreliability effects such as spatial unreliability effects and time-dependent
unreliability effects.
1.1 History
The reliability of digital devices was first studied in the 1960’s, when complex integrated systems
were developed for the first time. The most famous conference which brought the physical unre-
liability problem to light was the first international reliability physics symposium (IRPS 1962,
Chicago).
During the 1970’s effects such as ionic contamination and corrosion were the most common causes
of circuit failure. During the 1980’s integrated reliability issues became visible. Further scaling
of the oxide thickness had increased the electrical field between the gate and the bulk, which
creates the hot carries injection phenomenons that eventually harm the gate performance.
Initially, arbitrary voltage stress resulted in an identical parameter shift for matched devices [5].
So at the beginning this kind of unreliability effects were considered as deterministic problems.
However, when oxide dielectrics reached the atomic- scale dimension, it resulted in the first
stochastic temporal unreliability effect. In the late 1980’s when the dimensions of the devices
1

8. CHAPTER 1. INTRODUCTION
Figure 1.1: CMOS parameters during scaling. Figure reproduced from [? ].
had scaled to the nanometeric realm, stochastic errors and variations at the atomic level became
apparent at device level and sensitive analog circuits were the first to suffer from process vari-
ability effects (Lakshmi Kumar et al. 1986; Pelgrom et al. 1989).
Device mismatch became a big issue (especially analog) designers had to deal with in order to
guarantee good accuracy and high yield.
2

9. CHAPTER
2
LITERATURE SURVEY
D
igital logic gates are the building blocks of a digital integrated circuit (IC). In order to
improve our IC performance while maintaining its size, the logic gate will be a good place
to start. In this chapter we review the evolution of the logic gate through the frame of the
logic family.
2.1 Logic Families
In order to produce an IC one can use different configuration and fabrication methods. Each of
these methods is a specific logic family. The idea of using a specific logic family when producing
ICs is to be able to have a similar electrical characteristics between different devices. Those
characteristics are supply voltage range, speed of response, dissipation of power, input and output
logic levels, noise margin, fan-out, currents etc.
Logic families are usually divided by the type of transistor they use, in our case bipolar and Metal-
Oxide-Semiconductor (MOS) transistors. The main bipolar families are diode logic (DL), emitted
coupled logic (ECL), resistor transistor logic (RTL), diode transistor logic (DTL), transistor-
transistor logic (TTL). Main members of the MOS family are Pass Transistor Logic (PTL), P-type
MOS (PMOS), N-type MOS (NMOS) and Complimentary MOS (CMOS). Each of these logic
families has multiple variations and tweaks that improve certain aspects of the logic family. Some
of these variations are considered as different logic families all together. By and large, there can
be hundreds of different logic families one can use to produce a logic gate or an IC.
Understanding the principles of various logic families can help us when trying to produce a new
logic family. We review some of the logic families mentioned above.
3

10. CHAPTER 2. LITERATURE SURVEY
Diode Logic
The first logic family we will discuss uses diodes and resistors to implement Boolean logic gates.
It was used in old computers to replace vacuum tubes (1950’s).
The DL OR gate is implemented in figure 2.1. If one of the two inputs is a logic ’1’ then the
corresponding diode will be conducting, thus applying a voltage on the resistor and charging the
’Out’ wire.// Though the DL family is simple, its disadvantages are the lack of amplifying stages,
the lack of inverting gates (can only implement AND &. OR gates), cascading voltage ranges are
changed from the original, forward voltage drop (weak ’1’ &. ’0’) and source resistance that along
with the resistor create a voltage divider that worsens the voltage levels.
Figure 2.1: Diode logic OR gate.
Resistor-Transistor Logic
The RTL family is the first to use transistors in a digital IC. It is the simplest way we can
implement inverted gates, notably by using a minimal number of transistors.
We implement a RTL inverter in figure 2.2. When the input voltage is zero volts there is no
forward bias to the emitter-base junction, and the transistor does not conduct. Therefore no
current flows through the collector resistor, and the output voltage is +V volts. Hence, a logic ’0’
input results in a logic ’1’ output. When the input voltage is +V volts, the transistor’s emitter-base
junction will be forward biased, thus allowing the transistor to conduct. The Output will then
drop to logic ’0’.
Figure 2.2: RTL not logic gate.
4

11. 2.1. LOGIC FAMILIES
The same principles will apply for a NOR gate, as seen in figure 2.3. This time if any of the
input rises to ’1’ then the corresponding transistor will conduct, which will result in the output
discharging.
Figure 2.3: RTL NOR3 logic gate.
The obvious disadvantage of RTL is its high power dissipation when the transistor is switched
on (the power is dissipated mainly by the base resistors connected to logical "1" and by the
collector resistor). This requires that more current be supplied to and heat be removed from RTL
circuits [2].
Transistor-Transistor Logic
Invented in 1961, The TTL family uses transistors to implement the logic function and to amplify
the signal.
A TTL NAND gate is implemented in figure 2.4. When the two emitters of the input transistors
are connected to high voltage, then the emitter-base junction of the transistor is reverse biased,
that means the transistor is in reverse active mode. In reverse active mode, less magnitude
current flows in the opposite direction. This current reaches the base of the output transistor,
allowing it to conduct and pulling down the output voltage to zero. When any one of the input
terminal is low, the current through other branch flows out through this terminal. Now no current
reaches the base terminal of the output transistor, so output remains at high state [4].
5

12. CHAPTER 2. LITERATURE SURVEY
Figure 2.4: TTL NOR logic gate.
The limitations of the TTL family are mainly high power consumption and slow delay time.
NMOS Logic
The NMOS logic family uses only the n-type enhancement mode transistors (induced n-type
channel) in a Pull-Down Network (PDN) arrangement. This arrangement locates the transistors
between the Ground and the gate output. A resistor is placed between the supply voltage and
the output. With the right inputs, the PDN will allow the output to discharge into the Ground,
creating a current in the circuit. With other inputs, the PDN will not conduct, thus pulling up
the output towards the supply voltage.
The logic function is determined by the PDN. In figure 2.5 we can see how the PDN implements a
NOR function. When one of the inputs is a logic ’1’, the output discharges to a logic ’0’. When the
inputs are both ’0’ then the PDN is not conducting, hence the output is pulled up to a logic ’1’.
Figure 2.5: NMOS NOR logic gate.
The advantages of the NMOS logic family are its simplicity and low delay (n-type MOSFETs
are faster than p-type). However, a major drawback is in the steady state DC current (when the
output goes to Ground) causing large static power dissipation.
6

13. 2.1. LOGIC FAMILIES
The PMOS logic family is similar to NMOS, except it uses p-type transistors and places them
at the Pull-Up Network (PUN) and a resistor attached to Ground.
Pass Transistor Logic
Up until now we saw logic families with transistors connected to supply/Ground voltages at
one end. The PTL family uses transistors as switches to pass logic levels between nodes of a
circuit, without these transistors being connected to a supply voltage. This feature can reduce the
number of transistors used to implement a logic function by eliminating redundant transistors.
PTL comes extremely handy when producing complicated gates and memory cells like Multiplex-
ers, Flip-Flops and SRAM. Figure 2.6 shows a PTL Multiplexer using only two transistors. The
implementation is very simple to understand [3].
Figure 2.6: PTL MUX gate uses only two transistors
However, we notice that the NMOS transistors will pass a weak ’1’. To avoid that, we use a
transmission gate as seen in figure 2.7. The PMOS transistor passes a strong ’1’ and the NMOS
transistor passes a strong ’0’.
Figure 2.7: Transmission gate
7

14. CHAPTER 2. LITERATURE SURVEY
Complimentary MOS Logic
The CMOS family is a combination between the NMOS and PMOS families. The PDN consists of
n-type transistors and the PUN consists of p-type transistors. In that case, both the PDN and the
PUN have to implement the logic function.
Figure 2.8 shows the design of a NAND and NOR logic gates. We can see the relation between
the PDN and the PUN in a given CMOS gate. If the PDN has a parallel formation then the PUN
has a serial formation, and vise-versa.
Figure 2.8: CMOS NAND and NOR logic gates.
The CMOS design has managed to achieve great improvements in numerous parameters,
reaching characteristics of almost an ideal logic family. [1]
First, the static power dissipation decreases dramatically. Unlike the NMOS/PMOS logic
families, there will never be a straight path between the supply voltage and the Ground. This is a
result of the relation between the PDN and the PUN which are always complimentary, meaning
that when one is conducting the other is not. The static power dissipation is caused only by
leakage currents. These currents are more significant as the device is scaled.
Secondly, the propagation delay is rather short for both networks, though the NMOS is faster
than PMOS. In order to make both networks equal in respect to propagation delay time we use
wider p-type transistors in the PUN. The ratio between the widths of the n-type and the p-type
transistors is represented by "Œ ≤". The Œ ≤ parameter depends on the technology we are using.
Third, the rise and fall times are controlled by the sizing of the transistors. Last is the noise
margin. Ideally we want a noise margin of 50%. the supply voltage. The CMOS noise margin is
reaching values close to the ideal.
8

15. CHAPTER
3
DESIGN AND SIMULATION
T
he main objective of this chapter is to introduce a new logic family (DCMPL) that can
reduce the energy consumption while maintaining (and in some cases even improving)
the desired high performance. In this chapter we will also discuss the parameters that
are necessary to measure in order to determine the qualities of a digital gate. We will explain in
detail the different simulations used in order to correctly measure each of these parameters.
3.1 Design
in the beginning we aim to characterize the "DCMPL" design for NOR gate compared to "CMOS"
logic Nor gate. The design must sustain the golden rules:
• Any gate must provide the same logic table as the "CMOS" gate.
• Targeting high performance with minimal power consumption.
• Use smaller sizing -> less area (not must).
• Use less transistors compared to "CMOS" (optional).
• Have a differential gate (optional).
9

16. CHAPTER 3. DESIGN AND SIMULATION
3.1.1 NOR Digital Logic Gate
The CMOS NOR logic gate has a few characteristics which make it vulnerable when integrated
with an especially high fan in. The sizing rule of CMOS makes the stacking of PMOS transistors
to be an acute problem for the dynamic power consumption and the area in the physical layout.
Figure 3.1 illustrates the stacking of multiple PMOS transistors. It is evident that the high fan-in
is prone to be problematic. Table 3.2 counts the advantages and disadvantages of the classic
CMOS design for the NOR4 digital logic gate.
Figure 3.1: CMOS NOR4 gate.
Pros Cons
Small static currents High power consumption
Very robust under Process Variations Large capacitance
Well explored Large area
Table 3.1: NOR digital gate characteristic
The main idea behind the design of the DCMPL logic family is to eliminate the stacking of PMOS
transistors in the CMOS logic family design, while maintaining it’s advantages. The idea of
combining CMOS with Pass transistor logic (PTL) was originally seen as the solution, however
the final design of the DCMPL digital gate avoids using PTL. In order to better understand how
the DCMPL digital gate came to be, we offer a review of the evolution it went through in the
course of our project.
10

17. 3.1. DESIGN
First Edition
The first design offered is seen in figure 3.2. The stack of PMOS transistors is replaced with a
single one. If any of the entry bits (’A’, ’B’, ’C’ or ’D’) is a logic ’1’ then the output will discharge to
ground - a logic ’0’ - and the gate of the single PMOS transistor will be a logic ’1’. However, when
all entry bits are logic ’0’ then the gate bit of the single PMOS transistor will discharge to a logic
’0’.Notice that the gate bit of this single PMOS transistor is always complimentary to the output
bit. Thus, we named it OUTnot . The OUTnot bit is determined by the negated input bits, which
can pass either the VDD supply voltage or the voltage of the bit ’A’. In order to pass a strong ’0’
and ’1’ we use multiple transmission gates with minimal sizing. The use of PTL for the bit ’A’
saves us one transmission gate in the stack.
We tested the first edition design of Nor4. From one hand we get little improvement in the
average energy compared to "CMOS" because we use minimal sizing for PMOS. On the other
hand the worst case tpd in our design was higher. This is because loading the OUTnot to VDD
makes us pass a stack of PMOS transistors, and the capacitance of node ’A’ was the sum of two
diffusion capacitors and one gate capacitor.
Figure 3.2: First edition of DCMPL NOR4 gate.
11

18. CHAPTER 3. DESIGN AND SIMULATION
Second Edition
The next stage of the design was to convert the stack of PMOS transistors in the transmis-
sion gates stack into a PMOS transistor with an Anot gate input in parallel with the PMOS
transistors, as seen in figure 3.3. This will keep the correct truth table, while reducing the
capacitance of node A compared to the gate capacitance of the Anot transistor. As a result the
power consumption decreases. Even though for one component the Edynamic, Esc , and tpd get
better compared to the first edition it was still difficult cascading the NOR gate for a few reasons:
1. It is impossible to characterize the capacitance of a diffusion input for a library cell.
2. The design limit cascading out/(out) ÃÖ to diffusion inputs (node A) because it will be hard
to drive the capacitance of the next stage (timing rule), which can cause additional sizing
and can change the logic status of the next stage.
Figure 3.3: Second edition of DCMPL NOR4 gate.
Final Edition
To face the cascading problem we replaced the diffusion input into a gate input by using the
Differential quality of the DCMPL digital gate as an advantage (input Anot ). It helps us to
characterize the total capacitance of the cell, and improve the performance compared to the
second edition in high fan-in designs. In addition, the golden rule of beta = 2 is not obligatory in
our logic family. It means we can size our design minimally in order to reduce the area and the
capacitance on the wafer as long as our design achieves the main goals that we mention earlier.
As highlighted in the figure 3.5 below design is composed of two levels:
1. The first level (yellow) is a CMOS OR gate using minimal sizing for better power consump-
tion.
12

19. 3.1. DESIGN
2. The second level (green) is similar to a CMOS NOR gate which help us achieve a high
performance.
Figure 3.4: Last edition of DCMPL NOR4 gate.
13

20. CHAPTER 3. DESIGN AND SIMULATION
We notice a very important quality this design holds. In addition to the implementation of the
boolean functions NOR &. OR, This digital gate can also implement the functions AND &. NAND.
This is achieved by negating all the inputs of the gate.
Figure 3.5: NOR gate design with different fan in inputs.
Table 3.2: Characteristic table design
CMOS FIRST EDITION SECOND EDITION LAST EDITION
No of transistor N 2N-2 1.5N 1.5N+1
Power Equal Less Less
Tpd Equal Less Less
Sizing More Less Less
Differential
Note: The results of each edition are compared to the CMOS results.
14

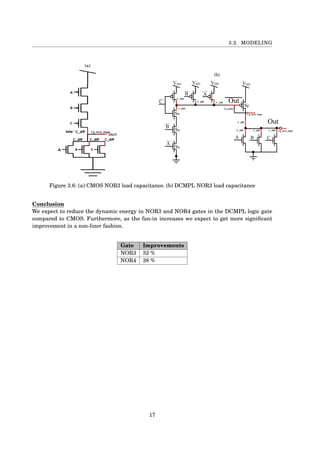
21. 3.2. MODELING
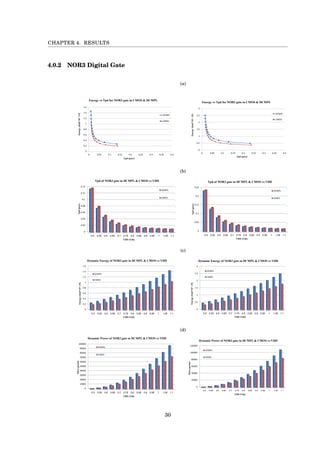
3.2 Modeling
In this chapter we aim to develop a mathematical model that anticipates the tpd and Energy of
the DCMPL logic gate for any given gate capacitance.
Power Consumption
Power Consumption of any circuit is divided into the following categories:
• Dynamic power ∼ Cload · vdd2
• static power ∼ Istatic · vdd
• short circuit power ∼ Tsc · Ipeek · vdd · f
We modeled the load capacitance which is critical for predicting the dynamic power when charging
the output of the gate. We ignore the voltage supply effect because the simulation uses each time
the same VDD . In order to find Cload we have to find all capacitance which connect directly to
wire OUT and OUTnot in both design.
In the CMOS design figure [a] the ’OUT’ wire connect to three Cdif f of the NMOS transistors,
one Cdif f of the PMOS transistor multiply by β, and the capacitance gate of the next stage.
In the DCMPL design figure [b] the ’OUT’ wire connect to three Cdif f of the NMOS transistors,
one Cdif f of the PMOS transistor, and the capacitance gate of the next stage.
more over the OUTnot wire connect to three Cdif f of the PMOS transistors, one Cdif f of the
NMOS transistor, and the capacitance gate of INPUTnot of the next stage.
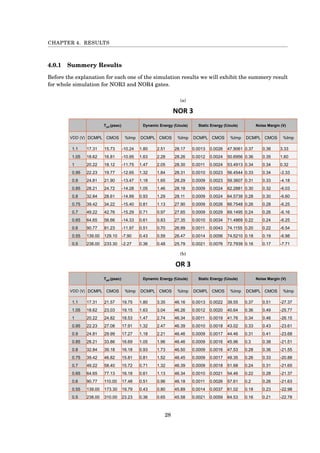
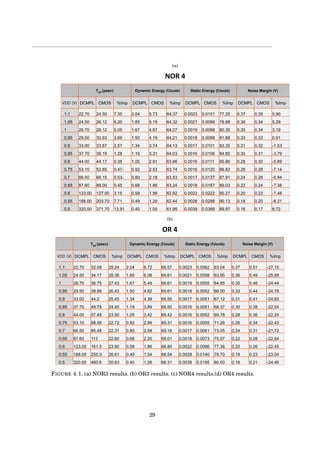
CMOS MODEL:
NOR3
N-number of inputs.
β-sizing of the pull up transistors in CMOS.
CgA|B|C = β·C +C = 4.9C.
Cout = β·CPdif f + N ·CNdif f +Cnexts tage =
3.9·CPdif f +3·CNdif f +CPgate +CNgate =
3.9C +3C +3.9C + c = 11.8C
NOR4
N-number of inputs.
β-sizing of the pull up transistors in CMOS.
CgA|B|C = β·C +C = 6.2C.
Cout = β·CPdif f + N ·CNdif f +Cnexts tage =
5.2·CPdif f +4·CNdif f +CPgate +CNgate =
5.2C +3C +5.2C + c = 14.4C
15

22. CHAPTER 3. DESIGN AND SIMULATION
DCMPL MODEL
NOR3
N-number of inputs.
β-sizing of the pull up transistors in DCMPL-minimal sizing.
CgA|B|C = C.
CgAnot|Bnot|Cnot = CNgate +CPgate = 2C.
Cout = CPdif f + N ·CNdif f +Cnexts tage =
CPdif f +3·CNdif f +CNgate =
C +3C +C = 5C.
Coutn ot = N ·CPdif f +CNdif f +CPgate +Cnexts tage =
3·CPdif f +CNdif f +CPgate +CPgate +CNgate =
3C +C +C +2C +C = 8C
NOR4
N-number of inputs.
β-sizing of the pull up transistors in DCMPL-minimal sizing.
CgA|B|C = C.
CgAnot|Bnot|Cnot = CNgate +CPgate = 2C.
Cout = CPdif f + N ·CNdif f +Cnexts tage =
CPdif f +4·CNdif f +CNgate =
C +4C +C = 6C.
Coutn ot = N ·CPdif f +CNdif f +CPgate +Cnexts tage =
4·CPdif f +CNdif f +CPgate +CPgate +CNgate =
4C +C +C +2C +C = 9C
16

23. 3.2. MODELING
(a)
(b)
VDD
Out
Out
A B
VDD
C
C
B
VDDVDD
B A
Sn
Sn
Sp
A
Sn
C_diff
C_diff
C_diff C_diff
Cg_pmos
Cg_next_stage
C_diff C_diff C_diff Cg_next_stage
C_diff
Figure 3.6: (a) CMOS NOR3 load capacitance. (b) DCMPL NOR3 load capacitance
Conclusion
We expect to reduce the dynamic energy in NOR3 and NOR4 gates in the DCMPL logic gate
compared to CMOS. Furthermore, as the fan-in increases we expect to get more significant
improvement in a non-liner fashion.
Gate Improvements
NOR3 32 %
NOR4 38 %
17

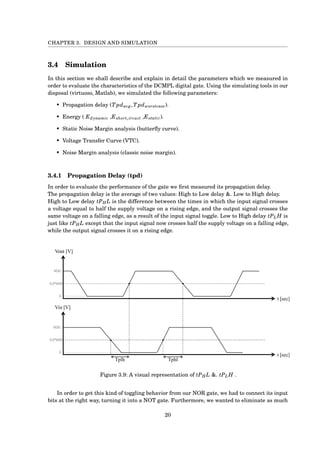
24. CHAPTER 3. DESIGN AND SIMULATION
Tpd - Elmore Delay
We use the Elmore-Delay in order to model the delay of the gate through the worst case vector by
charging and discharging the output.
In each one of the design we find the total capacitance and resistance go through transistors from
input to output.
At last we modeled how the trend line of tpd vs VDD should look like.
First we find who is the longest vector[fig3.7]. The vector who has to pass more capacitance on
the way is tplh(out) form input A.
Second we use Elmore-Delay model find how many capacitance and resistance on the critical
path so the general equation for unknown β and inputs is:
Third we know from VLSI course (assuming Cdif f const) that:
We subtitute R,C,S,β in the equation above and find that: tpd graph ∼ const· 1
V dd
In Summery we expect the tpd vs VDD will act like 1
x graph.
Figure 3.7: Charging OUT to VDD by different inputs in Nor4 gate
18

25. 3.3. LAYOUT
3.3 Layout
The layout stage is where we simulate the physical layers of our digital gate.
This is an importent stage since all the properties of our gate derive from it.
Due to the secrecy of the 28 nm proecess we can not show any photos of our layout, however we
will discuss some principles and challenges we encountered during the project as can be seen in
figure 3.8.
The first challenge was the limitation on breaking the polysilicon. furthermore the gap between
polysilicon layers must be constnt [1].
Secondly, minimizing the distance between diffusion layer is limited due to several design rules[2].
third, metal thickness often needs to increase significantly[3].
Figure 3.8: Layout Challenges in 28 nm
19

26. CHAPTER 3. DESIGN AND SIMULATION
3.4 Simulation
In this section we shall describe and explain in detail the parameters which we measured in
order to evaluate the characteristics of the DCMPL digital gate. Using the simulating tools in our
disposal (virtuoso, Matlab), we simulated the following parameters:
• Propagation delay (T pdavg,T pdworstcase).
• Energy ( Edynamic ,Eshortc ircuit ,Estatic).
• Static Noise Margin analysis (butterfly curve).
• Voltage Transfer Curve (VTC).
• Noise Margin analysis (classic noise margin).
3.4.1 Propagation Delay (tpd)
In order to evaluate the performance of the gate we first measured its propagation delay.
The propagation delay is the average of two values: High to Low delay &. Low to High delay.
High to Low delay tPHL is the difference between the times in which the input signal crosses
a voltage equal to half the supply voltage on a rising edge, and the output signal crosses the
same voltage on a falling edge, as a result of the input signal toggle. Low to High delay tPLH is
just like tPHL except that the input signal now crosses half the supply voltage on a falling edge,
while the output signal crosses it on a rising edge.
Figure 3.9: A visual representation of tPHL &. tPLH .
In order to get this kind of toggling behavior from our NOR gate, we had to connect its input
bits at the right way, turning it into a NOT gate. Furthermore, we wanted to eliminate as much
20

27. 3.4. SIMULATION
as possible the effects of an ideal input. In order to achieve that we built a chain of six NOR gates
in the following manner:
Figure 3.10: A chain of six NOR2 gates connected through input ’A’.
The ideal input is only at the first gate. The propagation delay was measured on the fifth
gate, letting the signal smoother out through the chain and letting the output drive a real load.
Notice that the input B is always grounded and Bnot is always connected to VDD . This creates
the NOT gate in relation to input A and output OUT (and being a differential gate means the
same also for Anot and OUTnot ).
We created another chain where the signal is propagating through inputs B and Bnot (thus A
is grounded and Anot is connected to VDD ). This allowed us to compare the tpd of each and every
rout through the NOR gate. Ever larger NOR gates meant we had to build more chains. So for a
NOR3 gate we had three chains, and we received three different propagation delay values: tpd
1 for input A, tpd 2 for input B and tpd 3 for input C. Averaging the three values gives us the
Average tpd . The maximal value gives us the Worst-case tpd .
3.4.2 Dynamic &. Static Energy
We measured the energy of the gate using our chains from the tpd measurement. This time we
closed the chain inside a black box and measured its power consumption using the expression
"getData("instance:pwr")" (i.e. "getPower") in the virtuoso.
Figure 3.11: The chain from the previous example is now a unified instance.
The "getPower" function returns a waveform of the power consumed by the instance at every
given time. Predictably, the power consumption is larger when the instance input gets toggled.
This creates peaks around the times where a toggle has occurred, and in between those peaks we
see a plateau. Because the input is cyclic, the ’getPower’ graph will be cyclic as well. It will consist
of two different peaks (one represents the charging of the output wire and the other represents
21

28. CHAPTER 3. DESIGN AND SIMULATION
discharge) that will be repeated in a cyclic manner.
Figure 3.12: A typical waveform returned by the ’getPower’ function. In reality the peaks are
much more narrow.
We wanted to have a constant and unified way of measuring the dynamic and static energy out
of the ’getPower’ graph. Because the energy is the integral of the power along a certain interval
we needed to properly define this interval so it will be suited for each and every measurement.
The first things we needed to define are the boundaries of the peaks in the graph. Though it
doesn’t always seem like it, when zooming in on the graph it is relatively hard to determine when
the peak has ended and plateau has started. So we defined the width of the peak as the difference
between two points: the first point is the time when the power crosses the value of 0.5 % of the
maximum height of the peak at a rising edge, and the second point is when the power crosses the
value of 0.5% of the maximum height of the peak at a falling edge. Of course this required us to
measure the maximum values of the high and low peak.
22

29. 3.4. SIMULATION
Figure 3.13: A zoomed in view of the ’getPower’ peak.
Sizing
In order to determine the sizing of the transistors in the DCMPL gates, we had to set the
standards to which the gate should live up to by comparing it to the matching CMOS gate. We
decided to size the DCMPL so that its Tpd is lower than the matching CMOS gate. However, in
some cases this means we should use relatively large transistors that consume a lot of energy and
use a lot of space. For example in the DCMPL NAND gates we have a stack of PMOS transistors,
which means that in order to achieve a low Tpd we had to increase the sizing in a way that makes
the gate inferior to its matching CMOS gate. In this case we compromised the Tpd (letting it be
slightly larger than the matching CMOS Tpd) and let the sizing be minimal.
23

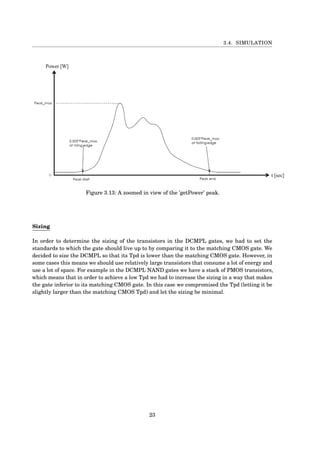
30. CHAPTER 3. DESIGN AND SIMULATION
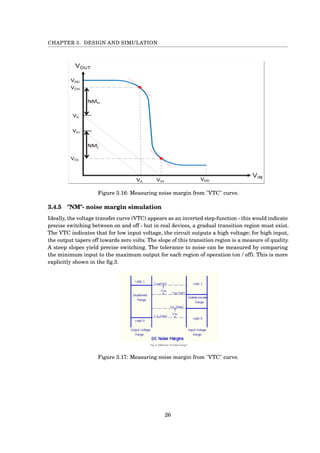
3.4.3 "SNM"- Static Noise Margin
The "SNM" analysis is taken from volatile memory cells such as SRAM memory.
We connected two gates as a ring oscillator of two inverters and checked what is the maximum
noise we can add to the input while still keeping a stable data in the cell.
In order to measure the SNM we used transformation circuits to rotate the VTC graph by 45◦
.
Then we ran a DC sweep from -VDD /sqrt(2) to VDD /sqrt(2) on V uaxis and found what is the
maximum diagonal of the square in the right and left side.
And finely, the minimum of the two diagonals will give us the "SNM" measurement.
(a) (b) (c)
(d) (e)
(f)
FIGURE 3.14. (a) A Ring oscillator configuration help to indicate what is max limit of
noise keep the system stable. Figure reproduced from [? ]. (b) Design of the first
transformation function that flip "Y" axis by 45◦
. Figure reproduced from [? ]. (c)
Design of the second transformation function that flip "X" axis by 45◦
.(d) The ideal
of the"snm" simulation is to find the max square in the overlapping area between
two original "VTC" curves.Figure reproduced from [? ]. (e) After we process two
max square from tow different overlapping area we compare between them and
take the minimal square for worst case scenario.Figure reproduced from [? ]. (f)
Summarizing all steps to find static noise margin in any system
24

31. 3.4. SIMULATION
The main challenge was to take any gate in our library and make it work as differential inverter
with 2 inputs/outputs. For example we took Nor2 in "DCMPL" and shorted all the regular inputs
together and all input not together. By doing that we force the gate to act as a differential inverter
with two inputs and two outputs:
Figure 3.15: Transform Nor2 gate to inverter with 2 inputs in ring oscillator configuration.
Unfortunately the VTC of "DCMPL" family diverts from the classic butterfly curve of the
CMOS. Because of the illogical results we decided to use the classic VTC simulation in order to
compare the NM between CMOS and DCMPL family logic.
3.4.4 "VTC"- voltage transfer curve simulation
Digital inverter quality is often measured using the Voltage Transfer Curve (VTC), which is a
plot of input vs. output voltage. From such a graph, device parameters including noise tolerance,
gain, and operating logic-levels can be obtained.
25

32. CHAPTER 3. DESIGN AND SIMULATION
Figure 3.16: Measuring noise margin from "VTC" curve.
3.4.5 "NM"- noise margin simulation
Ideally, the voltage transfer curve (VTC) appears as an inverted step-function - this would indicate
precise switching between on and off - but in real devices, a gradual transition region must exist.
The VTC indicates that for low input voltage, the circuit outputs a high voltage; for high input,
the output tapers off towards zero volts. The slope of this transition region is a measure of quality.
A steep slopes yield precise switching. The tolerance to noise can be measured by comparing
the minimum input to the maximum output for each region of operation (on / off). This is more
explicitly shown in the fig.3.
Figure 3.17: Measuring noise margin from "VTC" curve.
26

33. CHAPTER
4
RESULTS
I
n this chapter we present the data resulted from the simulations mentioned earlier. We also
present the data in ways that can help us as engineers understand the system in the optimal
manner. notice that in some of the results we distinguish between pre-layout &. post-layout
results, as well as between NOR &. OR digital gates.
27

34. CHAPTER 4. RESULTS
4.0.1 Summery Results
Before the explanation for each one of the simulation results we will exhibit the summery result
for whole simulation for NOR3 and NOR4 gates.
(a)
Noise Margin (V)Static Energy (fJoule)Dynamic Energy (fJoule)Tpd (psec)
%ImpCMOSDCMPL%ImpCMOSDCMPL%ImpCMOSDCMPL%ImpCMOSDCMPLVDD (V)
3.330.360.3747.90610.00260.001328.172.511.80-10.2415.7317.311.1
1.600.350.3650.69560.00240.001228.262.281.63-10.9516.8118.621.05
0.320.340.3453.49130.00240.001128.302.051.47-11.7518.1220.221
2.33-0.340.3356.45440.00230.001028.311.841.32-12.6519.7722.230.95
4.18-0.330.3159.36070.00230.000928.291.651.18-13.4721.9024.810.9
6.03-0.320.3062.28810.00240.000928.181.461.05-14.2824.7228.210.85
6.60-0.300.2864.57390.00240.000928.111.290.93-14.9928.6132.840.8
6.25-0.280.2666.75480.00260.000927.901.130.81-15.4034.2239.420.75
6.16-0.260.2469.14950.00290.000927.650.970.71-15.2942.7649.220.7
6.25-0.240.2271.48690.00340.001027.350.830.61-14.3356.6664.650.65
6.54-0.220.2074.11550.00430.001126.990.700.51-11.9781.2390.770.6
6.98-0.190.1874.52100.00560.001426.470.590.43-7.90129.10139.000.55
7.71-0.170.1672.79390.00760.002125.790.480.36-2.27233.30238.000.5
NOR 3
(b)
Noise Margin (V)Static Energy (fJoule)Dynamic Energy (fJoule)Tpd (psec)
%ImpCMOSDCMPL%ImpCMOSDCMPL%ImpCMOSDCMPL%ImpCMOSDCMPLVDD (V)
-27.370.510.3739.550.00220.001346.163.351.8019.7521.5717.311.1
-25.770.490.3640.640.00200.001246.263.041.6319.1523.0318.621.05
-26.150.460.3441.760.00190.001146.342.741.4718.5324.8220.221
-23.610.430.3343.020.00180.001046.392.471.3217.9127.0822.230.95
-23.680.410.3144.460.00170.000946.462.211.1817.2729.9924.810.9
-21.510.380.345.960.00160.000946.461.961.0516.6933.8628.210.85
-21.550.360.2847.530.00160.000946.501.730.9316.1839.1832.840.8
-20.880.330.2649.350.00170.000946.451.520.8115.8146.8239.420.75
-21.650.310.2451.680.00180.000946.391.320.7115.7258.4049.220.7
-21.370.280.2254.460.00210.001046.341.130.6116.1877.1364.650.65
-21.630.260.257.610.00260.001146.180.960.5117.48110.0090.770.6
-22.980.230.1861.020.00370.001445.890.800.4319.79173.30139.000.55
-22.780.210.1664.530.00590.002145.580.650.3623.23310.00238.000.5
OR 3
28

35. (a)
Noise Margin (V)Static Energy (fJoule)Dynamic Energy (fJoule)Tpd (psec)
%ImpCMOSDCMPL%ImpCMOSDCMPL%ImpCMOSDCMPL%ImpCMOSDCMPLVDD (V)
5.900.350.3777.350.01010.002364.375.732.047.3524.5022.701.1
5.290.340.3678.880.00990.002164.325.191.856.2026.1224.501.05
3.190.340.3580.350.00980.001964.274.671.675.0528.1226.701
0.910.330.3381.880.00980.001864.214.191.503.6930.6329.500.95
1.53-0.320.3183.350.01010.001764.133.741.342.5733.8733.000.9
3.79-0.310.3084.800.01060.001664.033.311.191.2838.1937.700.85
5.89-0.300.2885.860.01110.001663.862.911.050.3844.1744.000.8
7.14-0.280.2686.820.01200.001663.742.530.92-0.4752.8553.100.75
6.94-0.260.2487.910.01370.001763.532.180.80-0.5366.1566.500.7
7.38-0.240.2289.030.01670.001863.241.860.680.4588.0087.600.65
7.48-0.220.2090.270.02220.002262.921.560.583.15127.00123.000.6
8.31-0.200.1890.130.02880.002862.441.290.497.71203.70188.000.55
8.720.170.1689.970.03890.003961.951.050.4013.91371.70320.000.5
NOR 4
(b)
Noise Margin (V)Static Energy (fJoule)Dynamic Energy (fJoule)Tpd (psec)
%ImpCMOSDCMPL%ImpCMOSDCMPL%ImpCMOSDCMPL%ImpCMOSDCMPLVDD (V)
-27.150.510.3763.040.00620.002369.576.722.0429.2432.0822.701.1
-25.990.490.3663.950.00580.002169.616.081.8528.3634.1724.501.05
-24.440.460.3564.950.00550.001969.615.491.6727.4336.7526.701
-24.780.440.3366.000.00520.001869.614.921.5026.4339.9929.500.95
-24.830.410.3167.120.00510.001769.554.391.3425.4544.233.000.9
-22.040.380.3068.370.00510.001669.503.891.1924.4549.7837.700.85
-22.240.360.2869.780.00520.001669.423.421.0523.5057.4944.000.8
-22.430.340.2671.260.00550.001669.312.990.9222.7268.5853.100.75
-21.720.310.2473.050.00610.001769.192.580.8022.3185.4866.500.7
-22.640.280.2275.070.00730.001869.012.200.6822.6011387.600.65
-22.450.260.2077.360.00960.002268.801.860.5823.90161.5123.000.6
-23.040.230.1879.700.01400.002868.541.540.4926.61255.9188.000.55
-24.460.210.1680.000.01950.003968.311.260.4030.63460.6320.000.5
OR 4
FIGURE 4.1. (a) NOR3 results. (b) OR3 results. (c) NOR4 results.(d) OR4 results.
29

36. CHAPTER 4. RESULTS
4.0.2 NOR3 Digital Gate
(a)
10‫אוקטובר‬16
1
0
0.5
1
1.5
2
2.5
3
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.05
0.1
0.15
0.2
0.25
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(b)
1
0
0.5
1
1.5
2
2.5
3
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.05
0.1
0.15
0.2
0.25
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(c)
10‫אוקטובר‬16
0
0.5
1
1.5
2
2.5
3
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
20000
40000
60000
80000
100000
120000
Pdyn(pwatt)
Dynamic Power of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
10000
20000
30000
40000
50000
60000
70000
80000
90000
100000
Pdyn(pwatt)
Dynamic Power of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(d)
10‫אוקטובר‬16
0
0.5
1
1.5
2
2.5
3
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
20000
40000
60000
80000
100000
120000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynamic Power of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
100000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynamic Power of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
30

37. (a)
‫ח‬'/‫תשרי‬/‫תשע‬"‫ז‬
1
0
0.0005
0.001
0.0015
0.002
0.0025
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.0002
0.0004
0.0006
0.0008
0.001
0.0012
0.0014
0.0016
0.0018
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of NOR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
FIGURE 4.2. Left column: PRE LAYOUT, Right column: POST LAYOUT (a) The graph
places the worst case tpd and it’s matching dynamic energy point for each VDD
between 0.5-1.1 volts with 0.05v steps. (b) The worst case tpd For each VDD between
0.5-1.1 volts with 0.05v steps. (c) The worst case dynamic energy for each VDD
between 0.5-1.1 volts with 0.05v steps.(d) The worst case dynamic Power for each
VDD between 0.5-1.1 volts with 0.05v steps. (e) The worst case Static Power for
each VDD between 0.5-1.1 volts with 0.05v steps.
31

38. CHAPTER 4. RESULTS
4.0.3 NOR4 Digital Gate
(a)
19‫אוקטובר‬16
1
0
1
2
3
4
5
6
7
0 50 100 150 200 250 300 350 400
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
0 50 100 150 200 250
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
50
100
150
200
250
300
350
400
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
50
100
150
200
250
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
1
2
3
4
5
6
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(b)
19‫אוקטובר‬16
1
0
1
2
3
4
5
6
7
0 50 100 150 200 250 300 350 400
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
0 50 100 150 200 250
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
50
100
150
200
250
300
350
400
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
50
100
150
200
250
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
1
2
3
4
5
6
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(c)
19‫אוקטובר‬16
1
0
1
2
3
4
5
6
7
0 50 100 150 200 250 300 350 400
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
0 50 100 150 200 250
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for NOR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
50
100
150
200
250
300
350
400
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
50
100
150
200
250
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
1
2
3
4
5
6
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(d)
19‫אוקטובר‬16
0
20000
40000
60000
80000
100000
120000
140000
160000
180000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynamic Power of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
20000
40000
60000
80000
100000
120000
140000
160000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynramic Power of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
32

39. (a)
1
0
0.005
0.01
0.015
0.02
0.025
0.03
1.11.0510.950.90.850.80.750.70.650.60.55
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
1.11.0510.950.90.850.80.750.70.650.60.55
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of NOR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
FIGURE 4.3. Left column: PRE LAYOUT, Right column: POST LAYOUT. (a) The graph
places the worst case tpd and it’s matching dynamic energy point for each VDD
between 0.5-1.1 volts with 0.05v steps. (b) The worst case tpd For each VDD between
0.5-1.1 volts with 0.05v steps. (c) The worst case dynamic energy for each VDD
between 0.5-1.1 volts with 0.05v steps.(d) The worst case dynamic Power for each
VDD between 0.5-1.1 volts with 0.05v steps. (e) The worst case Static Power for
each VDD between 0.5-1.1 volts with 0.05v steps
33

40. CHAPTER 4. RESULTS
4.0.4 OR3 Digital Gate
(a)
‫ח‬'/‫תשרי‬/‫תשע‬"‫ז‬
1
0
0.5
1
1.5
2
2.5
3
3.5
4
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
4
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR3 gate in CMOS & DCMPL
DCMPL
CMOS
0.25 0.3 0.35 0.4
sec)
e in CMOS & DCMPL
DCMPL
CMOS
1.11.0510.950.90.850.8
olt)
L & CMOS vs VDD
DCMPL
CMOS
1.11.0510.950.90.850.8
Volt)
DCMPL & CMOS vs VDD
0
20000
40000
60000
80000
100000
120000
140000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynamic Power of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.001
0.002
0.003
0.004
0.005
0.006
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(b)
‫ח‬'/‫תשרי‬/‫תשע‬"‫ז‬
1
0
0.5
1
1.5
2
2.5
3
3.5
4
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
4
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR3 gate in CMOS & DCMPL
DCMPL
CMOS
0.25 0.3 0.35 0.4
sec)
e in CMOS & DCMPL
DCMPL
CMOS
1.11.0510.950.90.850.8
olt)
L & CMOS vs VDD
DCMPL
CMOS
1.11.0510.950.90.850.8
Volt)
DCMPL & CMOS vs VDD
0
20000
40000
60000
80000
100000
120000
140000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynamic Power of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.001
0.002
0.003
0.004
0.005
0.006
1.11.0510.950.90.850.80.750.70.650.60.550.5Energy(Joul*10^-15)
VDD (Volt)
Static Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(c)
‫ח‬'/‫תשרי‬/‫תשע‬"‫ז‬
1
0
0.5
1
1.5
2
2.5
3
3.5
4
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
4
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR3 gate in CMOS & DCMPL
DCMPL
CMOS
0.25 0.3 0.35 0.4
sec)
e in CMOS & DCMPL
DCMPL
CMOS
1.11.0510.950.90.850.8
olt)
L & CMOS vs VDD
DCMPL
CMOS
1.11.0510.950.90.850.8
Volt)
DCMPL & CMOS vs VDD
0
20000
40000
60000
80000
100000
120000
140000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynamic Power of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.001
0.002
0.003
0.004
0.005
0.006
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR3 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(d)
‫ח‬'/‫תשרי‬/‫תשע‬"‫ז‬
0
20000
40000
60000
80000
100000
120000
140000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynamic Power of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
20000
40000
60000
80000
100000
120000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynamic Power of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
34

41. (a)
1
0
0.001
0.002
0.003
0.004
0.005
0.006
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.0005
0.001
0.0015
0.002
0.0025
0.003
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of OR3 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
FIGURE 4.4. Left column: PRE LAYOUT, Right column: POST LAYOUT
(a) (a) The graph places the worst case tpd and it’s matching dynamic energy point
for each VDD between 0.5-1.1 volts with 0.05v steps. (b) The worst case tpd For
each VDD between 0.5-1.1 volts with 0.05v steps. (c) The worst case dynamic energy
for each VDD between 0.5-1.1 volts with 0.05v steps.(d) The worst case dynamic
Power for each VDD between 0.5-1.1 volts with 0.05v steps. (e) The worst case
Static Power for each VDD between 0.5-1.1 volts with 0.05v steps.
35

42. CHAPTER 4. RESULTS
36

43. 4.0.5 OR4 Digital Gate
(a)
19‫אוקטובר‬16
1
0
1
2
3
4
5
6
7
8
0 100 200 300 400 500
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 50 100 150 200 250 300
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
50
100
150
200
250
300
350
400
450
500
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
50
100
150
200
250
300
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
1
2
3
4
5
6
7
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
4
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(b)
19‫אוקטובר‬16
1
0
1
2
3
4
5
6
7
8
0 100 200 300 400 500
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 50 100 150 200 250 300
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
50
100
150
200
250
300
350
400
450
500
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
50
100
150
200
250
300
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
1
2
3
4
5
6
7
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
4
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(c)
19‫אוקטובר‬16
1
0
1
2
3
4
5
6
7
8
0 100 200 300 400 500
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 50 100 150 200 250 300
Energy(Joul*10^-15)
Tpd (psec)
Energy vs Tpd for OR4 gate in CMOS & DCMPL
DCMPL
CMOS
0
50
100
150
200
250
300
350
400
450
500
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
50
100
150
200
250
300
1.11.0510.950.90.850.80.750.70.650.60.550.5
Tpd(psec)
VDD (Volt)
Tpd of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
1
2
3
4
5
6
7
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.5
1
1.5
2
2.5
3
3.5
4
1.11.0510.950.90.850.80.750.70.650.60.550.5
Energy(Joul*10^-15)
VDD (Volt)
Dynamic Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
(d)
19‫אוקטובר‬16
0
20000
40000
60000
80000
100000
120000
140000
160000
180000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynamic Power of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
20000
40000
60000
80000
100000
120000
140000
160000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
Dynramic Power of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0.012
0.014
Static Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0.005
0.006
)
Static Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
37

44. CHAPTER 4. RESULTS
(a)
1
0
20000
40000
60000
80000
100000
120000
140000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
CMOS
0
20000
40000
60000
80000
100000
120000
1.11.0510.950.90.850.80.750.70.650.60.550.5
Pdyn(pwatt)
VDD (Volt)
CMOS
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
1.11.0510.950.90.850.80.750.70.650.60.55
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
0
0.001
0.002
0.003
0.004
0.005
0.006
1.11.0510.950.90.850.80.750.70.650.60.55
Energy(Joul*10^-15)
VDD (Volt)
Static Energy of OR4 gate in DCMPL & CMOS vs VDD
DCMPL
CMOS
FIGURE 4.5. Left column: PRE LAYOUT, Right column: POST LAYOUT
(a) The graph places the worst case tpd and it’s matching dynamic energy point for
each VDD between 0.5-1.1 volts with 0.05v steps. (b) The worst case tpd For each
VDD between 0.5-1.1 volts with 0.05v steps. (c) The worst case dynamic energy
for each VDD between 0.5-1.1 volts with 0.05v steps.(d) The worst case dynamic
Power for each VDD between 0.5-1.1 volts with 0.05v steps. (e) The worst case
Static Power for each VDD between 0.5-1.1 volts with 0.05v steps.
Summery Energy vs tpd simulation
It seems from the Energy vs tpd post layout graph that:
• NOR3 and NOR4 gates improve the power consumption for any supply voltage who indicate
our Energy modelling expection.
• The Energy graph has a non-liner trend line as the fan-in increases which indicate our
model.
• The DCMPL NOR3 has larger worst case tpd (around 7 %) compare to CMOS NOR3 depand
on the vdd, as opposed to NOR4 which improve the performance compere to CMOS design.
• We fitted the tpd vs VDD graph using the MATLAB curve fit tool and found that for NOR3
and NOR4 gates the trendline can be expressed by the ratio tpd ∼ 1
V DD1.8 . This ratio
resembles the 1
V DD ratio in our model, however it is not similar.
38

45. 4.1. VTC-VOLTAGE TRANSFER CURVE
4.1 VTC-voltage transfer curve
Our Logic gates have differential inputs and outputs which oblige us to find the effect of
any input vector on any output vector.
Our logic gate has two optional sweeps:
1. Charge out to ’1’, discharge OUTnot to ’0’.
2. Discharge out to ’0’, charge OUTnot to ’1’.
At any optional sweep a different input vector causes a different effect. For example:
Charging out to VDD at the Nor4 design. There will be a difference between setting the ’B’
input from ’1’ to ’0’ and setting the ’D’ input from ’1’ to ’0’ logic. This difference based on
how many parasitic capacitance the logic gate should discharge before the OUTnot bit is
unloaded to ground.
D_NOT
C_NOT B_NOT A_NOT
B
C D
OUT
C_NOT
B_NOT
A
OUT_NOT
A_NOT
D_NOT
C_NOT B_NOT A_NOT
B C D
OUT
C_NOT
B_NOT
A
OUT_NOT
A_NOT
VDD
GND
CAPACITANCE
Figure 4.6: Charging OUT to VDD by different inputs in Nor4 gate
Expectation
As we can see in the figure 4.7, discharging the OUT bit to Ground requires passing
only one NMOS transistor compared to discharging OUTnot to ground which requires
passing four NMOS transistors. Therefore we expect to get a sharper ’VTC’ graph when
discharging the output bit to Ground by passing through the transistors controlled by
non-negated inputs in the second level of the gate, compared to transistors with negated
input from the first level of the gate.
Note
We decided to title all the graphs by the toggling of the OUT bit, but it is obvious that
if we charge out to ’1’ - similarly OUTnot discharges to ’0’. The toggle in the OUT bit is
represented in the graph by ’INPUT’ vector and the toggle in OUTnot is represented in the
graph by INPUTnot vector.
39

46. CHAPTER 4. RESULTS
4.1.1 CLASIC SIMULATION
23‫אוקטובר‬16
1
Figure 4.7: The VTC graph above show the different between regular input and INPUTnot
compare to CMOS.
40

47. 4.1. VTC-VOLTAGE TRANSFER CURVE
4.1.2 MONTE CARLO SIMULATION
(a) (b)
(c) (d)
FIGURE 4.8. Left column: PRE LAYOUT, Right column: POST LAYOUT
(a) A comparison between the voltage offsets of DCMPL and CMOS NOR3
with VDD of 0.9 volts in pre-layout simulation. (b) A comparison between the
voltage offsets of DCMPL and CMOS NOR3 with VDD of 0.9 volts in post-layout
simulation. (c) A comparison between the voltage offsets of DCMPL and CMOS
NOR3 with VDD of 0.5 volts in pre-layout simulation.(d) A comparison between the
voltage offsets of DCMPL and CMOS NOR3 with VDD of 0.5 volts in post-layout
simulation..
41

48. CHAPTER 4. RESULTS
4.2 Noise Margin
(a)
(b)
FIGURE 4.9. Left column: PRE LAYOUT, Right column: POST LAYOUT
(a) A comparison between the noise margin values of DCMPL and CMOS NOR3
digital gates. (b) A comparison between the noise margin values of DCMPL and
CMOS NOR4 digital gates.
42

49. CHAPTER
5
SUMMARY & CONCLUSIONS
I
n this project we introduced a new CMOS based digital logic family at 28nm process
technology which aims to reduce the NOR digital gate's energy consumption while
maintaining the high performance quality desired in today's technological devices. We
focused on bringing a sophisticated new design to the CMOS NOR digital gate which will
reduce the issues of large PMOS transistors sizing. This design, named DCMPL, has gone
through the strictest simulation tests in order to prevail as the suitable design to achieve
our goals. As a consequence, The validation of the DCMPL's design occupied the lion share
of our work.
The 28nm DCMPL digital gate has demonstrated to be capable of achieving significant
improvements in various factors compared to CMOS. The static energy dissipation is much
lower than at the CMOS gates, making it extremely useful in portable battery based and
IOT devices. Moreover, the dynamic energy dissipation had decreased thanks to the low
capacitance of the minimized transistors. Other factors, such as propagation delay and
noise-margin, are either similar or with proximity to CMOS. However, In the case of OR
digital gate, we receive a notable decrease in the DCMPL propagation delay compared to
CMOS due to the differential property. Furthermore, The Monte-Carlo analysis shows the
DCMPL isn't particularly sensitive to process variations.
The unique design of the DCMPL digital gate allows us to produce 28nm logic circuits with
a single layout cell, reducing the area on chip especially when high fan-in gates are at place,
while saving energy and maintaining the high performance needed for today's devices. The
DCMPL digital gate can be efficient when integrated in large modules such as encoders,
Mux, tag comparators, etc. In summary, as technology advances VLSI industries will have
to innovate and adjust their designs in order to keep up with the growing demand for ever
more low energy high performance systems. We believe that the 28nm DCMPL digital gate
can take part in the future of that industry.
In order to optimize the 28nm process DCMPL digital gate Future research may focus on
the issue of High-K metal gate and its influence on electron-hole mobility in the conductance
channel. Better understanding of this issue can lead to progress in pinpointing the gate's β
coefficient. Moreover, additional modeling and characterization is required for establishing
43

50. CHAPTER 5. SUMMARY & CONCLUSIONS
a full model library.
44

51. BIBLIOGRAPHY
[1] R. J. BAKER, CMOS: circuit design, layout, and simulation (Second ed.), Wiley-IEEE,
2008.
[2] IBM, Transistor Component Circuits, IBM.
[3] C. F. H. JAUME SEGURA, CMOS electronics: how it works, how it fails, Wiley-IEEE,
2004.
[4] W. R. B. JR., MECL System Design Handbook 2nd ed., Motorola Semiconductor Prod-
ucts Inc. vi., 1972.
[5] B. SYKES, Why test bonds?, Global SMT & Packaging magazine, (2010).
45