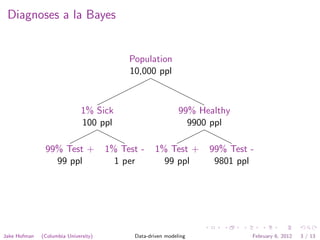
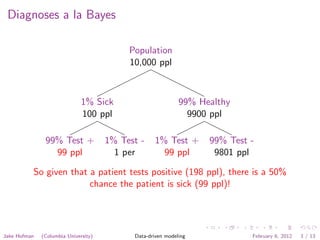
The document discusses using Naive Bayes classifiers for document classification. It explains how to represent documents as word vectors and model each word as an independent Bernoulli random variable. The likelihood of a document belonging to a class is calculated, and Bayes' rule is used to determine the posterior probability. Parameters are estimated by counting words in documents of each class. Weights and bias terms are calculated to yield a linear classifier, and predictions are made by adding the weights of words that appear.

1. Data-driven modeling
APAM E4990
Jake Hofman
Columbia University
February 6, 2012
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 1 / 13

2. Diagnoses a la Bayes1
• You’re testing for a rare disease:
• 1% of the population is infected
• You have a highly sensitive and specific test:
• 99% of sick patients test positive
• 99% of healthy patients test negative
• Given that a patient tests positive, what is probability the
patient is sick?
1
Wiggins, SciAm 2006
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 2 / 13

3. Diagnoses a la Bayes
Population
10,000 ppl
1% Sick 99% Healthy
100 ppl 9900 ppl
99% Test + 1% Test - 1% Test + 99% Test -
99 ppl 1 per 99 ppl 9801 ppl
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 3 / 13

4. Diagnoses a la Bayes
Population
10,000 ppl
1% Sick 99% Healthy
100 ppl 9900 ppl
99% Test + 1% Test - 1% Test + 99% Test -
99 ppl 1 per 99 ppl 9801 ppl
So given that a patient tests positive (198 ppl), there is a 50%
chance the patient is sick (99 ppl)!
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 3 / 13

5. Diagnoses a la Bayes
Population
10,000 ppl
1% Sick 99% Healthy
100 ppl 9900 ppl
99% Test + 1% Test - 1% Test + 99% Test -
99 ppl 1 per 99 ppl 9801 ppl
The small error rate on the large healthy population produces
many false positives.
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 3 / 13

6. Inverting conditional probabilities
Bayes’ Theorem
Equate the far right- and left-hand sides of product rule
p (y |x) p (x) = p (x, y ) = p (x|y ) p (y )
and divide to get the probability of y given x from the probability
of x given y :
p (x|y ) p (y )
p (y |x) =
p (x)
where p (x) = y ∈ΩY p (x|y ) p (y ) is the normalization constant.
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 4 / 13

7. Diagnoses a la Bayes
Given that a patient tests positive, what is probability the patient
is sick?
99/100 1/100
p (+|sick) p (sick) 99 1
p (sick|+) = = =
p (+) 198 2
99/1002 +99/1002 =198/1002
where p (+) = p (+|sick) p (sick) + p (+|healthy ) p (healthy ).
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 5 / 13

8. (Super) Naive Bayes
We can use Bayes’ rule to build a one-word spam classifier:
p (word|spam) p (spam)
p (spam|word) =
p (word)
where we estimate these probabilities with ratios of counts:
# spam docs containing word
p (word|spam) =
ˆ
# spam docs
# ham docs containing word
p (word|ham)
ˆ =
# ham docs
# spam docs
p (spam)
ˆ =
# docs
# ham docs
p (ham)
ˆ =
# docs
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 6 / 13

9. (Super) Naive Bayes
$ ./enron_naive_bayes.sh meeting
1500 spam examples
3672 ham examples
16 spam examples containing meeting
153 ham examples containing meeting
estimated P(spam) = .2900
estimated P(ham) = .7100
estimated P(meeting|spam) = .0106
estimated P(meeting|ham) = .0416
P(spam|meeting) = .0923
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 7 / 13

10. (Super) Naive Bayes
$ ./enron_naive_bayes.sh money
1500 spam examples
3672 ham examples
194 spam examples containing money
50 ham examples containing money
estimated P(spam) = .2900
estimated P(ham) = .7100
estimated P(money|spam) = .1293
estimated P(money|ham) = .0136
P(spam|money) = .7957
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 8 / 13

11. (Super) Naive Bayes
$ ./enron_naive_bayes.sh enron
1500 spam examples
3672 ham examples
0 spam examples containing enron
1478 ham examples containing enron
estimated P(spam) = .2900
estimated P(ham) = .7100
estimated P(enron|spam) = 0
estimated P(enron|ham) = .4025
P(spam|enron) = 0
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 9 / 13

12. Naive Bayes
Represent each document by a binary vector x where xj = 1 if the
j-th word appears in the document (xj = 0 otherwise).
Modeling each word as an independent Bernoulli random variable,
the probability of observing a document x of class c is:
x
p (x|c) = θjcj (1 − θjc )1−xj
j
where θjc denotes the probability that the j-th word occurs in a
document of class c.
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 10 / 13

13. Naive Bayes
Using this likelihood in Bayes’ rule and taking a logarithm, we have:
p (x|c) p (c)
log p (c|x) = log
p (x)
θjc θc
= xj log + log(1 − θjc ) + log
1 − θjc p (x)
j j
where θc is the probability of observing a document of class c.
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 11 / 13

14. Naive Bayes
We can eliminate p (x) by calculating the log-odds:
p (1|x) θj1 (1 − θj0 ) 1 − θj1 θ1
log = xj log + log + log
p (0|x) θj0 (1 − θj1 ) 1 − θj0 θ0
j j
wj
w0
which gives a linear classifier of the form w · x + w0
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 12 / 13

15. Naive Bayes
We train by counting words and documents within classes to
estimate θjc and θc :
ˆ njc
θjc =
nc
ˆ nc
θc =
n
and use these to calculate the weights wj and bias w0 :
ˆ ˆ
ˆ ˆ
θj1 (1 − θj0 )
ˆ
wj = log
ˆ ˆ
θj0 (1 − θj1 )
ˆ
1 − θj1 ˆ
θ1
w0 =
ˆ log + log .
ˆ
1 − θj0 ˆ
θ0
j
We we predict by simply adding the weights of the words that
appear in the document to the bias term.
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 13 / 13

16. Naive Bayes
In practice, this works better than one might expect given its
simplicity2
2
http://www.jstor.org/pss/1403452
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 14 / 13

17. Naive Bayes
Training is computationally cheap and scalable, and the model is
easy to update given new observations2
2
http://www.springerlink.com/content/wu3g458834583125/
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 14 / 13

18. Naive Bayes
Performance varies with document representations and
corresponding likelihood models2
2
http://ceas.cc/2006/15.pdf
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 14 / 13

19. Naive Bayes
It’s often important to smooth parameter estimates (e.g., by
adding pseudocounts) to avoid overfitting
Jake Hofman (Columbia University) Data-driven modeling February 6, 2012 14 / 13