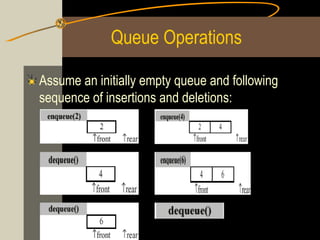
Queues are first-in, first-out data structures where elements are added to the rear of the queue and removed from the front, and can be implemented using arrays where the front and rear indices track the start and end of the queue, with circular queue implementations overcoming space limitations by treating the array as a circular buffer. Common queue operations include enqueue to add an element, dequeue to remove an element, and checks for empty and full queues.

1. Data Structures
Queues

2. Problem to be Solved
It is so often necessary to wait one’s turn before having
access to something.
We may want to simulate a real life situation of a waiting
line, like
– A line of people waiting to purchase tickets, where the first
person in line is the first person served.
With in a computer system there may be lines of tasks
– Waiting for the printer
– Waiting for access to disk storage

3. Queue
We define a queue to be a list in which
– All additions to the list are made at one end, and
– All deletions from the list are made at the other end
Queues are also called first-in, first-out lists, or FIFO
for short.
The entry in a queue ready to be served, will be
– the first entry that will be removed from the queue,
– We call this the front of the queue.

4. Queue
Insertion (enqueue) occurs at the front location of
a queue.
Deletion (dequeue) occurs at the rear location of
a queue
The general queue model is
Queue Q
Dequeue( ) Enqueue (x)

5. Queue

6. Queue Operations
The following operations are needed to properly
manage a queue.
clear() - Clear the queue.
isEmpty() – Check to see if the queue is empty.
isFull() – Check to see if the queue is full
enqueue(el) – Put the element el at the end of the
queue.
dequeue() – Take the first element from the queue.

7. Queue Operations
Assume an initially empty queue and following
sequence of insertions and deletions:

8. Queue Operations

9. Implementations of Queues
1. The Physical Model:
implement a queue by using an array.
We must keep track of both the front and the rear of the queue.
One method would be to keep the front of the queue always in the first location of
the array.
An entry could be appended to the queue simply by increasing the counter
showing the rear.
10 12 7
Delete an entry pointer by the front, but after the fist entry was served, all the
remaining entries would need to be moved one position up the queue to fill in the
vacancy, which would be an expensive process.
12 7

10. Implementations of Queues
2. Linear Implementation
In this implementation an array with two indices will be used.
One index indicates front of queue and second index indicates rear of
queue.
using front and rear indices there is no need of moving any entries.
To enqueue an entry to the queue, we simply increase the rear by one and
put the entry in that position
12 7 12 7 8
To dequeue an entry, we take it from the position at the front and then
increase the front by one.
7 8

11. Implementations of Queues
Disadvantage of Linear Implementation:
Both the front and rear indices are increased but never
decreased.therefore an unbounded amount of storage will be
needed for the queue.
Advantage of Linear Implementation:
This method is helpful in the situations where queue is
regularly emptied.
A series of requests is allowed to build up to a certain point,
and then a task is initiated that clears all the requests before
returning.
At a time when the queue is empty, the front and rear can
both be reset to the beginning of the array.

12. Implementations of Queues
3. Circular Arrays
In concept, We can overcome the disadvantage of linear implementation by
thinking of the array as a circle rather than a straight line.
As entries are added and removed from the queue, the head will continually
chase the tail around the array.
To implement a circular array as an ordinary array, we think of the positions
around the circle as numbered from 0 to MAX-1, where MAX is the total
number of entries in the array.
Moving the indices is just the same as doing modular arithmetic.
When we increase an index past MAX-1, we start over again at 0. E.g. if we
add four hours to ten o`clock, we obtain two o`clock.
7 8 9 12 7 8 9

13. Implementations of Queues
we can increase an index i by 1 in a circular array by
writing
if(i >= MAX-1)
i = 0;
else
i++;
We can also do this by using % operator i = (i+1) %
MAX;

14. Implementations of Queues
Boundary Conditions in Circular Queue:
Boundary conditions are indicators that a queue
is empty or full.
if there is exactly one entry in the queue, then
the front index will equal the rear index.
7

15. Implementations of Queues
When this one entry is removed, then the front
will be increased by 1, so that an empty queue is
indicated when the rear is one position before
the front.
Now suppose that queue is nearly full. Then the
rear will have moved well away from the front, all
the way around the circle.
Queue with one 7 8 9
empty position

16. Implementations of Queues
When the array is full the rear will be exactly one
position before the front.
Full Queue 7 12 8 9
Now we have another difficulty: the front and rear
indices are in exactly the same relative positions
for an empty queue and full queue.
Empty Queue

17. Implementations of Queues : Static
One possible queue implementation is an array.
Elements are added to the end of the queue, but
They may be removed from its beginning, thereby releasing array
cells.
These cells should not be wasted. Therefore,
They are utilized to enqueue new elements,
Whereby the end of the queue may occur at the beginning of the
array. firs
last
This situation is pictured in following figure 4
8
 The queue is full if the first element 2
immediately precedes in the 6
counterclockwise direction the last element. 10 11 15

18. Implementations of Queues : Static
However, because a circular array is implemented with a
“normal” array,
The queue is full if either the
– First element is in the first cell and the last element is in the last
cell. first last
4 2 15 11 10 6 8
– or if the first element is right after the last
last first
10 6 8 4 2 15 11

19. Implementations of Queues : Static
Similarly, enqueue() and dequeue() have to consider
the possibility of wrapping around the array when
adding or removing elements.
E.g. enqueue() can be viewed as operating on a
circular array, but in reality, it is operating on a one
dimensional array. Therefore,
If the last element is in the last cell and if any cells are
available at the beginning of the array,a new element
is placed there.
first last last first
enqueue(6)
2 4 8 6 2 4 8

20. Implementations of Queues : Static
If the last element is in any other position, then the
new element is put after the last, space permitting.
first last first last
enqueue(6)
2 4 8 2 4 8 6
These two situations must be distinguished when
implementing a queue viewed as a circular array.
first
first 2
2
enqueue(6) 4
4
8
8 6
last last

21. Implementations of Queues : Static
template<class T, int size = 100>
class ArrayQueue {
public:
ArrayQueue() { InRef = OutRef = -1; }
void enqueue(T);
T dequeue();
bool isFull() { return OutRef == 0 && InRef == size-1 ||
OutRef == InRef + 1; }
bool is Empty() { return OutRef == -1; }
private:
int InRef, OutRef;
T storage[size];
};

22. Insert Element in a Queue : Static
void template<class T, int size > ArrayQueue<T, size> :: enqueue(T el)
{ if(!isFull())
if(InRef == size –1 || InRef == -1) {
storage[0] = el;
InRef = 0;
if(OutRef == -1)
OutRef = 0;
}
else storage[++InRef] = el;
else
cout << “Full queue. n”;
}

23. Remove Element From a Queue
T template<class T, int size > ArrayQueue<T, size> :: dequeue()
{ T tmp;
if(!isempty())
{
tmp = storage[OutRef];
if(InRef == OutRef)
InRef = OutRef = -1;
else if (OutRef== size – 1)
OutRef = 0;
else OutRef++;
return tmp;
}
else
cout<<“queue is empty”;