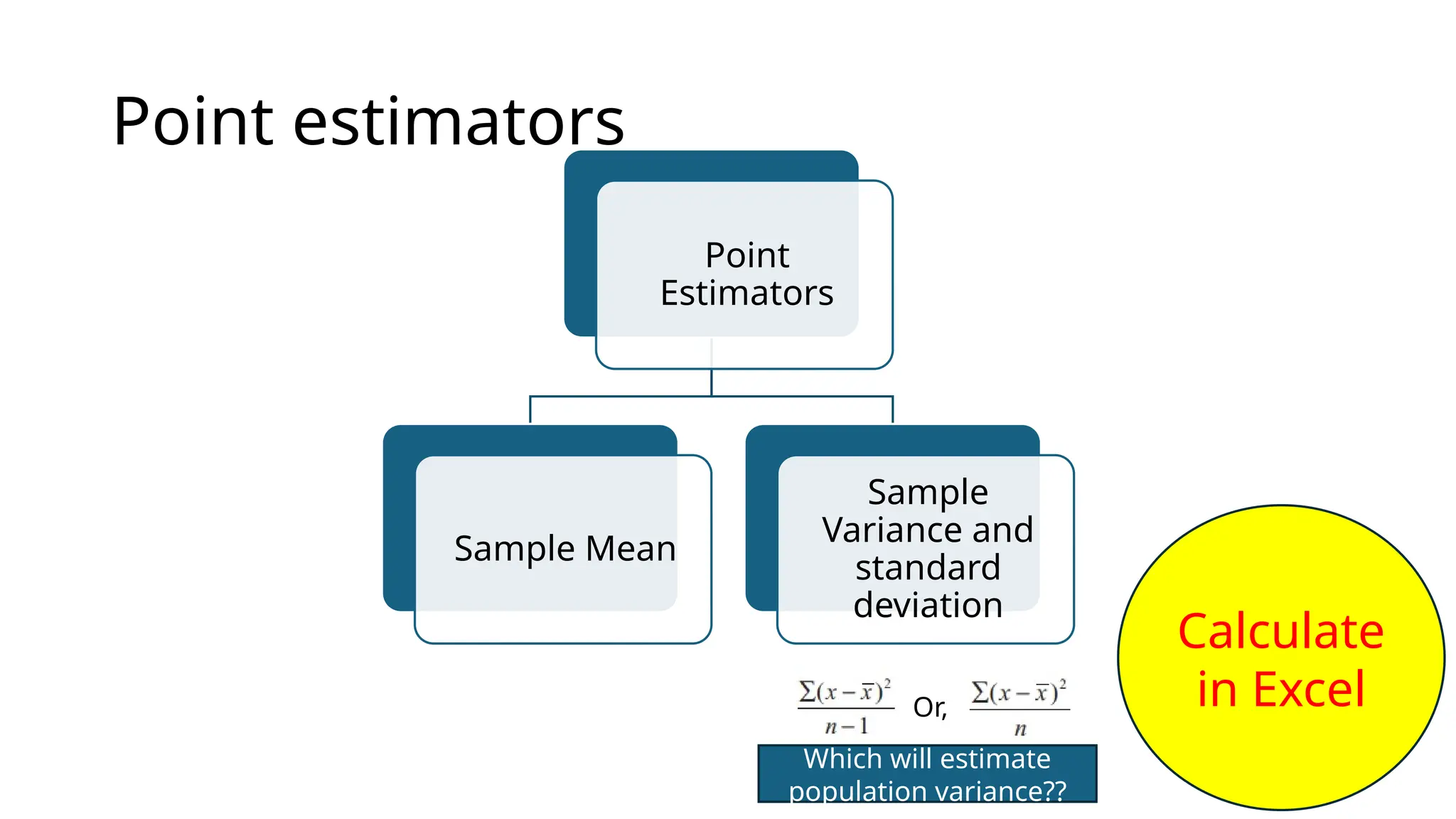
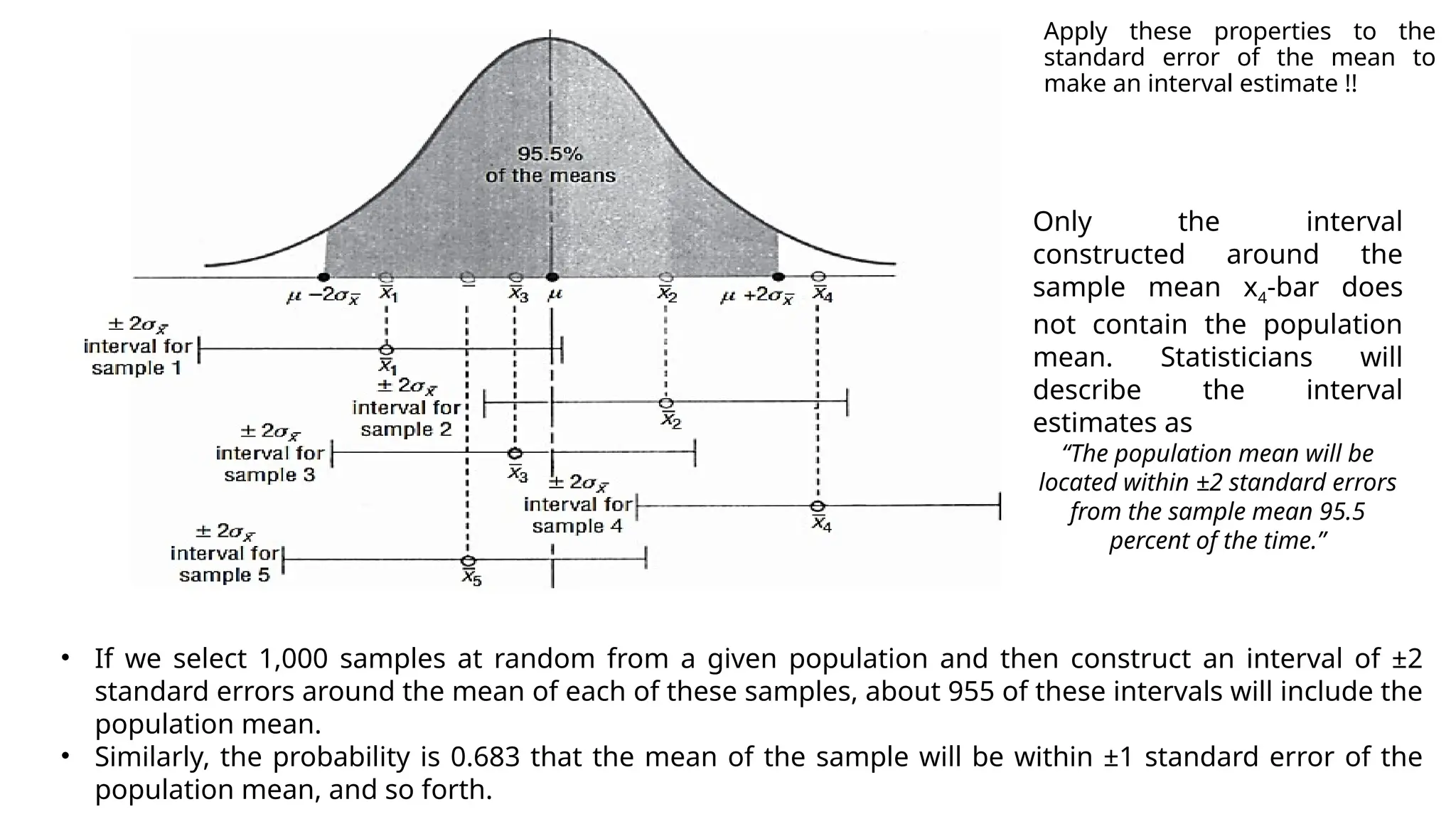
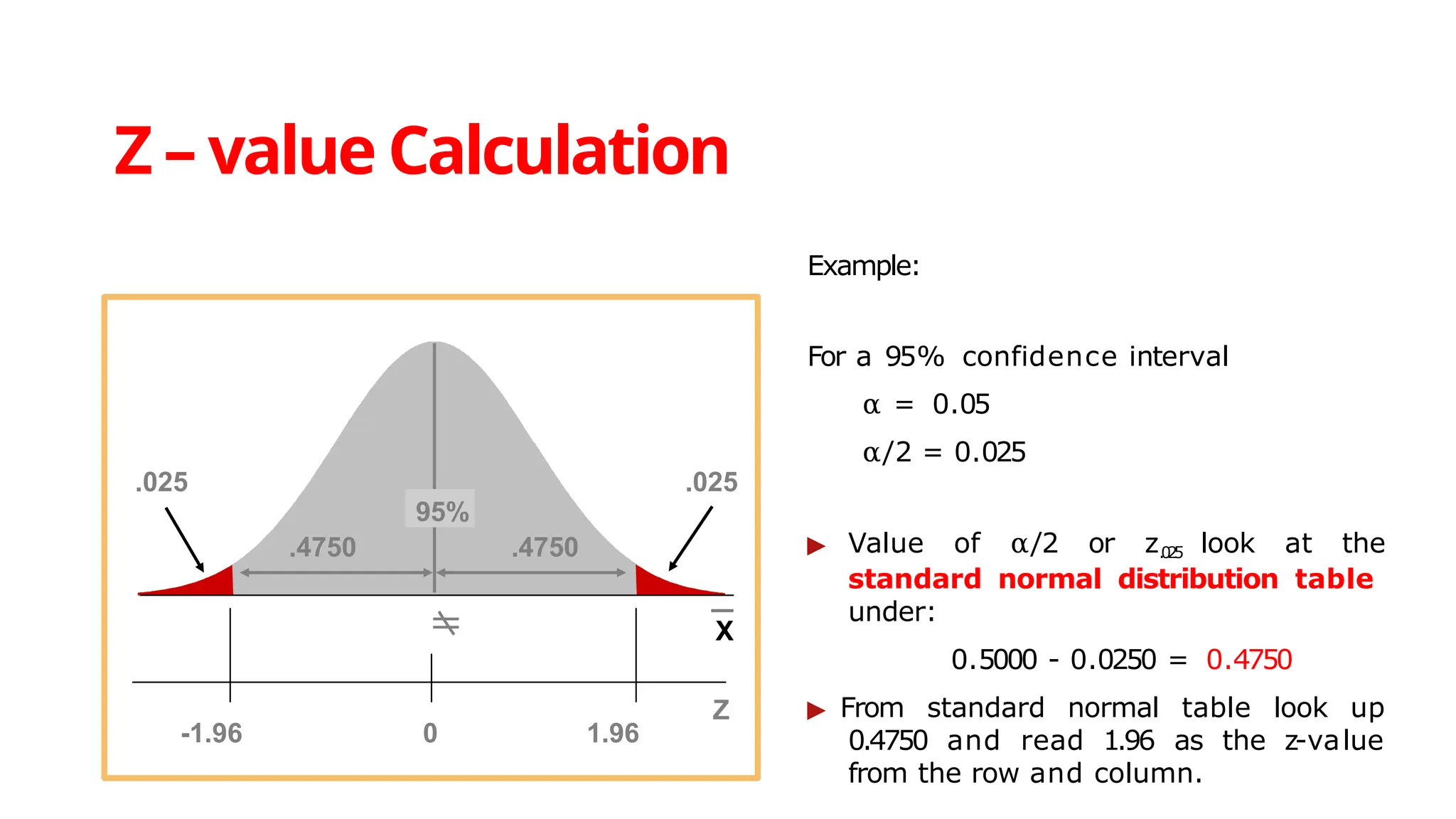
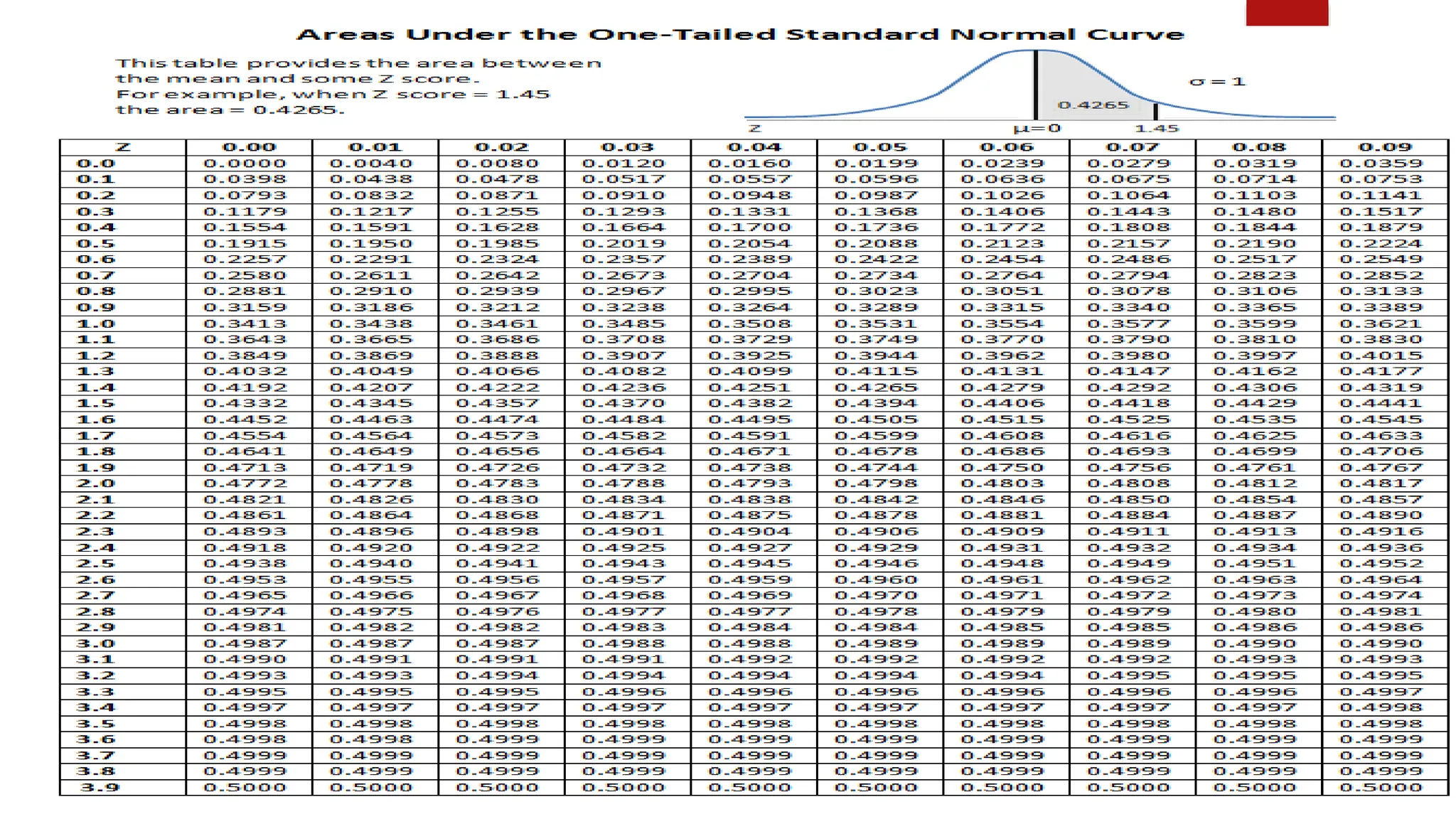
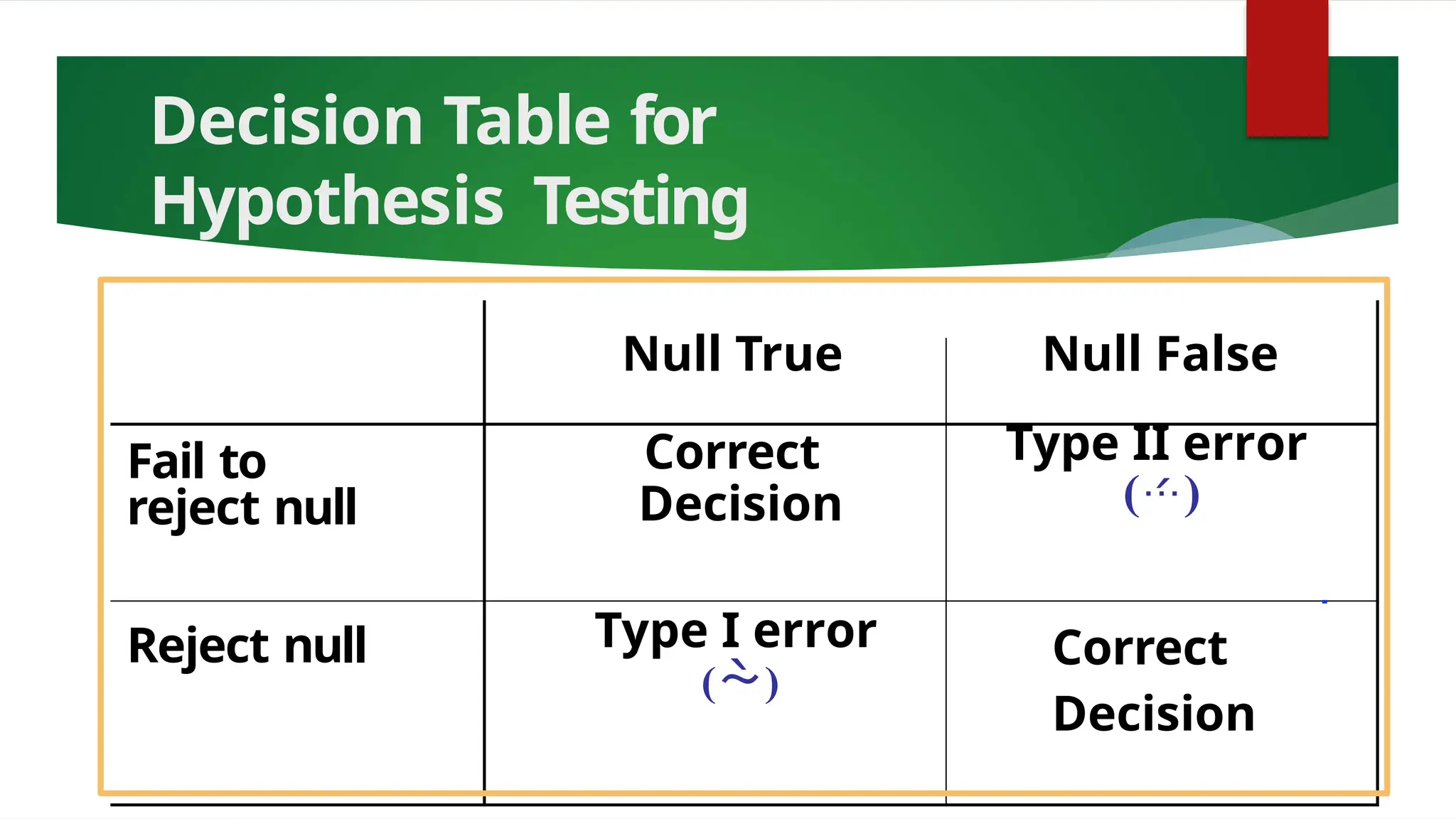
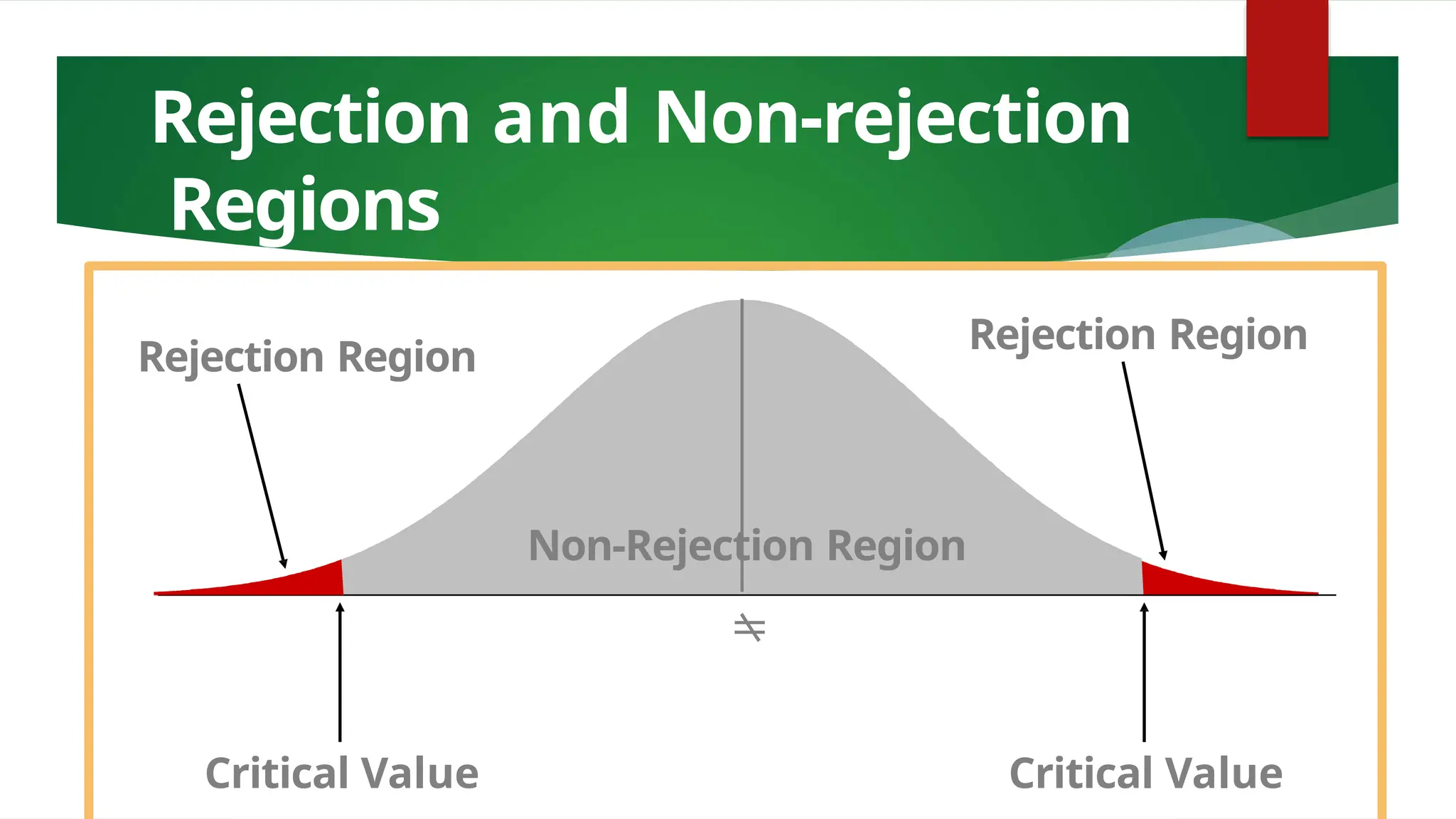
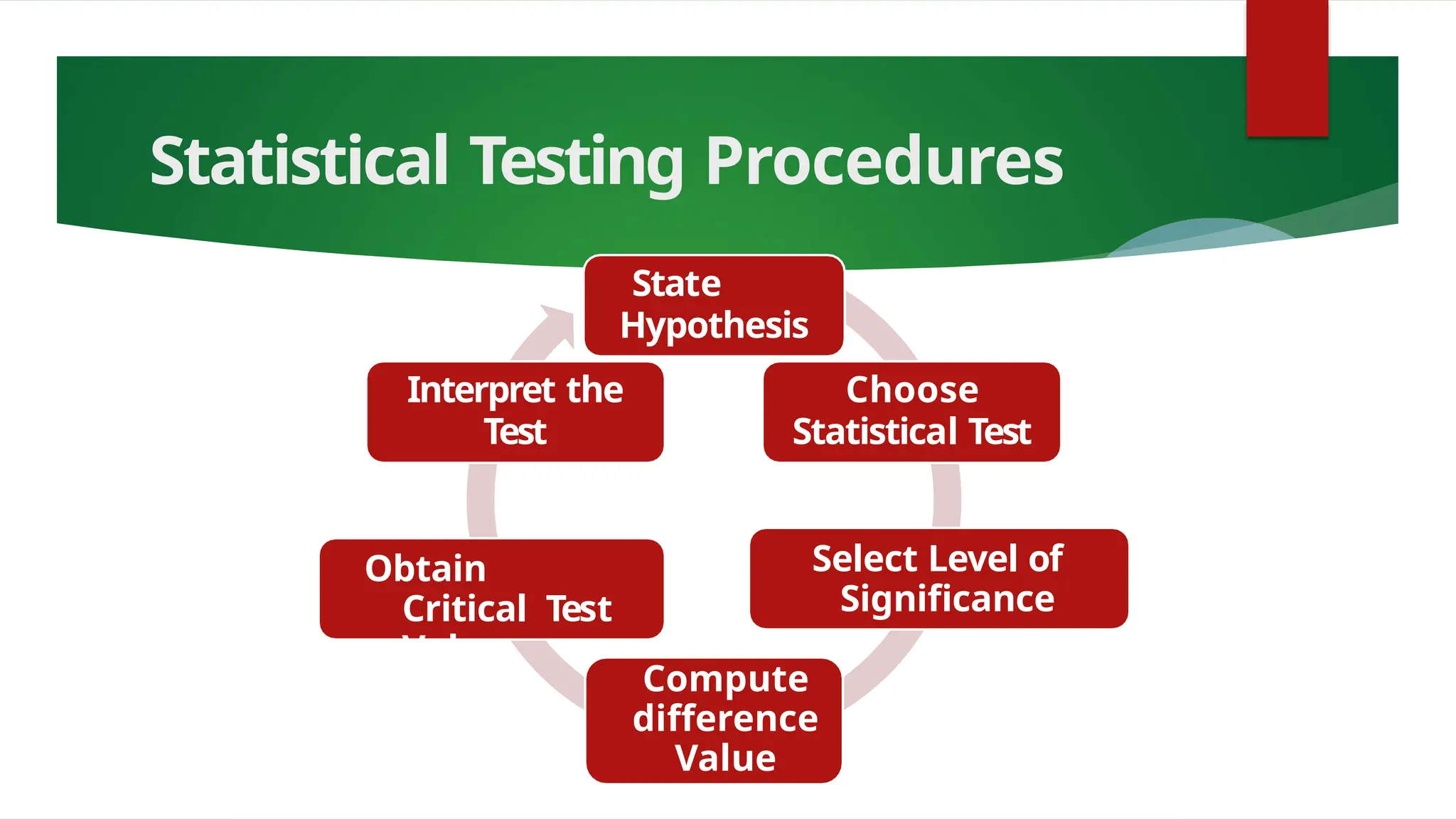
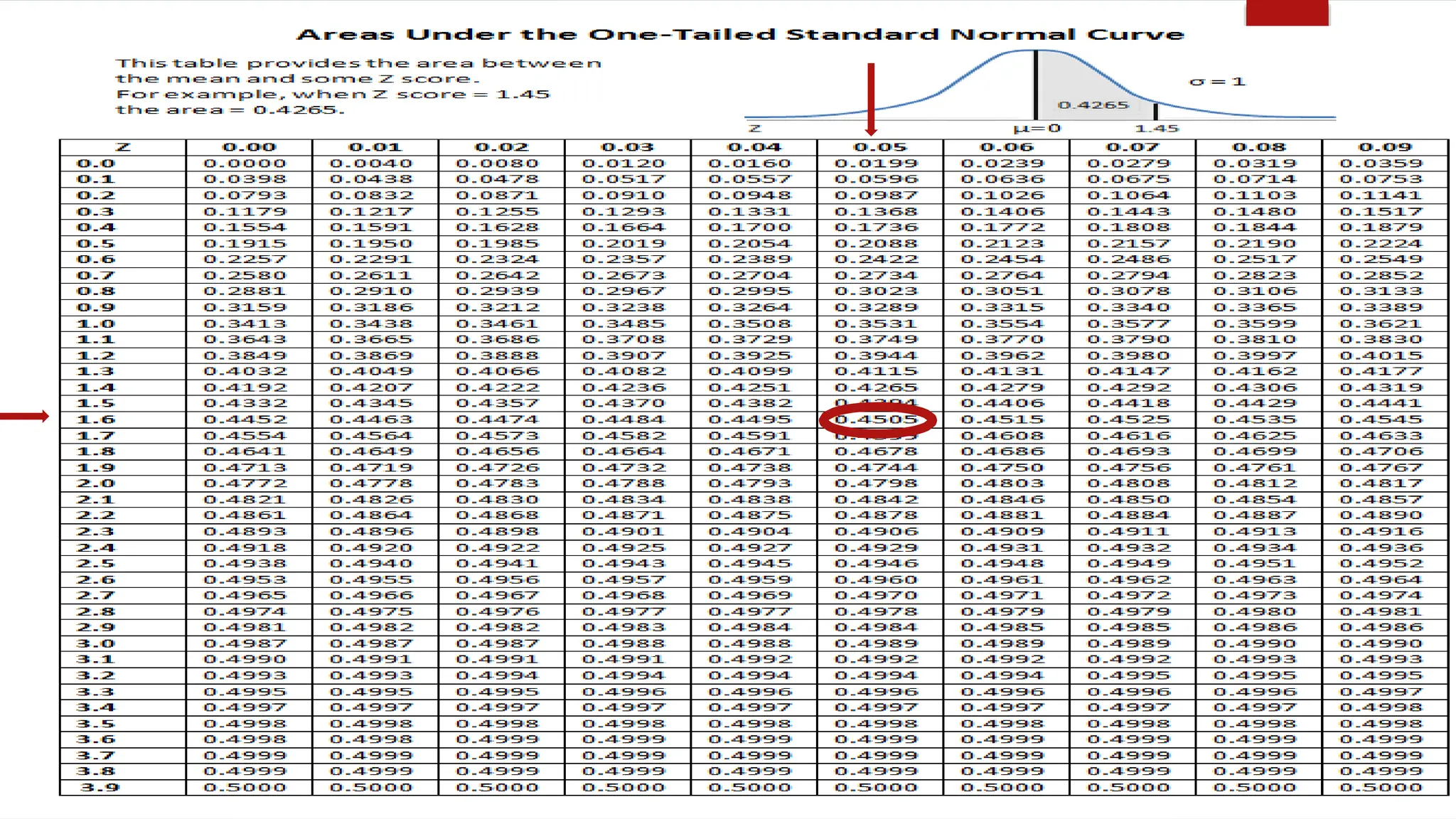
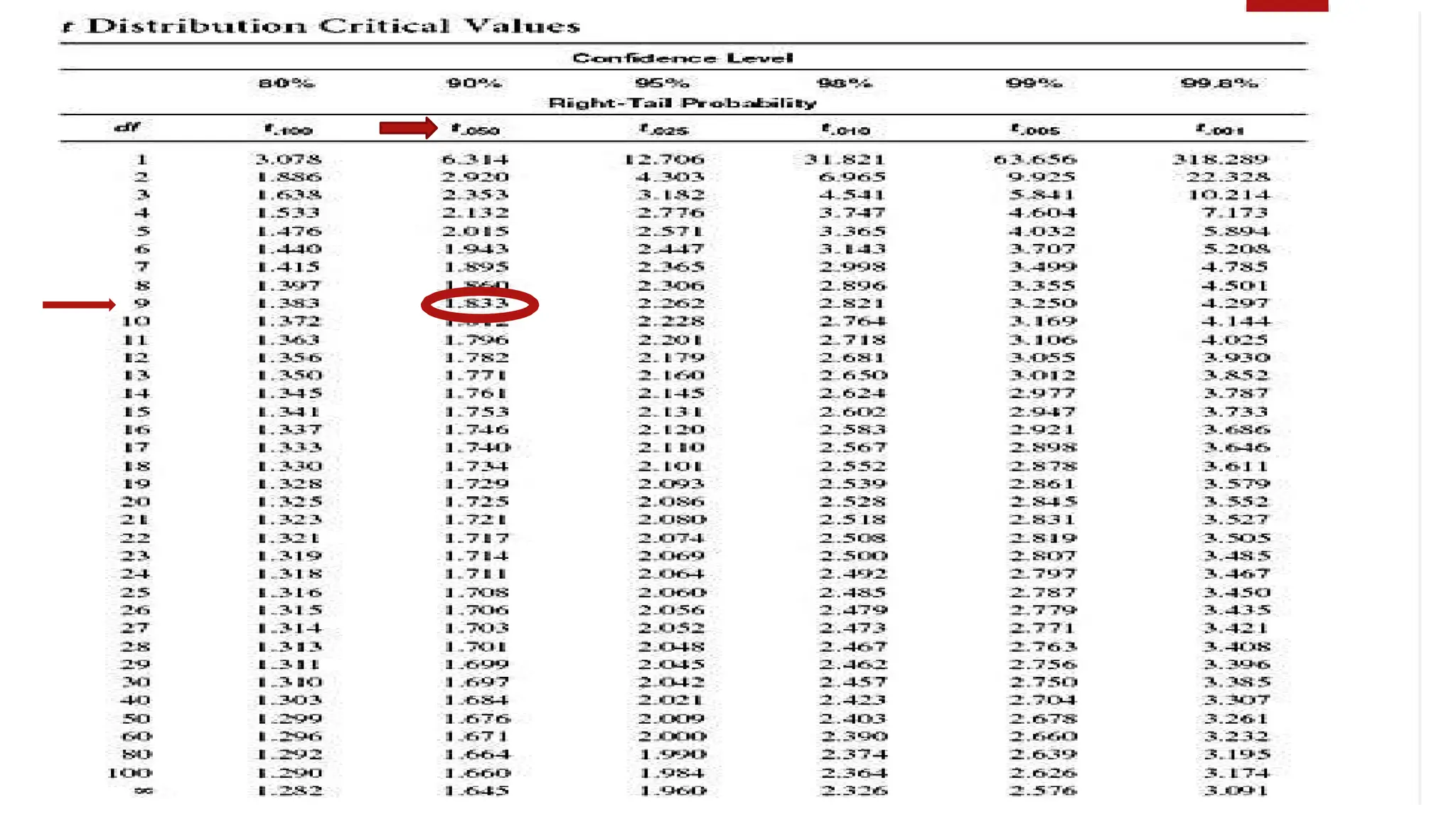
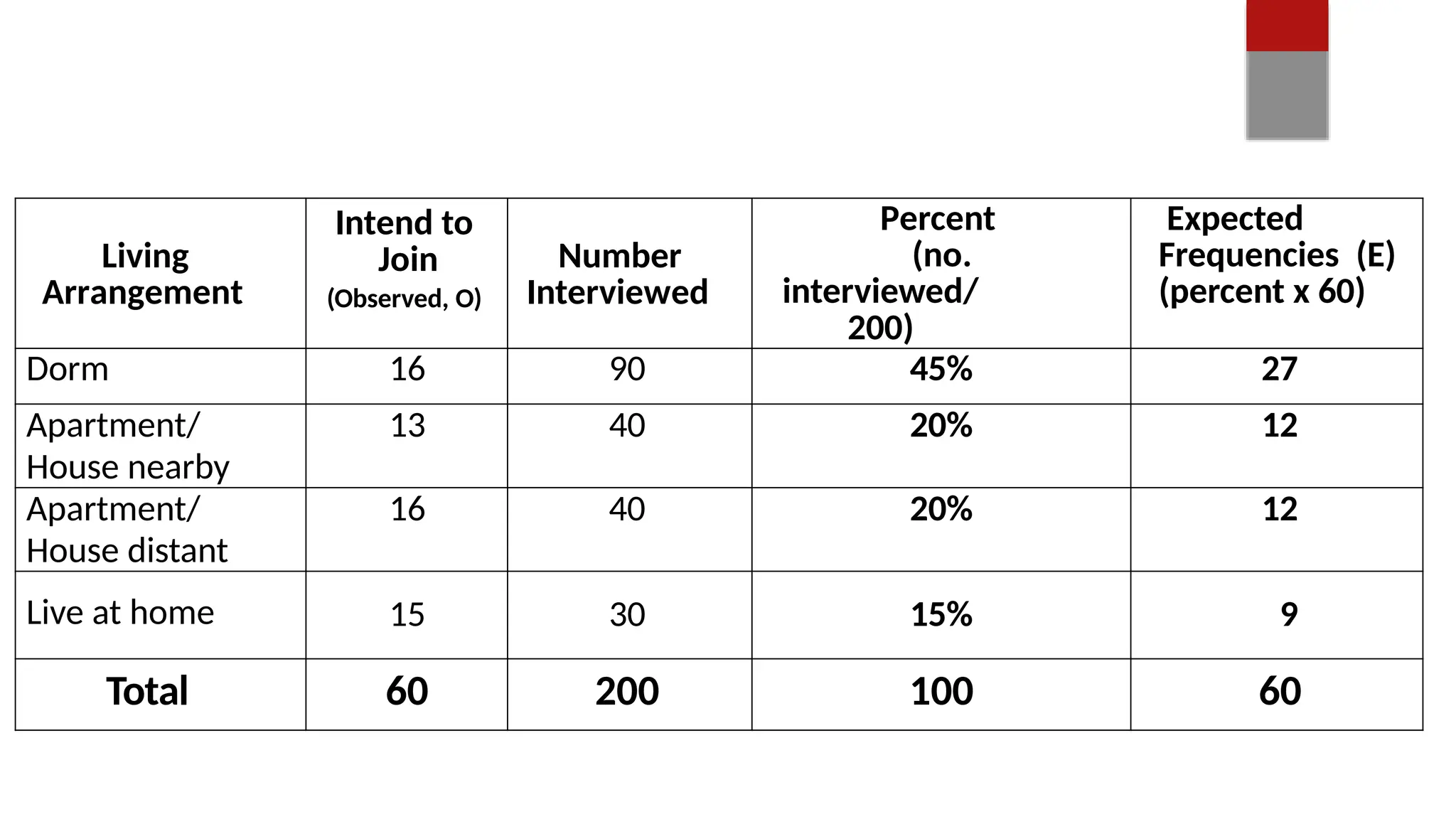
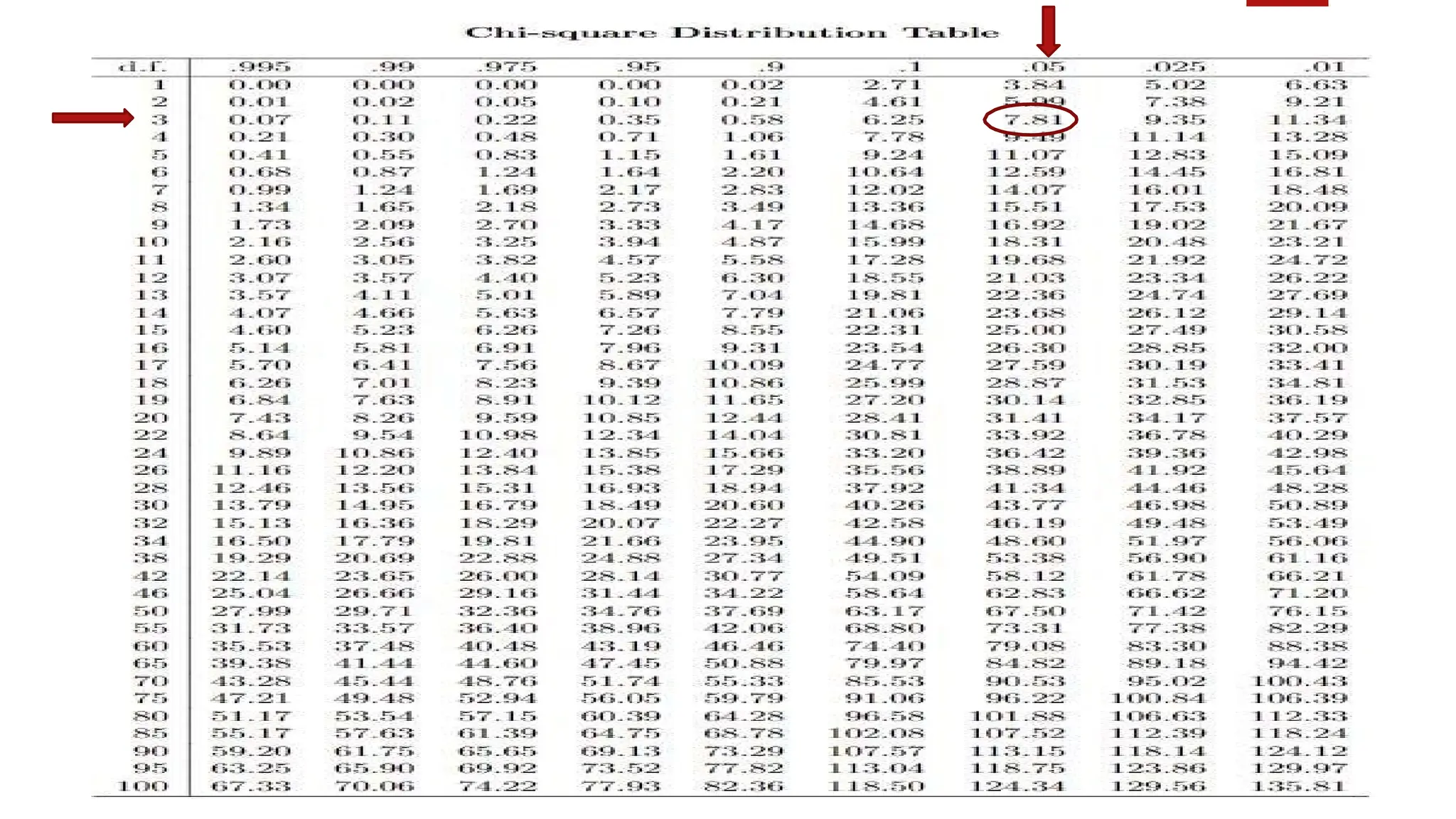
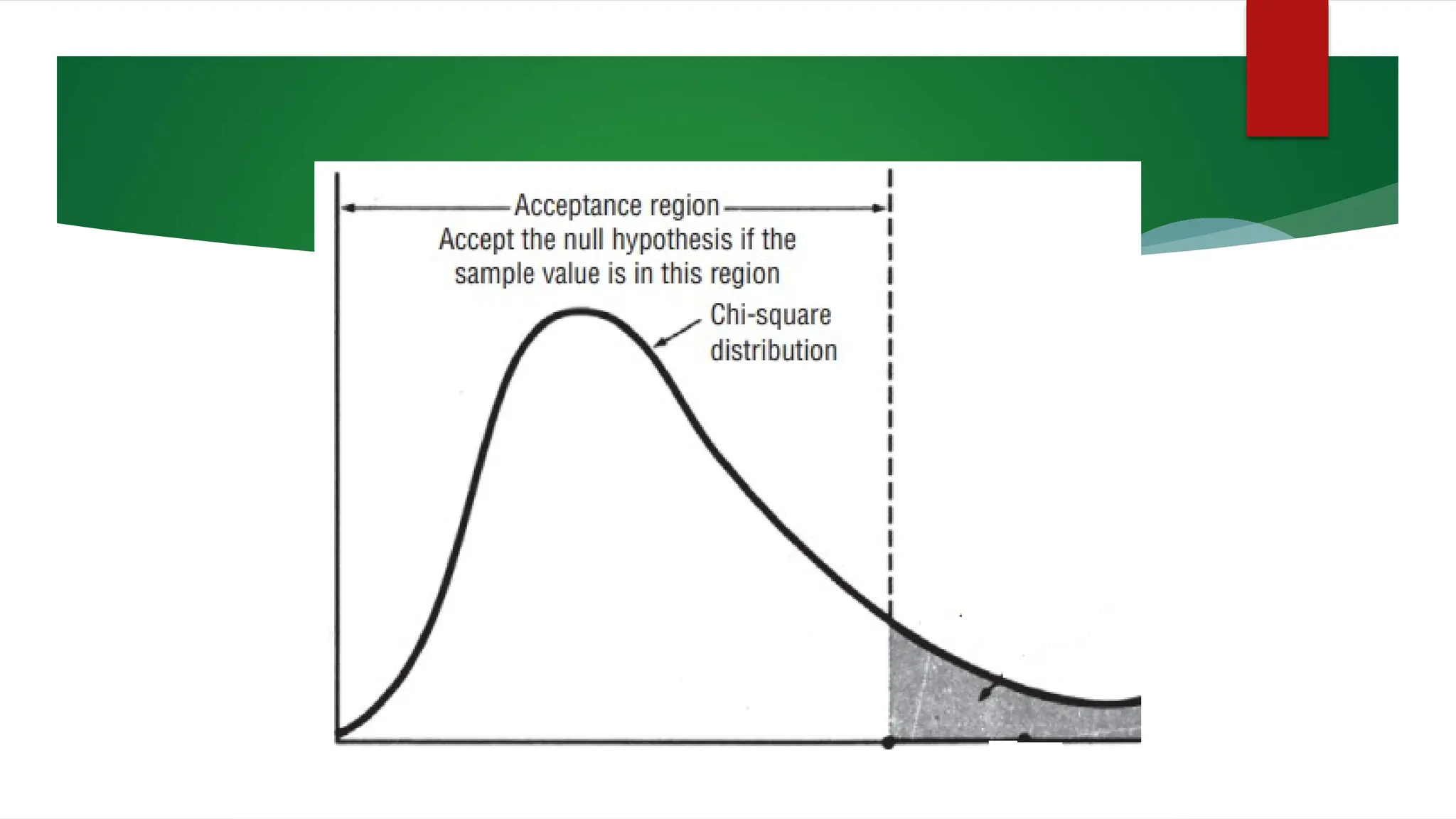
The document discusses various data analysis tools and techniques, focusing on descriptive statistics, exploratory data analysis, and confirmatory data analysis. It emphasizes methods such as point and interval estimation, hypothesis testing, and statistical inference to evaluate population parameters. Specific examples illustrate how estimates and statistical tests can inform decision-making in practical scenarios.