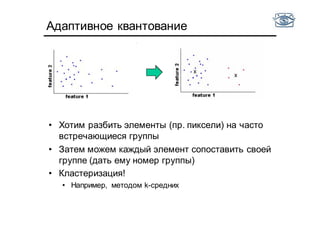
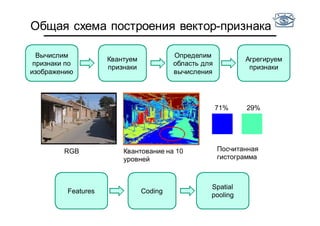
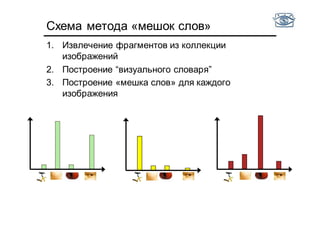
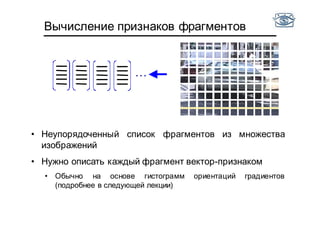
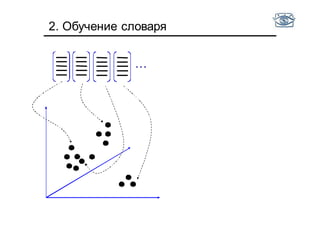
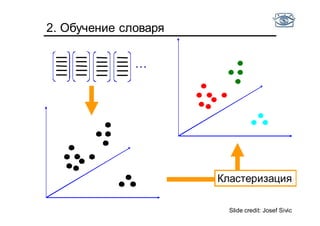
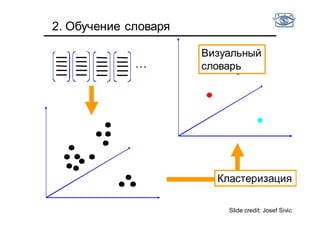
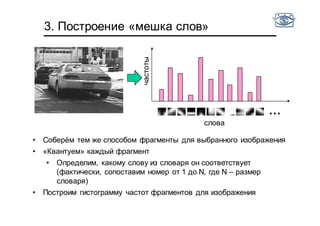
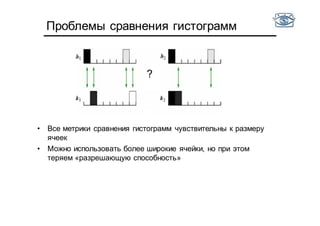
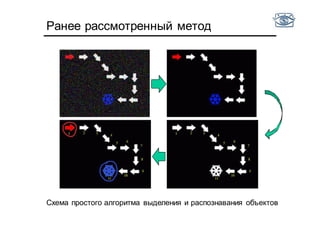
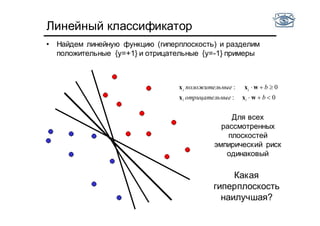
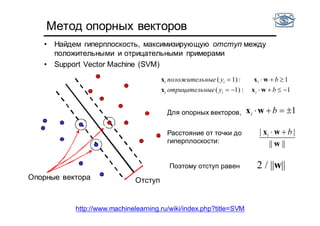
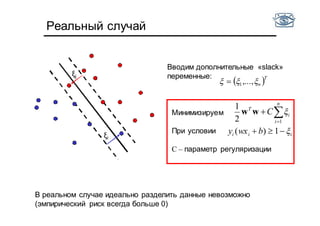
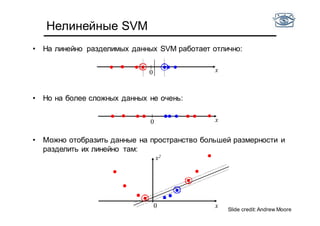
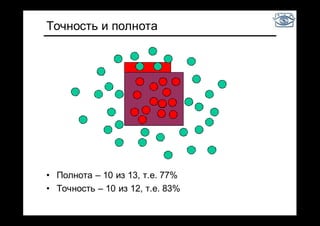
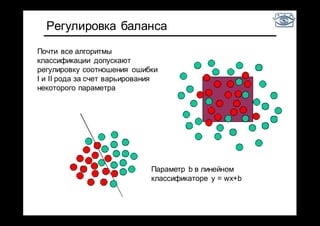
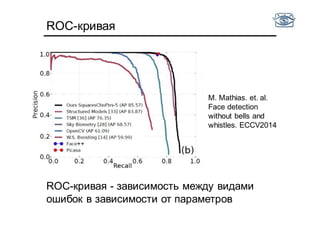
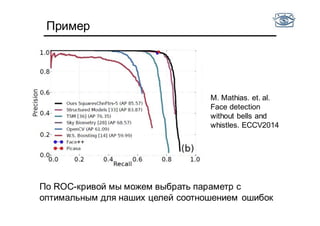
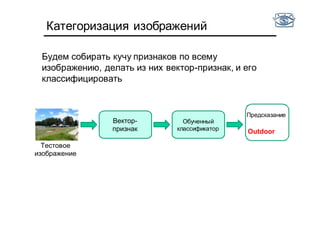
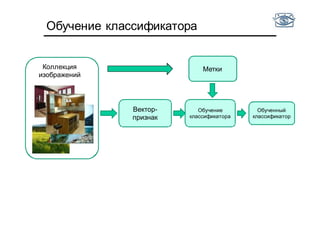
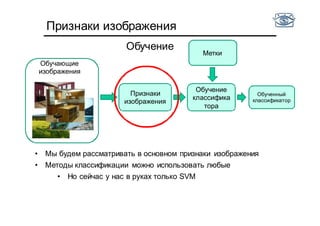
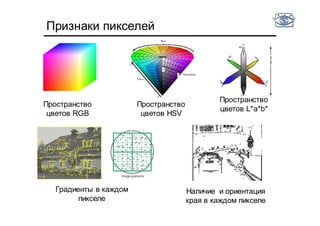
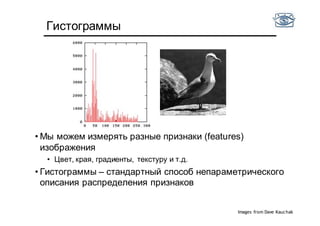
Документ представляет собой лекцию по классификации изображений и машинному обучению, обсуждая методы выделения и распознавания объектов. Основное внимание уделяется методу опорных векторов (SVM) как способу классификации данных, включая детали о линейной и нелинейной классификации. Также рассматриваются важные аспекты оценки предсказательной способности классификаторов, включая ошибки первого и второго рода, а также различные подходы к их минимизации.

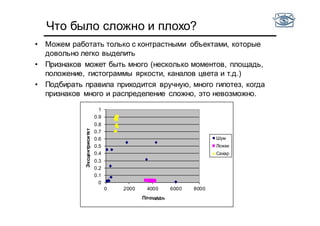
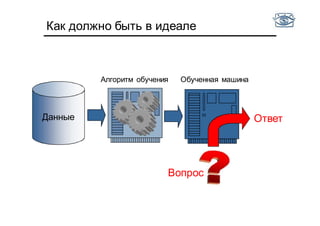



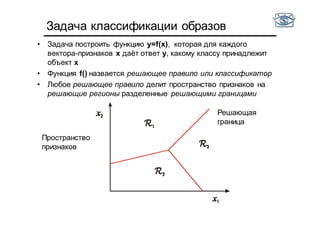
![Классификация
• Будем выбирать функции ft из параметрического
семейства F (т.е. будем выбирать подходящий набор
параметров t)
• Введем некоторую функцию потерь L(ft(x,t), y),
• В случае классификации часто используют
,где - предсказанный класс
• Можем использовать и другие функции потерь
• Задача обучения состоит в том, чтобы найти набор
параметров t классификатора f, при котором потери для
новых данных будут минимальны
• «Метод классификации» = параметрическое семейство F +
алгоритм оценки параметров по обучающей выборке
( ( ), ) [ ( )]L f y I y f x x
( )f x](https://image.slidesharecdn.com/cv201504recognition-150701173034-lva1-app6891/85/CV2015-4-9-320.jpg)


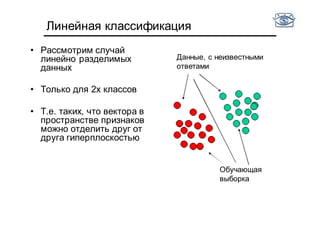
















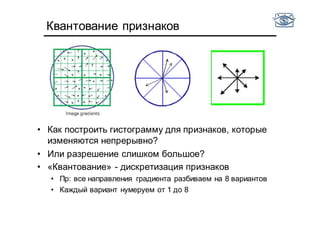
![Квантование признаков
• Есть фотографии тигров и медведей
• Хотим научиться отличать одни от других по цвету
• Оптимально ли использовать гистограмму цветов на
интервале от [0,255]?
• Не все цвета встречаются!](https://image.slidesharecdn.com/cv201504recognition-150701173034-lva1-app6891/85/CV2015-4-48-320.jpg)