Downloaded 41 times
![Matlab + Vlfeat
Вычисление особых точек +
дескриптора
• [fa, da] = vl_sift(Ia) ;
• [fb, db] = vl_sift(Ib) ;
Вычисление сопоставления
• [matches, scores] =
vl_ubcmatch(da, db) ;
49](https://image.slidesharecdn.com/l05features-111031000332-phpapp01/85/L05-features-49-320.jpg)
Uploaded byVictor Kulikov
L05 features
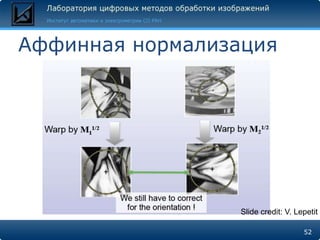
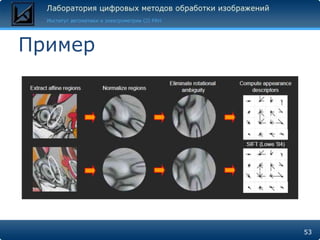
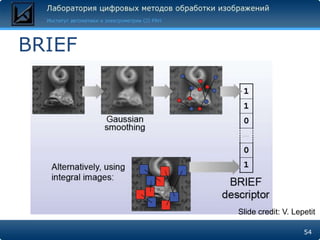
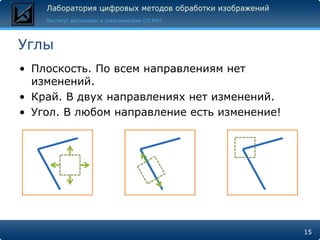
Документ описывает методы поиска и сравнения объектов на изображениях с использованием локальных особенностей, таких как углы и пятна, для обеспечения инвариантности к искажениям и изменениям освещения. Основные алгоритмы, включая Harris, SIFT и MSER, представлены с акцентом на их реализацию в OpenCV и MATLAB. Документ также затрагивает принципы работы дескрипторов, которые делают каждую точку уникальной и устойчивой к изменению условий съемки.
L05 features
- 1. Поиск локальных особенностей Сайт курса: http://cvbeginner.blogspot.com/ 1
- 2. Из прошлой лекции… •Инвариантность • Градиенты • Матрица ковариации 2
- 3. Как найти илисравнить объекты? • Имеем два изображения, содержащие объекты. Мы хотим ответить на вопрос «Содержат ли изображения одинаковые объекты или нет?» 3
- 4.
- 5. Прямое сопоставление (корреляция) •OpenCV – cv::matchTemplate(x,y,res,CV_TM_CCO RR_NORMED); • Matlab – corr2(x,y) • Что делать если изображения имеют разный масштаб? 5
- 6. Многомасштабное представление • Строимпирамиду изображений, где каждое последующее меньше в два раза предыдущего • Проводим сопоставление по всем маштабам 6
- 7. Многомасштабное представление • OpenCV – buildPyr(im,levels,maxlevel) • Matlab – Библиотека vlfeat.org – imup(I) – imdown(I) 7
- 8. Модель преобразований • Геометрические – Поворот – Смещение – Масштабирование • Изменение яркости 8
- 9. А если объектзакрыт или с другого ракурса? 9
- 10. Локальные особенности • Найтиточки на объекте, которые будут на обоих снимках 10
- 11. Где используется • Созданиемозаик • Стерео отождествление • Трассировка • Классификация и поиск 11
- 12. Требования к особенностям •Повторяемость – Особенность находится в том же месте не смотря на изменения точки обзора и освещения • Значимость – У каждой особенности может быть уникальное описание • Локальность – Особенность занимает маленькую площадь и устойчива к перекрытиям • Компактность и эффективность 12
- 13. Что можно выбратьв качестве особенности? 13
- 14. Типы локальных особенностей •Углы • Пятна(Блобы) • Области Вопрос: почему углы? 14
- 15. Углы • Плоскость. Повсем направлениям нет изменений. • Край. В двух направлениях нет изменений. • Угол. В любом направление есть изменение! 15
- 16. Детектор Харриса • C.Harrisand M.Stephens. "A Combined Corner and Edge Detector.” Proceedings of the 4th Alvey Vision Conference: pages 147—151, 1988 • Свойства угла – Градиент имеет два направления – Повторимы и различимы 16
- 17. Основная идея • Вычисляемпроизводные • Считаем в области матрицу ковариации • По соб. числам матрицы М можем сказать принадлежит ли область углу, границе или плоскости 17
- 18. Отклик Slide credit: Антон Конушин 18
- 19. Алгоритм 1. Считаем производные 2.Для каждого пикселя считаем матрицу ковариации M в окне 3. Вычисляем dst(x,y) 4. Режим по порогу dst(x,y) 5. Ищем локальные максимумы в окне 19
- 20.
- 21. Реализация • OpenCV – cv::cornerHarris(y,res,4,3,0); – cv::goodFeaturesToTrack(y, corners, 200, 0.15, 5,cv::Mat(), 3,true, 0.04 ); • Matlab – vl_harris(I) 21
- 22. Свойства детектора Харисса •Инвариантность к повороту • К смещению • Частичная инвариантность к изменению яркости 22
- 23. Инвариантность к масштабу •Найти признаки инвариантные к изменению масштаба • Мы знаем как найти границу 23
- 24.
- 25. Пятна (Блобы) • Точкаили пятно имеющее вид круга – хорошая особая точка. 25
- 26. Поиск пятен Slide credit: Антон Конушин 26
- 27. Чтобы найти пятно •Чтобы найти пятно надо свернуть сигнал с Лапласианом соответствующей дисперсией • Проблема: при повышении дисперсии уменьшается отклик на идеальный край 27
- 28. Нормализация • Умножая лапласианна дисперсию в квадрате этот эффект пропадает 28
- 29. Многомасштабность • Свертываем снормализированным Лапласианом в разных масштабах • Ищем максимумы функции по всем масштабам 29
- 30. Поиск пятен 30
- 31. Реализация • OpenCV – SIFT • Matlab – vl_sift(d) • Считается эффективно, на пирамиде изображений 31
- 32. Области MSER • Сегментироватьпо порогу яркости • Для всех областей найти порог, чтобы рост площади области был минимален • Описать эти области эллипсами 32
- 33.
- 34.
- 35. Реализация • OpenCV – MSER • Matlab – vl_mser 35
- 36. Итого • Необходима инвариантностьк искажениям • Углы и пятна – разные множества, можно использовать совместно 36
- 37.
- 38. Дескрипторы • Хотелось бычтобы каждую точку можно было отличить от другой • При этом описание практически не завесило от геометрических искажений Slide credit: Антон Конушин 38
- 39. Дескрипторы d=(d1,d2,…dn) 39
- 40. Дескрипторы должны быть: •специфичны (отличаем разные точки) • локальны (зависеть только от небольшой окрестности) • инвариантны (к искажениям/изменению освещенности) • просты в вычислении 40
- 41. Прямое сопоставление Дескриптор: Векторинтенсивностей пикселей окрестности 41
- 42. Прямое сопоставление • Сравниваемкак сумма квадратов или модулей разности • Работает только простой сдвиг • Для достижения инвариантности по яркости надо нормировать – I=(I-mean(I))/std(I) • Недостатки? 42
- 43. SIFT Scale-Invariant Feature Transform: •Детектор DoG (быстрая вариация поиска Пятен) • Определение положения и масштаба особенности Ориентация • Определение доминантной ориентации по градиентам Дескриптор • Использование статистик по направлению градиентам • Устойчив к изменениям освещенности и небольшим • Сдвигам David G. Lowe. "Distinctive image features from scale- invariant keypoints.” IJCV 60 (2), pp. 91-110, 2004. 43
- 44. Ориентация Slide credit: Антон Конушин 44
- 45.
- 46. Гистограмма градиентов Вычисляем градиентв каждом пикселе • Строим гистограммы направлений градиентов по прямоугольным областям • Вклад каждого пикселя взвешиваем по гауссиане с центром в центре окрестности • Обычно – сетка 4x4, в каждой гистограмма с 8ю ячейками • Стандартная длина вектора-дескриптора – 128 (4*4*8) • Сравниваем как вектор (разные метрики) 46
- 47.
- 48. Реализация Opencv • Features2d _featureDetector= cv::FeatureDetector::create( "FAST" ); _descriptorExtractor = cv::DescriptorExtractor::create( "SURF" ); _descriptorMatcher = cv::DescriptorMatcher::create( “BruteForce- Hamming”); std::vector<cv::KeyPoint> kp; _featureDetector->detect(grey,kp); cv::Mat queryDescriptors; _descriptorExtractor->compute( grey, kp, queryDescriptors ); vector<DMatch> matches; if(!_descriptorMatcher->empty()) { _descriptorMatcher->match( queryDescriptors, matches ); }else{ _descriptorMatcher->add( queryDescriptors); 48
- 49. Matlab + Vlfeat Вычислениеособых точек + дескриптора • [fa, da] = vl_sift(Ia) ; • [fb, db] = vl_sift(Ib) ; Вычисление сопоставления • [matches, scores] = vl_ubcmatch(da, db) ; 49
- 50. Итого • Дескриптор SIFTвесьма специфичен, устойчив к изменениям освещения, небольшим сдвигам • Вся схема SIFT (детектор, выбор окрестностей, дескриптор) оказалась очень эффективным инструментов для анализа изображений • Очень широко используется 50
- 51. Перспективные преобразование Slide credit: Антон Конушин 51
- 52. Аффинная нормализация Slide credit: V. Lepetit 52
- 53. Пример 53
- 54. BRIEF Slide credit: V. Lepetit 54
- 55. SIFT + MSER Slide credit: Zisserman 55
- 56.
- 57. Вопросы 57