Uploaded byAnton Konushin
CV2011-2. Lecture 12. Face models.
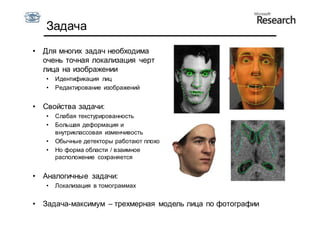
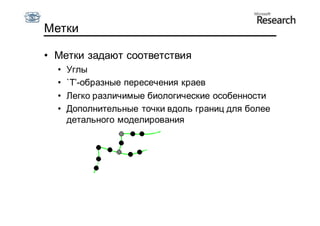
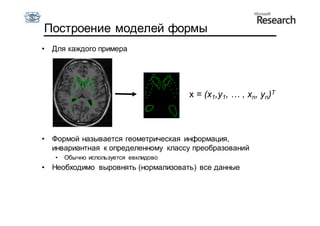
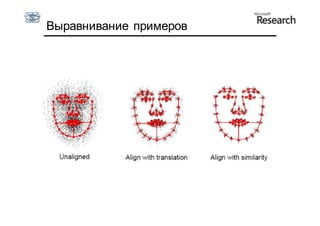
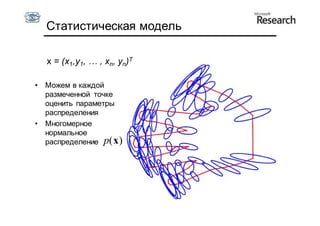
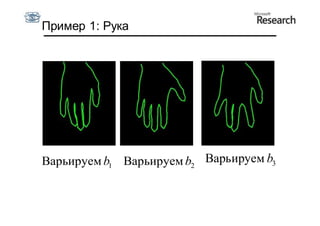
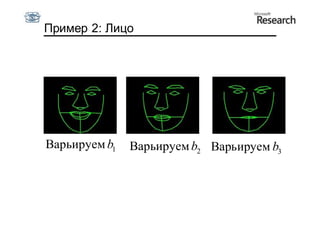
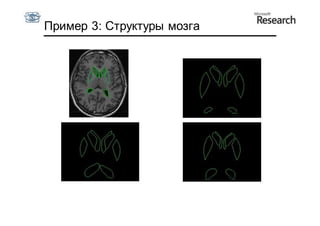
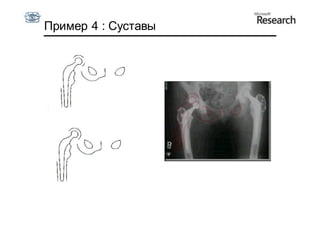
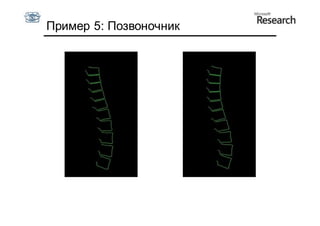
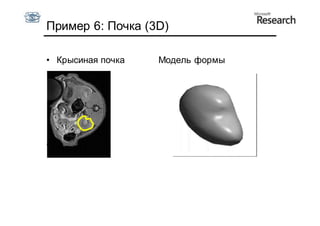
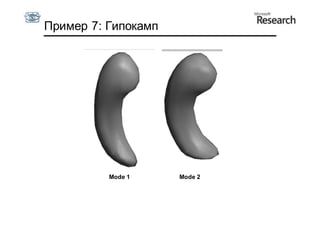
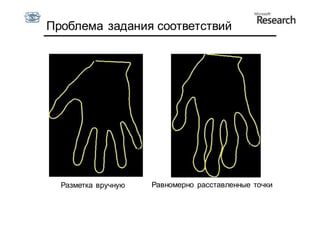
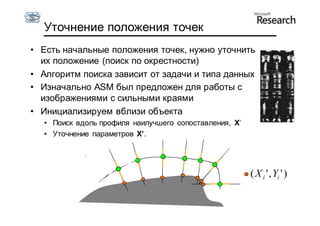
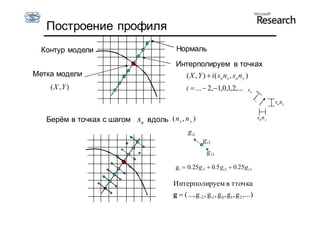
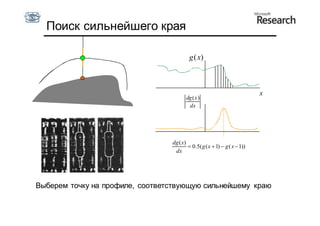
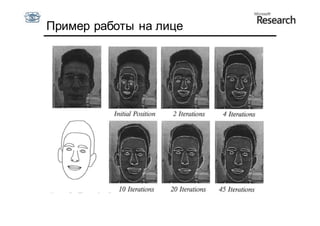
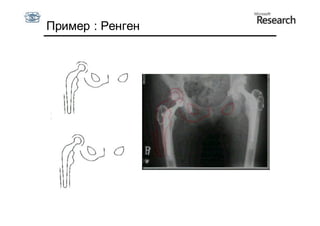
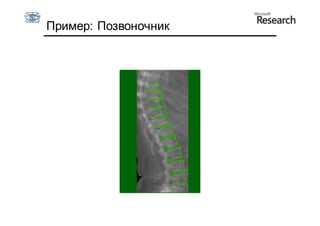
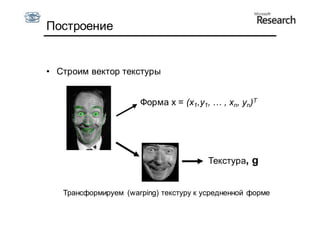
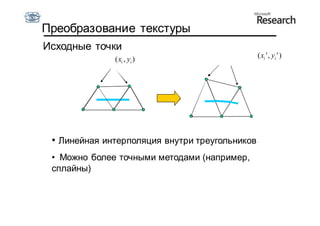
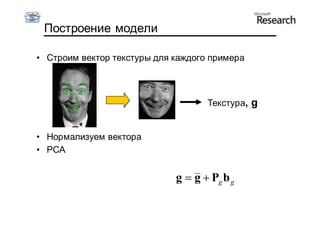
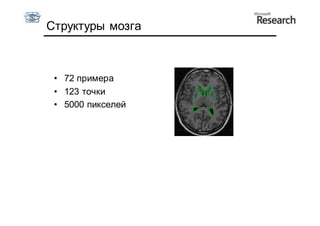
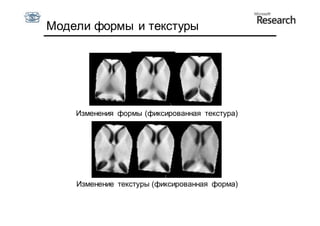
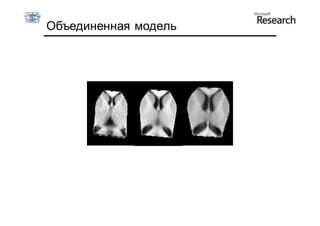
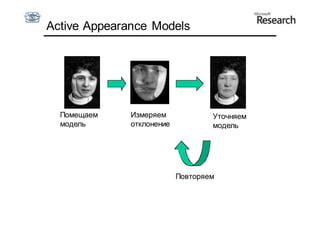
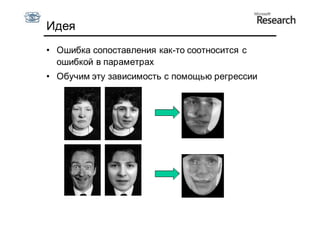
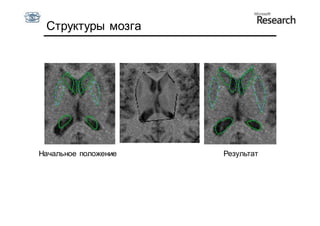
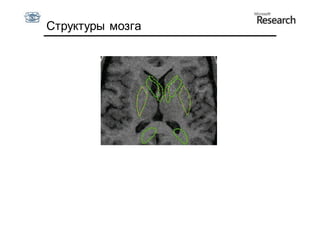
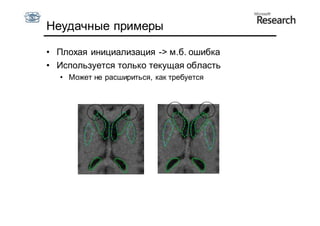
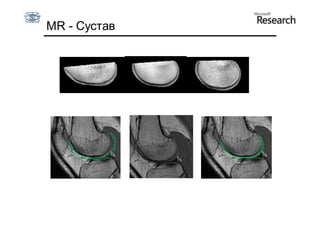
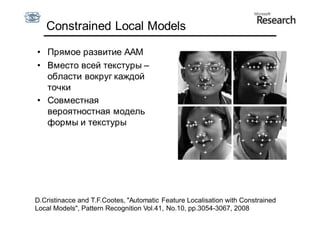
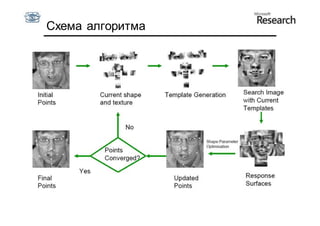
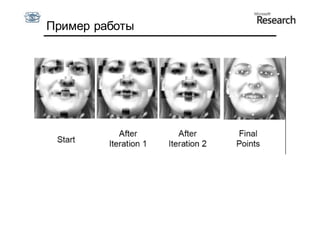
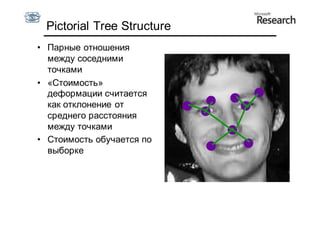
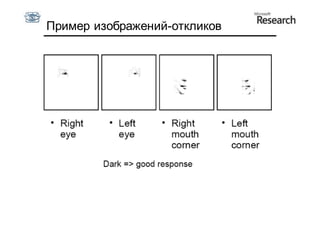
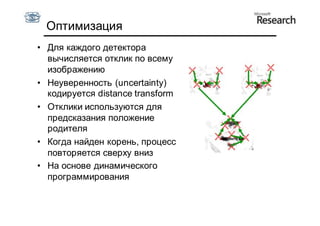
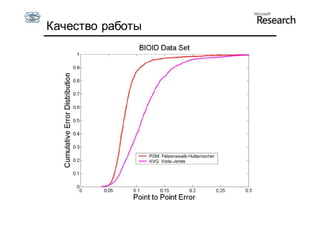
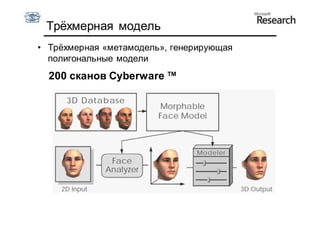
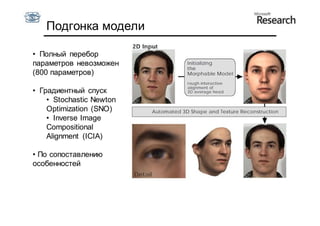
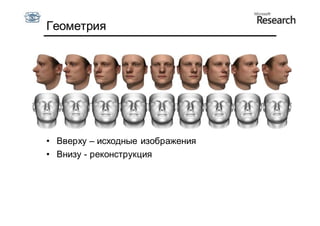
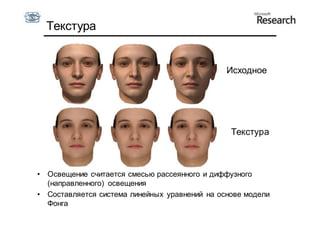
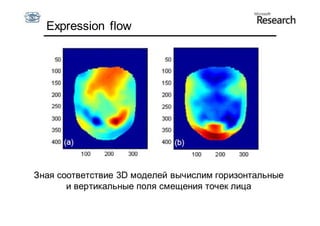
Документ описывает курс по статистическим моделям формы и активным моделям формы лиц, подготовленный при поддержке Microsoft Research, акцентируя внимание на задачах высокоточной локализации черт лица на изображениях. В нем рассматриваются методы, такие как активные модели формы и модели внешности, а также подходы к автоматическому построению моделей и локализации характерных точек на изображениях. Также документ иллюстрирует применение этих моделей в области компьютерного зрения для распознавания лиц и анализа различных структур, таких как руки и суставы.
CV2011-2. Lecture 12. Face models.
- 1. Черты лица имоделирование Антон Конушин http://courses.graphicon.ru/vision2
- 2. Этот курс подготовлен приподдержке Microsoft Research
- 3. Задача • Для многих задач необходима очень точная локализация черт лица на изображении • Идентификация лиц • Редактирование изображений • Свойства задачи: • Слабая текстурированность • Большая деформация и внутриклассовая изменчивость • Обычные детекторы работают плохо • Но форма области / взаимное расположение сохраняется • Аналогичные задачи: • Локализация в томограммах • Задача-максимум – трехмерная модель лица по фотографии
- 4. План лекции • Статистическиемодели формы • Statistical shape models • Active Shape Models (ASM) • Active Appearance Models (AAM) • Локально-ограниченными модели • Constraint Local Models • Pictorial tree structure • 3D модели • Применение методов
- 5. История - EigenFaces x x Pb • Представляем вектор (изображение лица) с помощью многомерного нормального распределения • Переходим к новому представлению – базису в новом пространстве M. Turk and A. Pentland. "Face recognition using eigenfaces". Proc. IEEE CVPR 1991. pp. 586–591.
- 6. Модель формы •Набор размеченных изображений • Метки задают положение характерны точек • Построим статистическую модель T.F. Cootes, C.J. Taylor, D.H. Cooper and J. Graham, Training Models of Shape from Sets of Examples. in Proc. British Machine Vision Conference. Springer-Verlag, 1992, pp.9-18
- 7. Метки • Метки задаютсоответствия • Углы • `T’-образные пересечения краев • Легко различимые биологические особенности • Дополнительные точки вдоль границ для более детального моделирования
- 8.
- 9. Построение моделей формы • Для каждого примера x = (x1,y1, … , xn, yn)T • Формой называется геометрическая информация, инвариантная к определенному классу преобразований • Обычно используется евклидово • Необходимо выровнять (нормализовать) все данные
- 10. Процедура совмещения • «Прокрустов»анализ • Процедура • Совмещаем все экземпляры с первым – Есть соответствие точек! • Повторяем до сходимости – Вычисление средней формы – Нормализация средней формы » Либо совмещением её с первым экземпляром » Либо к какому-либо фиксированному нормальному варианту
- 11. Совмещение 2х экземпляров • Ищем преобразование M, минимизирующее • М – евклидово (масштаб s, поворот и сдвиг) E W | x i M (x i ) |2 • Веса W можно выбирать пропорционально стабильности точки.
- 12. Совмещение 2х экземпляров • Делаем замену • Получаем СЛАУ
- 13.
- 14. Выравнивание примеров Пальцы наруке более подвижны, поэтому веса для них уменьшаем при совмещении
- 15. Статистическая модель x = (x1,y1, … , xn, yn)T • Можем в каждой размеченной точке оценить параметры распределения • Многомерное нормальное распределение p(x )
- 16. Построение моделей формы •Даны выровненные формы {x i } • Применяем МГК (PCA): x x Pb • P – Первые t собственных векторов • b – Параметры модели формы T b P (x x ) • Допустимые пределы варьирования параметров: |bi| 3 λi
- 17. Модель формы -рука • 72 метки поставлены по контуру руки • 18 контуров руки получены путем сравнения с порогов изображений рук на белом фоне • Основные метки выбраны на кончиках пальцев и в ложбинках между пальцами • Остальные равномерно между ключевыми 6 5 4 3 2 1
- 18. Пример 1: Рука Варьируемb1 Варьируем b2 Варьируем b3
- 19. Пример 2: Лицо Варьируемb1 Варьируем b2 Варьируем b3
- 20. Пример 3: Структурымозга
- 21. Пример 4 :Суставы x x p1b1 3 1 b1 3 1
- 22.
- 23. Пример 6: Почка(3D) • Крысиная почка Модель формы • 18 примеров
- 24. Пример 7: Гипокамп Mode 1 Mode 2
- 25. Проблема построения разметки •Автоматическое построение модели • Необходимо задать соответствия между точками большой выборки • Низка надежность автоматического сопоставления • Человек невольно ставит точки «разумно»
- 26. Проблема задания соответствий Разметка вручную Равномерно расставленные точки
- 27. Активная Модель Формы • Пусть у нас есть статистическая модель формы • Как использовать ее для анализа изображений, т.е. для нахождения характерных точек? • Метод “Active Shape Model” • Итеративный метод сопоставления модели изображению • Будем использовать модель формы для локализации области поиска точек • Новые положения точек позволят уточнить параметры модели T.F.Cootes, C.J.Taylor, Active Shape Models - `Smart Snakes'. in Proc. British Machine Vision Conference. 1992, pp.266-275.
- 28. Схема метода • Параметры: T (преобразование), b (параметры модели) • Имеем начальное положение всех точек • Инициализируем T и b • Повторяем до сходимости: • X: Ищем наилучшее положение для каждой точки модели в некоторой окрестности (локальное уточнение) • T: Вычисляем наилучшее преобразование модели в новое положение • b: Разница между моделью и точками используется для обновления параметров модели
- 29. Уточнение положения точек •Есть начальные положения точек, нужно уточнить их положение (поиск по окрестности) • Алгоритм поиска зависит от задачи и типа данных • Изначально ASM был предложен для работы с изображениями с сильными краями • Инициализируем вблизи объекта • Поиск вдоль профиля наилучшего сопоставления, X’ • Уточнение параметров X’. ( X i ' , Yi ' )
- 30. Построение профиля Контур модели Нормаль Интерполируем в точках Метка модели ( X , Y ) i ( s n nx , s n n y ) ( X ,Y ) i ... 2,1,0,1,2,... sn sn n y Берём в точках с шагом sn вдоль ( n x , n y ) snn x g i1 gi 2 gi 3 gi 0. 25gi1 0.5 gi 2 0.25gi 3 Интерполируем в тточка g (..., g -2 , g-1 , g 0 , g1, g 2 ,...)
- 31. Поиск сильнейшего края g ( x) x dg ( x ) dx dg ( x) 0.5( g ( x 1) g ( x 1)) dx Выберем точку на профиле, соответствующую сильнейшему краю
- 32. Модель профиля •Иногда истинное положение не соответствует сильнейшему краю Strongest edge True position • Смоделируем локальную структуру изображения для поиска • Например, модель изображения вдоль профиля • Можем применить PCA/ASM и тут T.F.Cootes, C.J.Taylor, Active Shape Model Search using Local Grey-Level Models: A Quantitative Evaluation, in Proc. British Machine Vision Conference, 1993, pp.639-648
- 33. Учет ограничений модели •Жесткие ограничения • Минимизируем | X T ( x Pb) |2 Dmax 3 • Мягкие ограничения • Минимизируем 1 2 2 | T ( X ) ( x Pb) | / r log( p(b)) • Можем добавить веса, учитывающие качество локального сопоставления
- 34. Многомасштабный поиск • Обучаем локальные модели на каждом уровне пирамиды • Гауссова пирамида с шагом 2 • Используем те же точки • Разные локальные модели T.F.Cootes , C.J.Taylor, A.Lanitis, Active Shape Models : Evaluation of a Multi- Resolution Method for Improving Image Search, in Proc. British Machine Vision Conference, 1994, pp.327-336.
- 35. Многомасштабный поиск • Начинаемс самого низкого разрешения • Для каждого уровня • Поиск вдоль профиля • Обновляем параметры • (Накладываем ограничения на параметры) • Повторяем до сходимости на этом уровне • Пример: • Профиль длины 7 пикселей, 5 уровней пирамиды, 10 итераций на каждом уровне
- 36. Пример работы налице
- 37. Пример : Ренген x x p1b1 3 1 b1 3 1
- 38.
- 39. Выделение черт лица •Можем использовать любые детекторы для поиска характерной точки • Сопоставление шаблонов • Детектор на основе классификатора • Статистическая форма лица для верификации гипотезы • Пример: • Violo-Jones метод поиска лица • Violo-Jones для выделения отдельных черт – Центры глаз, уголки рта (4 точки всего) D. Cristinacce and T.F. Cootes, "Facial Feature Detection using ADABOOST with Shape Constraints", Proc.BMVC2003, Vol.1,pp.231-240
- 40. Детектор черт • Плюсвероятностная калибровка выхода классификатора для ранжирования откликов
- 41. Схема алгоритма • Идея:будем перебирать варианты положения черт лица, для каждого варианта проверяя соответствие модели формы • Схема: 1. Отсортируем отклики детекторов точек по качеству 2. Пусть i=1 3. Возьмём i самых сильных отликов для каждой точки 4. Составим список всех гипотез 5. Проверим все гипотезы 6. Если все гипотезы не удовлетворяют модели формы, тогда i=i+1 и возврат на шаг 3 7. Выберем из подходящих гипотез ту, у которой суммарный отклик черт наибольший
- 42. Модели внешности • «Appearancemodels» • Статистическая модель, кодирующая совместно форму и текстуру • Мотивация • Использование всего изображения объекта • В ASM каждая точка кодировалась независимо от остальных своим профилем T.F.Cootes, G.J. Edwards and C.J.Taylor. "Active Appearance Models", in Proc. European Conference on Computer Vision 1998 (H.Burkhardt & B. Neumann Ed.s). Vol. 2, pp. 484-498, Springer, 1998.
- 43. Построение • Строим векторформы по каждому примеру Форма x = (x1,y1, … , xn, yn)T • Строим модель x x Ps b s
- 44. Построение • Строим вектортекстуры Форма x = (x1,y1, … , xn, yn)T Текстура, g Трансформируем (warping) текстуру к усредненной форме
- 45. Преобразование текстуры Исходные точки ( xi ' , yi ' ) ( xi , yi ) • Линейная интерполяция внутри треугольников • Можно более точными методами (например, сплайны)
- 46. Построение модели • Строимвектор текстуры для каждого примера Текстура, g • Нормализуем вектора • PCA g g Pg b g
- 47. Модель текстуры 2 1 b1 2 1 2 2 b2 2 2 2 3 b3 2 3
- 48. Текстурированные модели формы • Генерируем метки • Искажаем среднюю текстуру X T ( x Psb s ) Изменение формы (текстура фиксирована)
- 49. Текстурированная модель формы 2 1 b1 2 1 2 2 b2 2 2 2 3 b3 2 3
- 50. Общая модель • Измененияформы и текстуры обычно коррелируют • При улыбке, изменяются тени (текстура) и форма • Нужно моделировать одновременно • Для каждого примера оцениваем b s , b g Wb s • Строим общий вектор, bc bg Qs • PCA b c Qc Q c g x x WPs Qs c g g Pg Q g c
- 51. Объединенная модель • Генерируемформу X и текстуру g • Искажаем текстуру так, чтобы контрольные точки совпадали с X 2 1 b1 2 1
- 52. Модель внешности лица 2 1 b1 2 1 2 2 b2 2 2
- 53. Модель внешности лица 2 3 b3 2 3 2 4 b4 2 4
- 54. Аппроксимация изображения • Еслиесть X • Находим b T • Находим c Q b • x x WPs Qs c g g Pg Q g c
- 55. Выражения лица Удивление Улыбка Нахмуриться Очки Закрыты глаза Подмигивание Подмигивание левым правым Если у нас есть разметка выражений лица, то заменив PCA на LDA можно получить «координаты», согласованные с выражением
- 56.
- 57.
- 58. Структуры мозга •72 примера • 123 точки • 5000 пикселей
- 59. Модели формы итекстуры Изменения формы (фиксированная текстура) Изменение текстуры (фиксированная форма)
- 60.
- 61. Active Appearance Models Помещаем Измеряем Уточняем модель отклонение модель Повторяем
- 62. Идея • Ошибка сопоставлениякак-то соотносится с ошибкой в параметрах • Обучим эту зависимость с помощью регрессии
- 63. Активные модели формы •Хотим найти зависимость: c AI • Схема: • Пусть имеем модель c0 • Искажаем модель: c c c0 • Генерируем g m • Извлекаем из изображения g s • Вычисляем g g s gm • Оцениваем с помощью регрессии c Ag
- 64. Насколько точно предсказание? •Предсказание x vs. истинное x
- 65. Многомасштабный подход Предсказаниеx vs. истинное x
- 66. Алгоритм AAM • ИнициализацияIm(p) • Начинаем с низкого разрешения E0 | g0 |2 • На каждом уровне • Измеряем ошибку, g g s gm • Оцениваем смещение c Ag • k=1 ci ci 1 kc • Пересчитываем ошибку, если хуже -> k=0.5, 0.25.. • Повторяем до сходимости
- 67.
- 68. Структуры мозга Начальное положение Результат
- 69.
- 70. Неудачные примеры • Плохаяинициализация -> м.б. ошибка • Используется только текущая область • Может не расшириться, как требуется
- 71.
- 72. Constrained Local Models •Прямое развитие AAM • Вместо всей текстуры – области вокруг каждой точки • Совместная вероятностная модель формы и текстуры D.Cristinacce and T.F.Cootes, "Automatic Feature Localisation with Constrained Local Models", Pattern Recognition Vol.41, No.10, pp.3054-3067, 2008
- 73.
- 74.
- 75.
- 76. Немного деталей - Правдоподобие модели текстуры - Правдоподобие модели формы R – отклик корреляции шаблона Оптимизируется с помощью симплекс-метода (Nelder-Mead)
- 77. Использование классификаторов • Заменим шаблоны на детекторы / регрессию смещения • Регрессия оценивает вектор смещения истинного положения точки от измеренного • Аналогично итерируем: • Поиск новых положений черт в окрестности текущих • Регуляризация с помощью модели формы David Cristinacce and Tim Cootes, Boosted Regression Active Shape Models, BMVC 2007
- 78. Инициализация • Средние положенияточек внутри окна, найденного методом Violo-Jones • Иллюстрированные структуры (Pictorial structures) • Которые используются и при оценке позы человека P. Felzenszwalb, D. Huttenlocher, Pictorial structures for object recognition, Int. J. Comput. Vision 61 (2005) 55–79.
- 79. Локальные детекторы • Одиндетектор на каждую точку • Обучается область нахождения каждой точки
- 80. Pictorial Tree Structure •Парные отношения между соседними точками • «Стоимость» деформации считается как отклонение от среднего расстояния между точками • Стоимость обучается по выборке
- 81.
- 82. Оптимизация • Для каждогодетектора вычисляется отклик по всему изображению • Неуверенность (uncertainty) кодируется distance transform • Отклики используются для предсказания положение родителя • Когда найден корень, процесс повторяется сверху вниз • На основе динамического программирования
- 83.
- 84. 3D модели лица • В обычных условиях лицо снимается с разных точек зрения • 2D модель не всегда может корректно учесть всё множество допустимых трансформаций • Единственный выход – учитывать 3D искажения за счёт использование 3D модели Вход Выход • Задача построение 3D модели по одному/нескольким изображениям
- 85. Постановка задачи Вход Выход • Изображение с лицом • Трёхмерная • Примерное полигональная модель положение лица лица • Должна хорошо приближать входное изображение • Параметры положения камеры относительно модели
- 86. Формальная постановка • Минимизироватьневязку • Iinput – входное изображение • Imodel – изображение (рендеринг) модели • Ω - область лица на входном изображении
- 87. Трёхмерная модель • Трёхмерная«метамодель», генерирующая полигональные модели 200 сканов Cyberware ™
- 88. Стадии работы алгоритма 1.Построение модели • по базе цветных трёхмерных сканов 2. Регулирование модели с помощью параметров 3. Подгонка модели • “Analysis by synthesis”
- 89. Пространство лиц (1) •S(a) - выпуклая комбинация полигональных моделей • Si – форма моделей из обучающей выборки • Проблема: неизвестно распределение моделей относительно параметров a
- 90. Пространство лиц (2) •Решение: применить PCA • Считаем, что формы и текстуры лиц имеют Гауссово распределение • Форма: • Текстура:
- 91. Пространство лиц (3) •Можно вычислить вероятность коэффициентов формы/текстуры: σi – стандартное отклонение i-го параметра
- 92.
- 93. Построение модели 1. Предобработка базы лазерных сканов 2. Грубое выравнивание 3. Выделение нужной области лица 4. Установление точных соответствий • Оптический поток или • Выравнивание сканов напрямую 5. PCA
- 94. Улучшения модели • Сегментированнаямодель • Линейное пространство разбивается на независимые подпространства • Сшивка
- 95. Рендеринг • Параметры модели: α – параметры формы β – параметры текстуры ρ – параметры материала, камеры, освещения, цветового баланса изображения • Модель освещения Фонга • Модель камеры • Перспективная • Слабо перспективная • Ортогональная
- 96. Атрибуты лица • Выражения лица (face expressions) • Пол • Возраст • и др. 1. Разметка параметров μi вручную 2.
- 97.
- 98.
- 99. Подгонка модели • Полныйперебор параметров невозможен (800 параметров) • Градиентный спуск • Stochastic Newton Optimization (SNO) • Inverse Image Compositional Alignment (ICIA) • По сопоставлению особенностей
- 100. Разные улучшения • Coarse-to-fineapproach • На первых итерациях оптимизируются первые 10 параметров формы и текстуры • Сначала берутся большие σI и σF • Модель разбивается на сегменты только на последних итерациях
- 101. Линейный подход • Совмещениеособенностей для инициализации модели • Вычисление камеры проекции по 2D-3D соответствиям между измеренными точками и точками средней 3D модели • Вычисление параметров модели формы через минимизацию функционала энергии (59 ключевых точек) • Извлечение текстуры из изображения на основе цветовых инвариантов • Oswald Aldrian, William A. P. Smith, A Linear Approach of 3D Face Shape and Texture Recovery using a 3D Morphable Model, 2010
- 102. Подгонка модели • Параметрыформы cs от измеренных точек y • После преобразований, получим функционал энергии E: • Моделирование 2D ошибок: • Можно свести к матричным преобразованием, с использованием SVD разложения
- 103. Геометрия • Вверху –исходные изображения • Внизу - реконструкция
- 104. Текстура Исходное Текстура • Освещение считается смесью рассеянного и диффузного (направленного) освещения • Составляется система линейных уравнений на основе модели Фонга
- 105.
- 106. Построение 3D по1 изображению
- 107.
- 108. Редактирование фотографий • Задача: • Перенести выражение лица человека с одной фотографии на другую. • Идея: • Построим 3D модели лица для обоих изображений и рассчитаем с их помощью преобразование изображений Fei Yang et.al. Expression Flow for 3D-Aware Face Component Transfer, ACM Transactions on Graphics (Proc. SIGGRAPH), 2011
- 109. Шаги • Шаг 1:вычислим с помощью ASM контуры лица на обоих изображениях • Шаг 2: вычислим 3D модель с общими параметрами личности, но разными параметрами выражения лица
- 110. Expression flow Зная соответствие3D моделей вычислим горизонтальные и вертикальные поля смещения точек лица
- 111. Процедура • (а),(c) – исходные изображения • (b),(d) – измененные по потоку выражения изображения • (e) пользовательское выделение • (f) результат
- 112. Интерактив • (а,b) уточнение разметки ASM • (d) уточнение области переноса • (e)/(f) результат без и с морщинками
- 113.
- 114.
- 115. Примеры Резульат 2D фотомонтаж без 3D уточнения
- 116.
- 117.
- 118.
- 119. Заключение • Статистические модели • Формы • Внешности • Совместные • Алгоритмы сопоставления • Активные Модели Формы (ASM) • Активные Модели Внешности (AAM) • Локальные модели с ограничениями (CLM) • Мощный инструмент интерпретации изображений