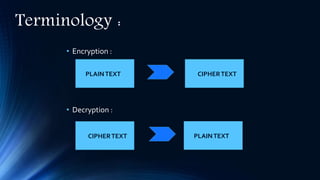
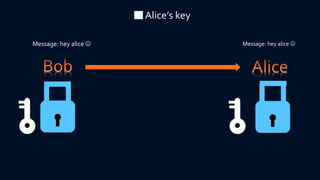
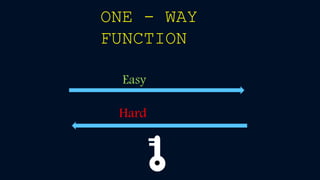
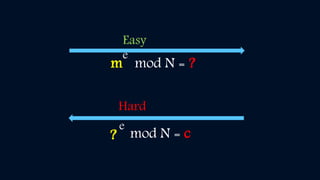
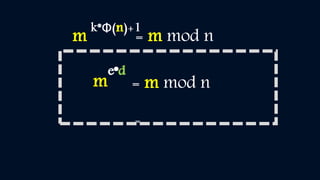
Cryptography involves encryption and decryption of messages. Encryption scrambles a message using an algorithm and key, while decryption restores the original message. There are two main types: private key cryptography uses the same key for encryption and decryption, while public key cryptography uses separate keys - a public key to encrypt and a private key to decrypt. The RSA algorithm is an example of public key cryptography that is widely used for secure communication on the internet. It relies on the fact that multiplying two large prime numbers together is easy, but factoring their product into primes is very difficult.

1. CRYPTOGRAPHY

2. Terminology :
• Encryption :
• Decryption :
PLAINTEXT CIPHERTEXT
PLAINTEXTCIPHERTEXT

3. Vernam Cipher

4. H O W A R E Y O U
7 14 22 0 17 4 24 14 20
Plain text
One time pad N C B T Z Q A R X
13 2 1 19 25 16 0 17 23
Total 20 16 23 19 42 20 24 31 43
20 16 23 19 16 20 24 5 17Subtract
U Q X T Q U Y F RCipher text

5. Private-key Cryptography :
• Same key is used to encrypt and decrypt the message
• Sender and the recipient(receiver) of the message must agree
on a common key
• It is symmetric Cryptography, parties are equal
• Hence does not protect sender from receiver forging a
message & claiming is sent by sender

6. Message: hey alice  Message: hey alice 
Alice’s key

7. Public-key Cryptography :
• Public-key cryptography involves the use of two keys:
• A Public-key, which may be known by anybody, and can
be used to encrypt messages, and verify signatures
• A Private-key, known only to the recipient(receiver), used
to decrypt messages, and sign(create) signatures

8. HelloAlice!
6EB69570
08E03CE4
Encrypt
HelloAlice! Decrypt
Public key
Private key
Bob
Alice

9. RSA Algorithm :
• RSA stands for Ron Rivest , Adi Shamir and Leonard Adleman,
who first publicly described it in 1977
• It allows anyone in the communication network to encrypt and
send message
• N=pq, where p & q are two distinct primes
• Random positive integer ‘e’ called enciphering exponent must
satisfying gcd(e, Ø(n))=1
• Pair (n,e) are made public

10. Prerequisites :
• Prime number
• Prime factorization
• Fermat’s little theorem
• Euler’s phi function
• Euler’s totient theorem

11. In 1970 british mathematician and
scientist Clifford Cocks came out with a
one way fuction called as
“The Trapdoor”

12. ONE - WAY
FUNCTION
Easy
Hard

13. For this Clifford Cocks took help of Modular Exponentiation
46 Mod 12 = 10
1
2
3
4
5
6
7
8
910
11
12
13
14
15
16
17
3 mod 17 =
12543

14. m
e
mod N = ?
Easy
Hard
e
mod N = c?

15. But what about the key
m mod N = c
e
c mod N = m
d
m mod N = m
ed

16. Prime factorization

17. 9874563210123654789302145987698745632101236547893021459876987456321012365478930214598769874563210123654789302145987698745632101236547893021459876
9874563210123654789302145987698745632101236547893021459876987456321012365478930214598769874563210123654789302145987698745632101236547893021459876
P1=
P2=
9874563210123654789302145987698745632101236547893021459876987456321012365478930214598769874563210123654789302145987698745632101236547893021459876
9874563210123654789302145987698745632101236547893021459876987456321012365478930214598769874563210123654789302145987698745632101236547893021459876
N=
N=P1×P2

18. Eulers φ function
Φ(8)=
1
2
3
4
5
6
7
8
=4

19. Φ(A)= A-1
Eg. Φ(7)=6
Where A is a prime number
Φ(A×B) = (A-1)×(B-1)
Eg. Φ(7×11) = (7-1)×(11-1)= 60

20. But the problem is
how to connect
Modular Exponentiation with
Eulers Φ Function

21. Eulers
Theorem
m = 1 mod n
Φ(n)

22. Lets make some modifications in the Eulers theorem
m = 1 mod n
Φ(n)
1 =1
k
m = 1 mod n
k×Φ(n)
1×m=m m×m = m mod n
k×Φ(n)
m = m mod n
k×Φ(n)+1

23. m = m mod n
k*Φ(n)+1
m = m mod n
e*d
k*Φ(n)+1
e*d
=

25. T H
U