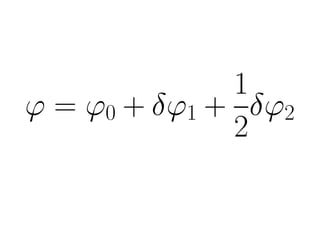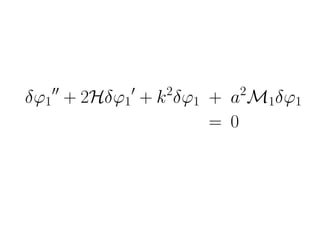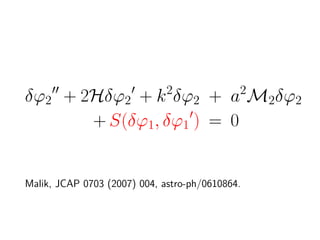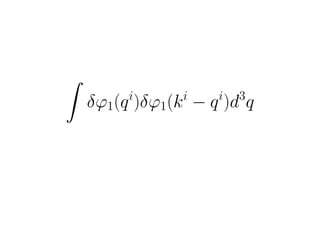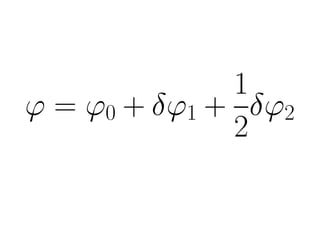
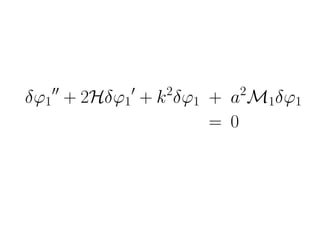
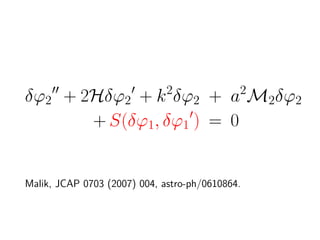
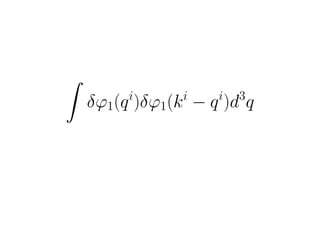
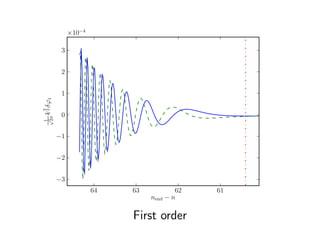
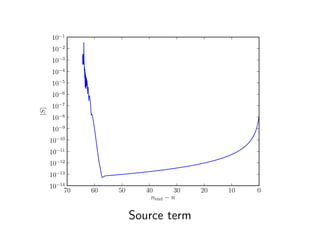
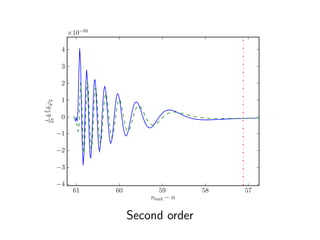
This document discusses numerical calculations of second-order perturbations in cosmological perturbations. It presents equations for the first-order and second-order perturbations δφ1 and δφ2 of a field φ, including a source term S(δφ1, δφ1) coupling the first-order perturbations. Graphs show results for the first-order perturbation √k2δφ1/3 and second-order perturbation k2δφ2/3 from a code implementing these calculations. Future work is needed to go beyond first order, include convolution, and consider multiple fields.

1. Numerical calculation of second
order perturbations
Ian Huston
Astronomy Unit, Queen Mary, University of London
arXiv: 0907.2917
with Karim Malik, accepted by JCAP

2. 1
ϕ = ϕ0 + δϕ1 + δϕ2
2

3. δϕ1 + 2Hδϕ1 + k 2δϕ1 + a2M1δϕ1
= 0

4. δϕ2 + 2Hδϕ2 + k 2δϕ2 + a2M2δϕ2
+ S(δϕ1, δϕ1 ) = 0
Malik, JCAP 0703 (2007) 004, astro-ph/0610864.

5. δϕ1(q i)δϕ1(k i − q i)d3q

6. code():
Following Salopek et al. (1989), Martin & Ringeval (2006)

7. ×10−4
3
2
1
√1 k 2 δϕ1
3
0
2π
−1
−2
−3
64 63 62 61
nend − n
First order

8. 10−1
10−2
10−3
10−4
10−5
10−6
10−7
|S|
10−8
10−9
10−10
10−11
10−12
10−13
10−14
70 60 50 40 30 20 10 0
nend − n
Source term

9. ×10−93
4
3
2
1
k 2 δϕ2
1 3
0
2π
−1
−2
−3
−4
61 60 59 58 57
nend − n
Second order

10. v1.0:
1000+ k modes
Slow roll source term
Parallelisable

11. Need to go beyond 1st order
Convolution required
Next steps: full eqn, multi-field
arXiv: 0907.2917