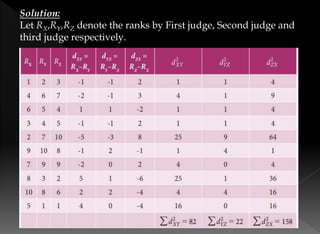
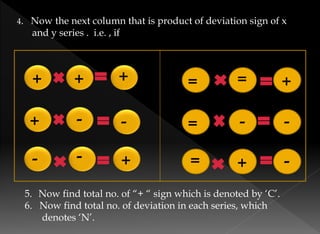
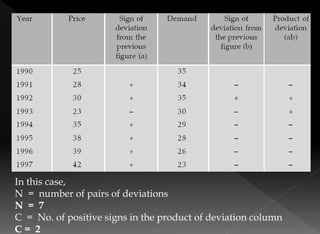
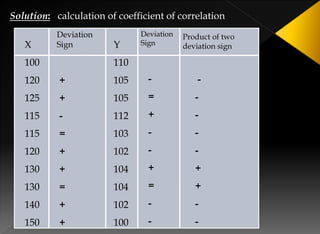
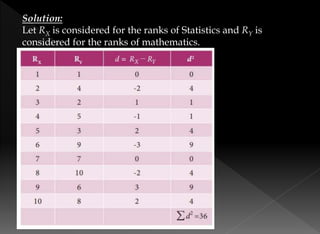
The document details the rank correlation method developed by Edward Spearman, used for qualitative data that cannot be quantified but can be ranked. It explains formulas for calculating rank correlation coefficients, addressing tied observations, and provides examples involving students' ranks across tests and rankings in competitions. Additionally, it describes the method of concurrent deviations for analyzing relationships between two variables.

2.  When qualitative facts cannot be expressed in
numbers easily but can only be assessed
qualitatively they may be placed on the basis of
their ranks and in such case this method is used.
 For eg. Beauty cannot be expressed in numbers but
can be arranged by giving them respective ranks .

3. This method was developed by Edward Spearman.
This method can only be used in individual series.
r= 1- 6 ∑d2 r= 1- 6 ∑d2
N3-N OR N(N2-1)
where
d = The difference of two ranks = R X - RY and
N = Number of paired observations.
Rank coefficient of correlation value lies between –1 and +1.
Symbolically, –1≤r≤+1

4. 1. Apply ranks to the variables of the series separately.
2. Rank can be given in ascending or descending order i.e. either
giving biggest variable rank 1 or giving smallest variable rank 1.
3. If the variables in a series are equal then they will be treated as
follows –
suppose if 3rd, 4th, 5th values are equal their given rank will be
3+4+5 = 4th rank, and just the nest value will be given 6thrank.
3
4. Now we have to calculate deviations. They are called rank
differences i.e. (d) , total of d i.e. Σd will always be equals to 0.
5. Each difference is squared up i.e. d2 . Then we apply the
formula
r= 1- 6 ∑d2
N3-N
where N= number of pairs of values

5. When two or more value in either or both the series are equal,
following correction factor also applies-
{1/12(m3-m)+……}
This correlation is applied as many times as the value are equal in
both the series taken together.
‘m’ represents the number of equal value.
For eg. 40 has been repeated 2 times and 45 has been repeated 4
times , so the value of m for 40 is 2 and value of m for 45 is 4.
The formula along with this correlation is –
6 [ ∑d2 +1/12(m3-m)+ 1/12(m3-m) …… ]
r = 1 –
N3-N

6. 1. The following are the ranks obtained by 10 students in
Statistics and Mathematics
Find the rank correlation coefficient.

7. Solution:
Let RX is considered for the ranks of Statistics and RY is
considered for the ranks of mathematics.

8. r= 1 - 6 ∑d2
N3-N
Where N = no. of pairs if value
r = 1- 6*36
1000-10
= 1- 216
9990
= 1- 0.218
r = +0.782

9. 2. Rank Correlation for tied observations. Following are the
marks obtained by 10 students in a class in two tests.
Students A B C D E F G H I J
Test 1 70 68 67 55 60 60 75 63 60 72
Test 2 65 65 80 60 68 58 75 63 60 70
Calculate the rank correlation coefficient between the marks of
two tests.
Students A B C D E F G H I J
Test 1 70 68 67 55 60 60 75 63 60 72
Test 2 65 65 80 60 68 58 75 63 60 70

10. Student Test 1 R1 Test 2 R2 D D2
A 70 3 65 5.5 - 2.5 6.25
B 68 4 65 5.5 -1.5 2.25
C 67 5 80 1.0 4.0 16.00
D 55 10 60 8.5 1.5 2.25
E 60 8 68 4.0 4.0 16.00
F 60 8 58 10.0 -2.0 4.00
G 75 1 75 2.0 -1.0 1.00
H 63 6 62 7.0 -1.0 1.00
I 60 8 60 8.5 0.5 0.25
J 72 2 70 3.0 -1.0 1.00
total ∑D2=50.00
Solution-
Student Test 1 R1 Test 2 R2 D D2
A 70 3 65 5.5 - 2.5 6.25
B 68 4 65 5.5 -1.5 2.25
C 67 5 80 1.0 4.0 16.00
D 55 10 60 8.5 1.5 2.25
E 60 8 68 4.0 4.0 16.00
F 60 8 58 10.0 -2.0 4.00
G 75 1 75 2.0 -1.0 1.00
H 63 6 62 7.0 -1.0 1.00
I 60 8 60 8.5 0.5 0.25
J 72 2 70 3.0 -1.0 1.00
total ∑D2=50.00

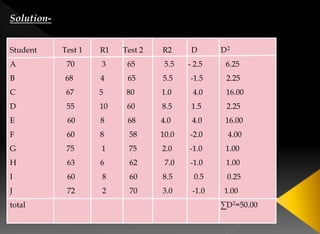
11. 60 is repeated 3 times in test 1
60, 65 is repeated twice in test 2
m=3; m=2; m=2
r = 1 – 6 [ ∑d2 +1/12(m3-m)+ 1/12(m3-m) …… ]
N3-N
r = 1- 6 [50+1/12(33-3)+1/12(23-2)+1/12(23-2)]
1000-10
r = 1- 6 [50+1/12(27-3)+1/12(8-2)+1/12(8-2)]
990
r = 1- 6 [50+1/12*24+1/12*6+1/12*6]
990
r = 1- 6(50+2+1/2+1/2)
990

12. r = 1- 6*53
990
r = 1- 672/990
r = 1- 0.678
r = +0.322

13. 3. Ten competitors in a beauty contest are ranked by three
judges in the following order
Use the method of rank correlation coefficient to determine
which pair of judges has the nearest approach to common
taste in beauty?

14. Solution:
Let RX,RY,RZ denote the ranks by First judge, Second judge and
third judge respectively.

15. r xy = 1- 6 ∑ d2
xy
N3-N
= 1- 6(82)
1000-10
= 1- 0.4969
= +0.5031
r yz = 1- 6 ∑ d2
yz
N3-N
= 1- 6(22)
1000-10
= 1- 132/990
= 1- 0.133
= +0.8667

16. r ZX = 1- 6 ∑ d2
ZX
N3-N
= 1- 6(158)
1000-10
= 1- 948/990
= 1- 0.9576
= +0.0424
Since the rank correlation coefficient between Second and
Third judges i.e., rYZ is positive and is nearest to “+1” among
the three coefficients. So, Second judge and Third judge have
the nearest approach for common taste in beauty.

17.  This method is used where the object is just to know in
which direction the correlation is present in two series –
positive or negative.
 This method involves in attaching a positive sign for a x-
value (except the first) if this value is more than the
previous value and assigning a negative value if this value is
less than the previous value.
 This is done for the y-series as well. The deviation in the x-
value and the corresponding y-value is known to be
concurrent if both the deviations have the same sign.

18.  Denoting the number of concurrent deviation by c and total
number of deviations as N (which must be one less than the
number of pairs of x and y values), the coefficient of
concurrent-deviations is given by-
r = ± ± 2C-N
N
Where C= total no. of positive signs
N= total no. of signs

19. 1. Take x series compare it s second value from the first
value , if second value is bigger put + sign against
second and if second value is smaller put – sign
against second value i.e.
• if succeeding value is more put ‘’ + ‘’ sign
• if preceding value is more put “ – “ sign
repeat this for all the value of x series and do the
same for y series.
we will se that if pairs are 10 then sign will be 9 in
each series i.e. first left blank.
2. If both the values in sequence are equal put = sign
against the second one.
3. Only algebric signs are put not the figure of
difference.

20. 4. Now the next column that is product of deviation sign of x
and y series . i.e. , if
5. Now find total no. of “+ “ sign which is denoted by ‘C’.
6. Now find total no. of deviation in each series, which
denotes ‘N’.
+ + +
+ -
- -
-
+
= =
=
=
-
+
+
-
-

21. 7. Now using the formula-
r = ± ± 2C-N
N
8. If (2c–m) > 0, then we take the positive sign both inside and
outside the radical sign and if (2c–m) < 0, we are to consider
the negative sign both inside and outside the radical sign.
the coefficient of concurrent- deviations also lies between –1
and 1, both inclusive.
That is,
-1 ≤ r ≤ 1

22. 1. Find the coefficient of concurrent deviation from the
following data.
Solution :
Computation of Coefficient of Concurrent-Deviations.

23. In this case,
N = number of pairs of deviations
N = 7
C = No. of positive signs in the product of deviation column
C = 2

24. r = ± ± 2C-N
N
= ± ± (4-7)
7
= - - (-3)
7
= - (3/7)
= - 0.65

25. 2. From the following data calculate coefficient of correlation
by concurrent deviation method:
x 100 120 125 115 115 120 130 130 140 150
Y 110 105 105 112 103 102 104 104 102 100

26. Solution: calculation of coefficient of correlation
X
100
120
125
115
115
120
130
130
140
150
+
+
-
=
+
+
=
+
+
Deviation
Sign Y
110
105
105
112
103
102
104
104
102
100
-
=
+
-
-
+
=
-
-
Deviation
Sign
Product of two
deviation sign
-
-
-
-
-
+
+
-
-

27. In this case,
N = number of pairs of deviations
N = 9
C = No. of positive signs in the product of deviation
column
C = 2
r = ± ± (2C-N)
N
= - - (4-9)
9
= - - ( -5/9)
= - (5/9)
= - 0.5556
= -0.745
Therefore X and Y have negative
correlation.