The document summarizes a lecture on cooperative game theory under interval uncertainty given at the 6th Summer School AACIMP in Kyiv, Ukraine from August 8-20, 2011. The lecture introduced cooperative interval games where payoffs are uncertain and defined as intervals rather than single values. It defined concepts such as the core set and imputation set for interval games, and showed that a game has a non-empty core if and only if it is strongly balanced. The lecture also discussed two-person interval games and economic applications of interval game theory.











![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
Cooperative games under interval uncertainty
Cooperative games under interval uncertainty
A cooperative n-person interval game in coalitional form is an
ordered pair < N, w >:
N := {1, 2, . . . , n} is the set of players
w : 2N → I (R) is the characteristic function which assigns to
each coalition S ∈ 2N a closed interval w (S) ∈ I (R)
I (R) is the set of all closed intervals in R such that
w (∅) = [0, 0]
The worth interval w (S) is denoted by [w (S), w (S)].
Here, w (S) is the lower bound and w (S) is the upper bound.
If all the worth intervals are degenerate intervals, i.e.,
w (S) = w (S), then the interval game < N, w > corresponds to
the classical cooperative game < N, v >, where v (S) = w (S).](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-12-320.jpg)



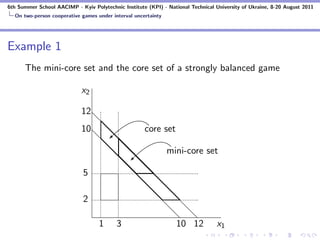
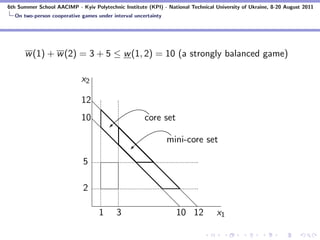
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
On two-person cooperative games under interval uncertainty
Balancedness and related topics
s1 ∈ w (1) = [w (1), w (1)], s2 ∈ w (2) = [w (2), w (2)]
t ∈ w (1, 2) = [w (1, 2), w (1, 2)]
w s1 ,s2 ,t : the selection of w corresponding to s1 , s2 and t
C (w ) = ∪ C (w s1 ,s2 ,t )|(s1 , s2 , t) ∈ w (1) × w (2) × w (1, 2)
MC (w ) = ∪ C (w s1 ,s2 ,t )|s1 ∈ [w (1), w (1)], s2 ∈ [w (2), w (2)]
MC (w ) ⊂ ∪ C (w s1 ,s2 ,t )|s1 ∈ w (1), s2 ∈ w (2), t ∈ w (1, 2)
The mini-core set is interesting because for each s1 , s2 and t all
points in MC (w ) with x1 + x2 = t are also in C (w s1 ,s2 ,t ).](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-18-320.jpg)


![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
On two-person cooperative games under interval uncertainty
ψ α -values and their axiomatization
α = (α1 , α2 ) ∈ [0, 1] × [0, 1]: the optimism vector
α
s1 1 (w ) := α1 w (1) + (1 − α1 )w (1)
α
s2 2 (w ) := α2 w (2) + (1 − α2 )w (2)](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-21-320.jpg)

![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
On two-person cooperative games under interval uncertainty
A map F : IG {1,2} → K(R2 ) assigning to each interval game w
a unique curve
F (w ) : [w (1, 2), w (1, 2)] → R2
for t ∈ [w (1, 2), w (1, 2)], i ∈ {1, 2}, in K(R2 ) is called a solution.
IG {1,2} : the family of all interval games with player set {1, 2}](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-23-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
On two-person cooperative games under interval uncertainty
F has the following properties:
(i) efficiency (EFF), if for all w ∈ IG {1,2} and
t ∈ [w (1, 2), w (1, 2)]; i∈N F (w )(t)i = t.
(ii) α-symmetry (α-SYM), if for all w ∈ IG {1,2} and
α α
t ∈ [w (1, 2), w (1, 2)] with s1 1 (w ) = s2 2 (w );
F (w )(t)1 = F (w )(t)2 .
(iii) covariance with respect to translations (COV), if for all
w ∈ IG {1,2} , t ∈ [w (1, 2), w (1, 2)] and a = (a1 , a2 ) ∈ R2
F (w + ˆ)(a1 + a2 + t) = F (w )(t) + a.
a](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-24-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
On two-person cooperative games under interval uncertainty
ψ α -values and their axiomatization
ˆ ∈ IG {1,2} is defined by
a
ˆ({1}) = [a1 , a1 ], ˆ({2}) = [a2 , a2 ]
a a
ˆ({1, 2}) = [a1 + a2 , a1 + a2 ]
a
w + ˆ ∈ IG {1,2} is defined by
a
(w + ˆ)(s) = w (s) + ˆ(s)
a a
for
s ∈ {{1} , {2} , {1, 2}}](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-25-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
On two-person cooperative games under interval uncertainty
For each w ∈ IG {1,2} and t ∈ [w (1, 2), w (1, 2)]
we define the map
ψ α : IG {1,2} → K(R2 )
such that
α α
ψ α (w )(t) := (s1 1 (w ) + β, s2 2 (w ) + β),
where
1 α α
β = (t − s1 1 (w ) − s2 2 (w )).
2](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-26-320.jpg)



![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
On two-person cooperative games under interval uncertainty
Marginal curves and the Shapley-like solution
The marginal curves for a two-person game < N, w > are defined
by
mσ,α (w ) : [w (1, 2), w (1, 2)] → R2 ,
where
α α
m(1,2),α (w )(t) = (s1 1 (w ), t − s1 1 (w )),
α α
m(2,1),α (w )(t) = (t − s2 2 (w ), s2 2 (w )).
The Shapley-like solution ψ α is equal to
1
ψ α (w ) = (m(1,2),α (w ) + m(2,1),α (w )).
2](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-30-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
Some economic examples
Example 2
A bankruptcy situation with two claimants with demands d1 = 70
and d2 = 90 on (uncertain) estate E = [100, 120].
w (∅) = [0, 0], w (1) = [(E − d2 )+ , (E − d2 )+ ] = [10, 30]
w (2) = [(E − d1 )+ , (E − d1 )+ ] = [30, 50], w (1, 2) = [100, 120].
w (1) + w (2) = 30 + 50 ≤ w (1, 2) = 100
(a strongly balanced game)](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-31-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
Some economic examples
1
ψ (0,0) (w )(t) = (10 + β, 30 + β) with β = (t − 40) and t ∈ [100, 120]
2
t 100 106 110 114 120
β 30 33 35 37 40
ψ (0,0) (w )(t) (40, 60) (43, 63) (45, 65) (47, 67) (50, 70)](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-32-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
Some economic examples
The mini-core set and the ψ (0,0) -values of the game < N, w >,
where L = {ψ α (w )(t)|t ∈ [100, 120]}.
x2
120
d
100 d
d d
d d
d Ld
d d mini-core
50 d ©d
d d
30 d d
d d
d d
d d
10 30 100 120 x1](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-33-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
Some economic examples
Example 3
A reward game with N = {1, 2} which is not strongly balanced.
w (∅) = [0, 0], w (1) = [1, 3], w (2) = [2, 5], w (1, 2) = [6, 10].
ψ (0,0) (w )(t) = (1 + β, 2 + β) with 3 + 2β = t and t ∈ [6, 10].
t 6 7 8 9 10
β 11 2 2 21 2 3 31 2
(0,0) (w )(t) 1 1 1 1 1 1
ψ (2 2 , 3 2 ) (3, 4) (3 2 , 4 2 ) (4, 5) (4 2 , 5 2 )](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-34-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
Some economic examples
x2
10
d
d
d
6 d
© mini-core
5 d d
d d
dL
d
2 d d
d d
d d
1 3 6 10 x1
The mini-core set and the ψ α -values of an interval game, where
L = {ψ α (w )(t)|t ∈ [6, 10]}.](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-35-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
References
References
[1] Alparslan G¨k S.Z., Miquel S. and Tijs S., “Cooperation under
o
interval uncertainty”, Mathematical Methods of Operations
Research, Vol. 69 (2009) 99-109.
[2] Bondareva O.N., “Certain applications of the methods of linear
programming to the theory of cooperative games”, Problemly
Kibernetiki 10 (1963) 119-139 (in Russian).
[3] Branzei R., Dimitrov D. and Tijs S., “Models in Cooperative
Game Theory”, Springer-Verlag Berlin (2008).
[4] Gillies D.B., “Some Theorems on n-person Games”, Ph.D.
Thesis, Princeton University Press (1953).](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-36-320.jpg)
![6th Summer School AACIMP - Kyiv Polytechnic Institute (KPI) - National Technical University of Ukraine, 8-20 August 2011
References
[5] Shapley L.S., “A value for n-person games”, Annals of
Mathematics Studies 28 (1953) 307-317.
[6] Shapley L.S., “On balanced sets and cores”, Naval Research
Logistics Quarterly 14 (1967) 453-460.
[7] Tijs S., “Introduction to Game Theory”, SIAM, Hindustan
Book Agency, India (2003).](https://image.slidesharecdn.com/lecture3-110909120348-phpapp02/85/Cooperation-under-Interval-Uncertainty-37-320.jpg)