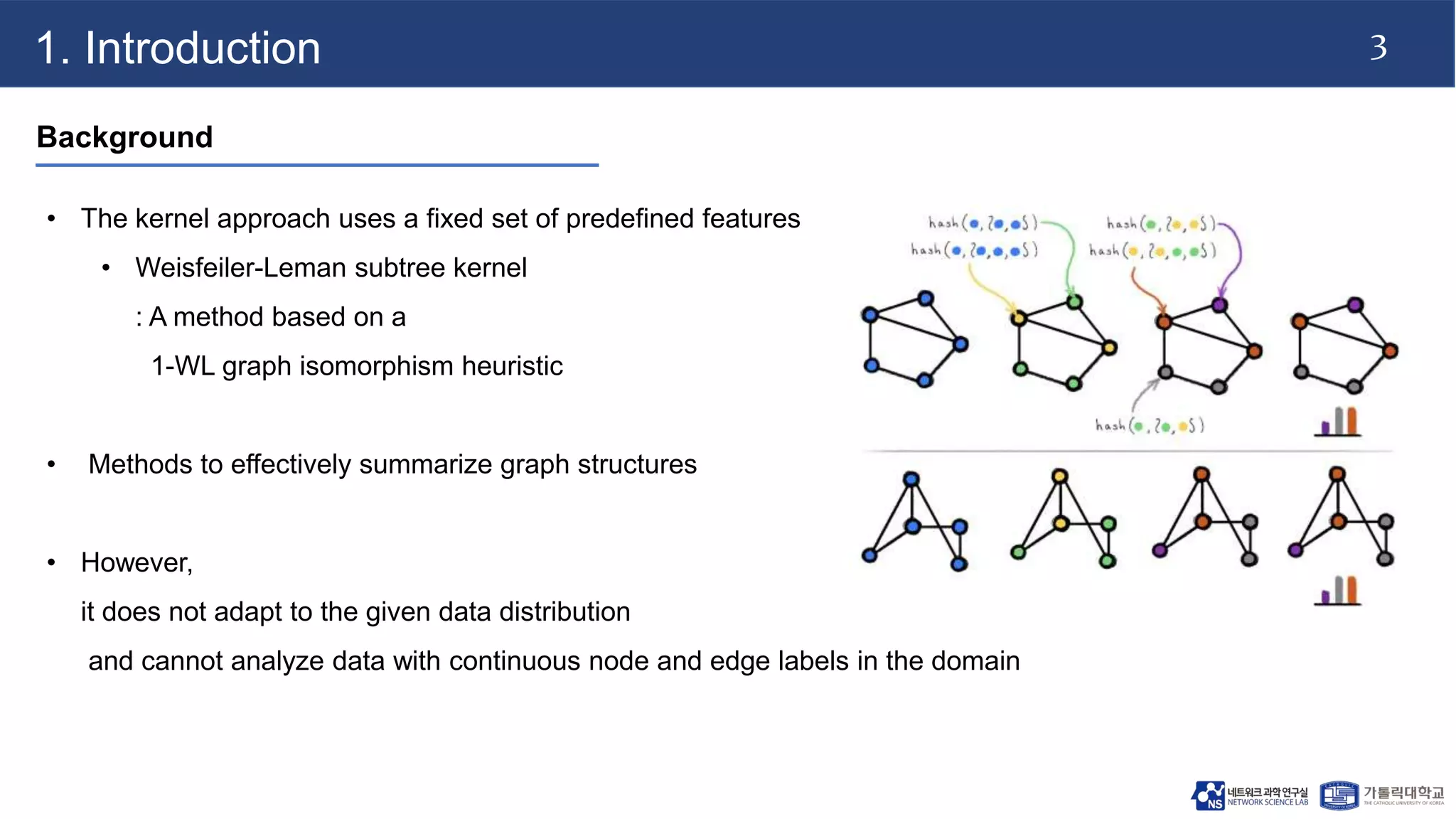
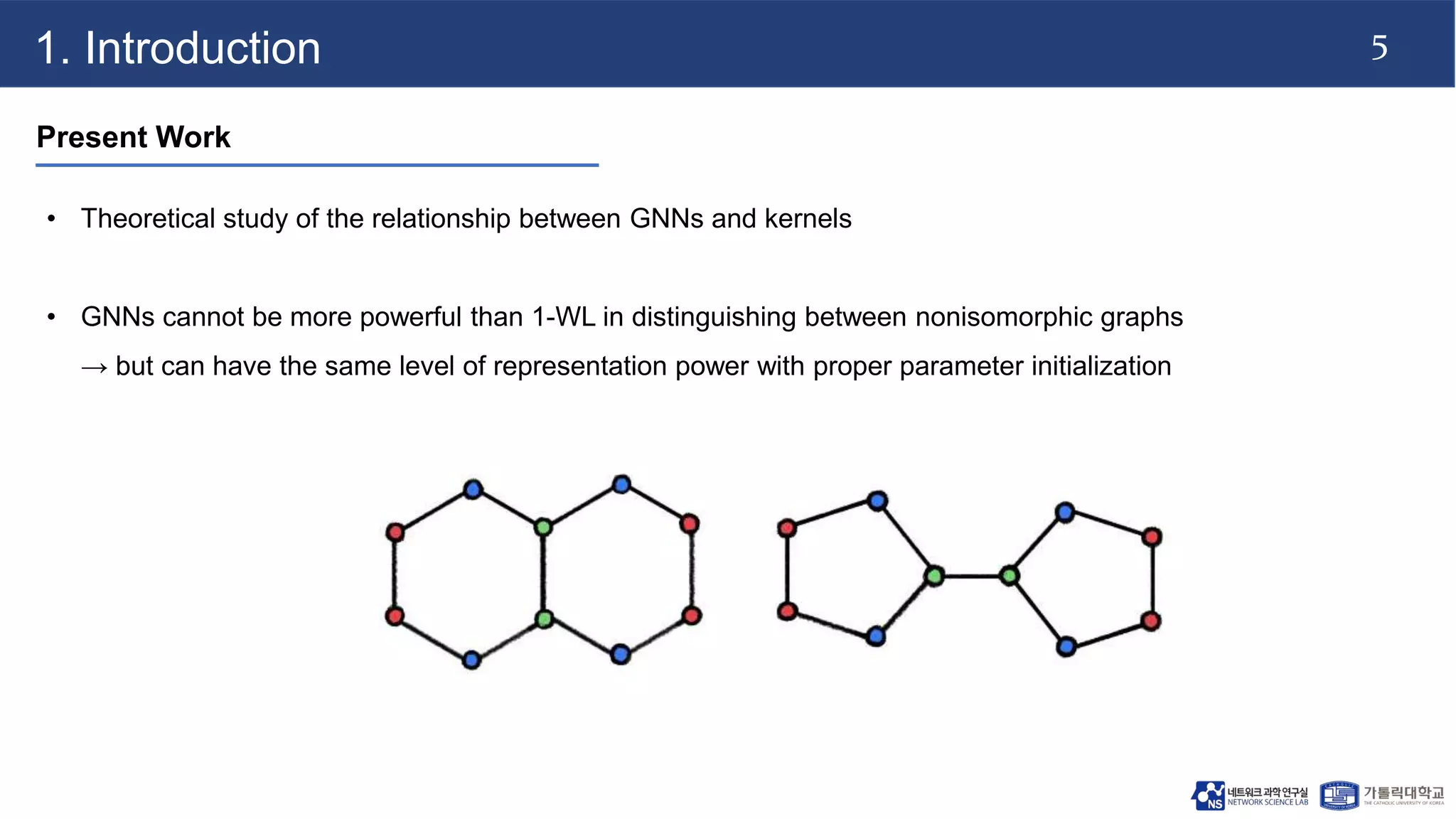
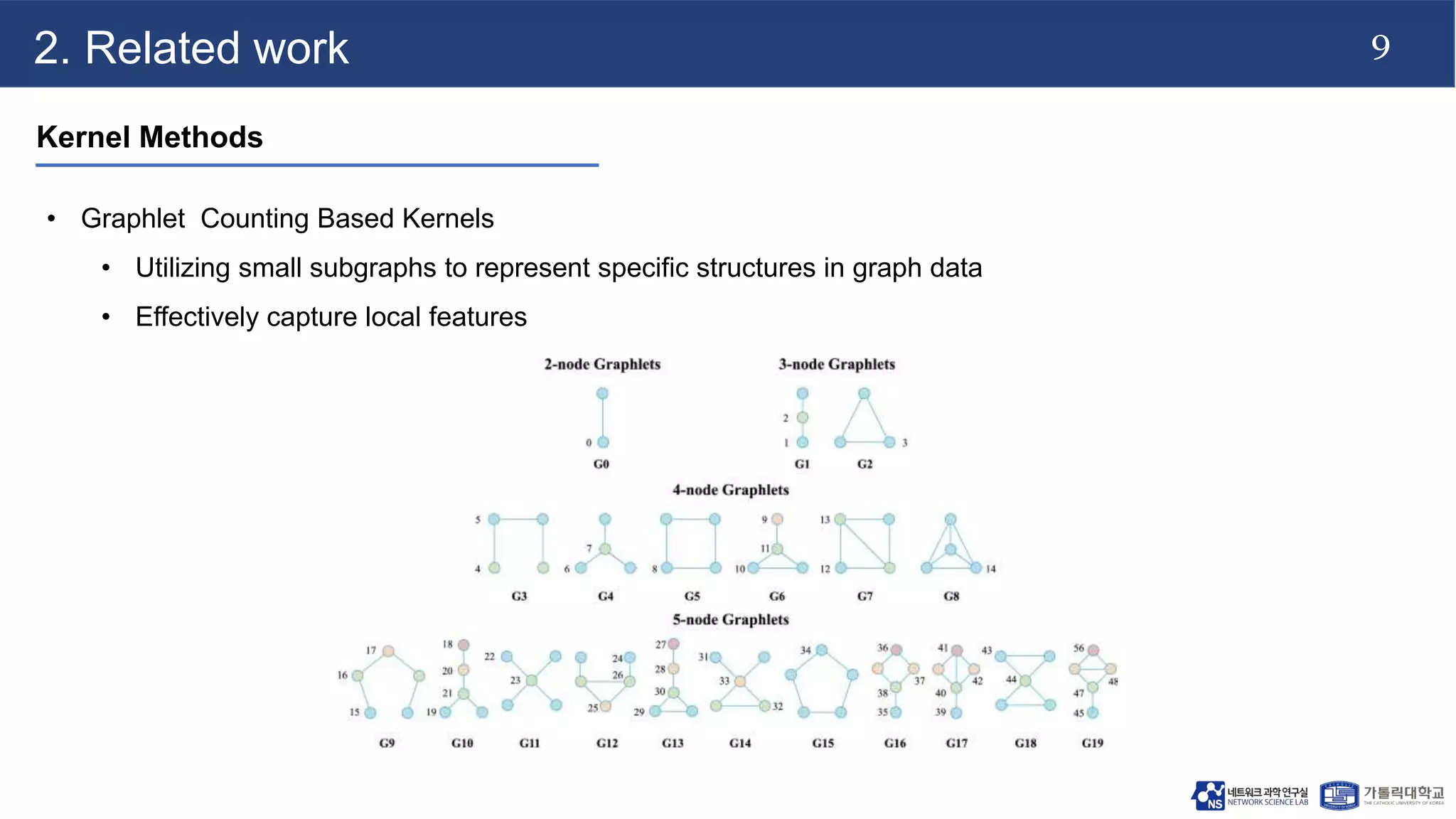
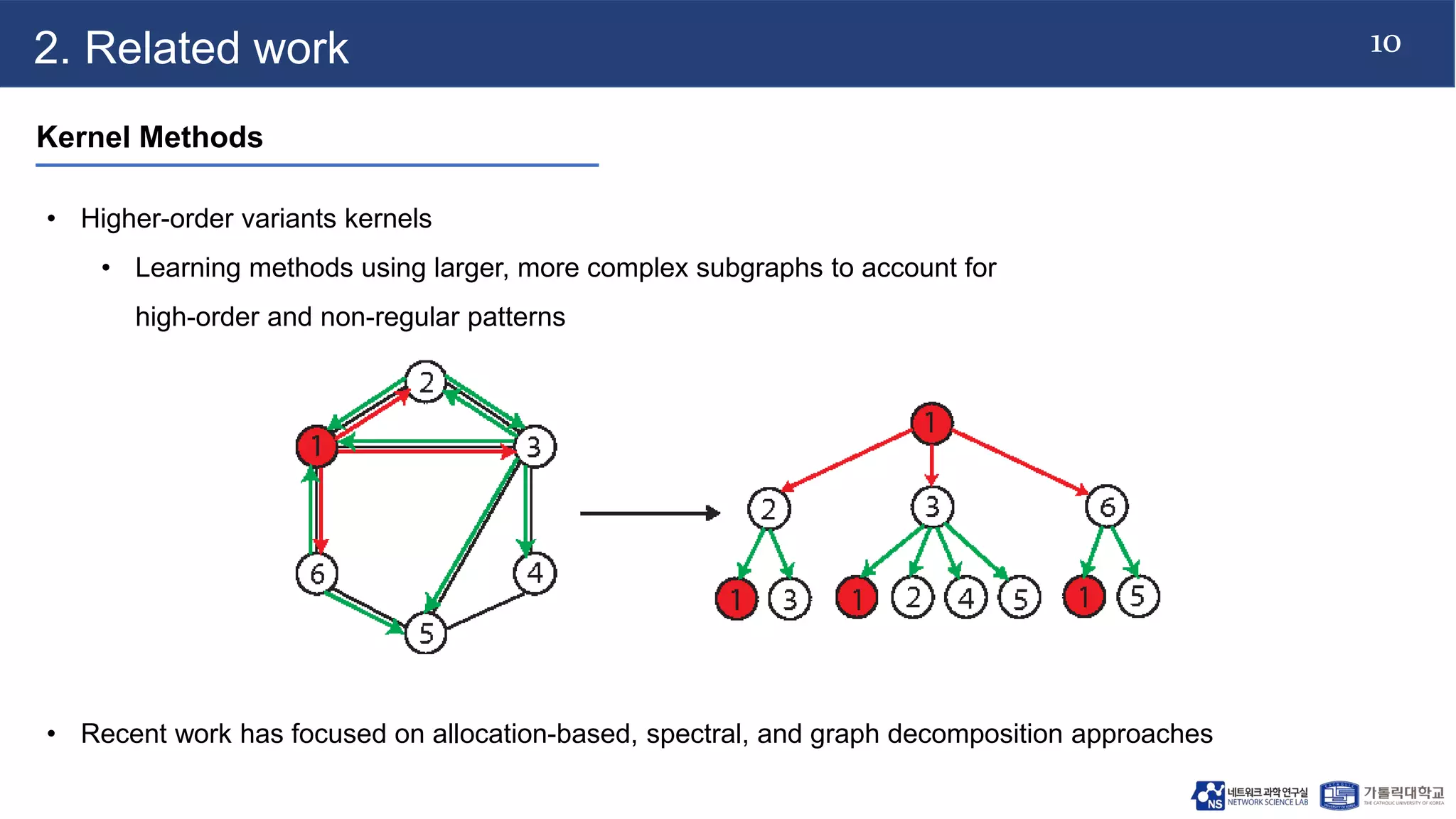
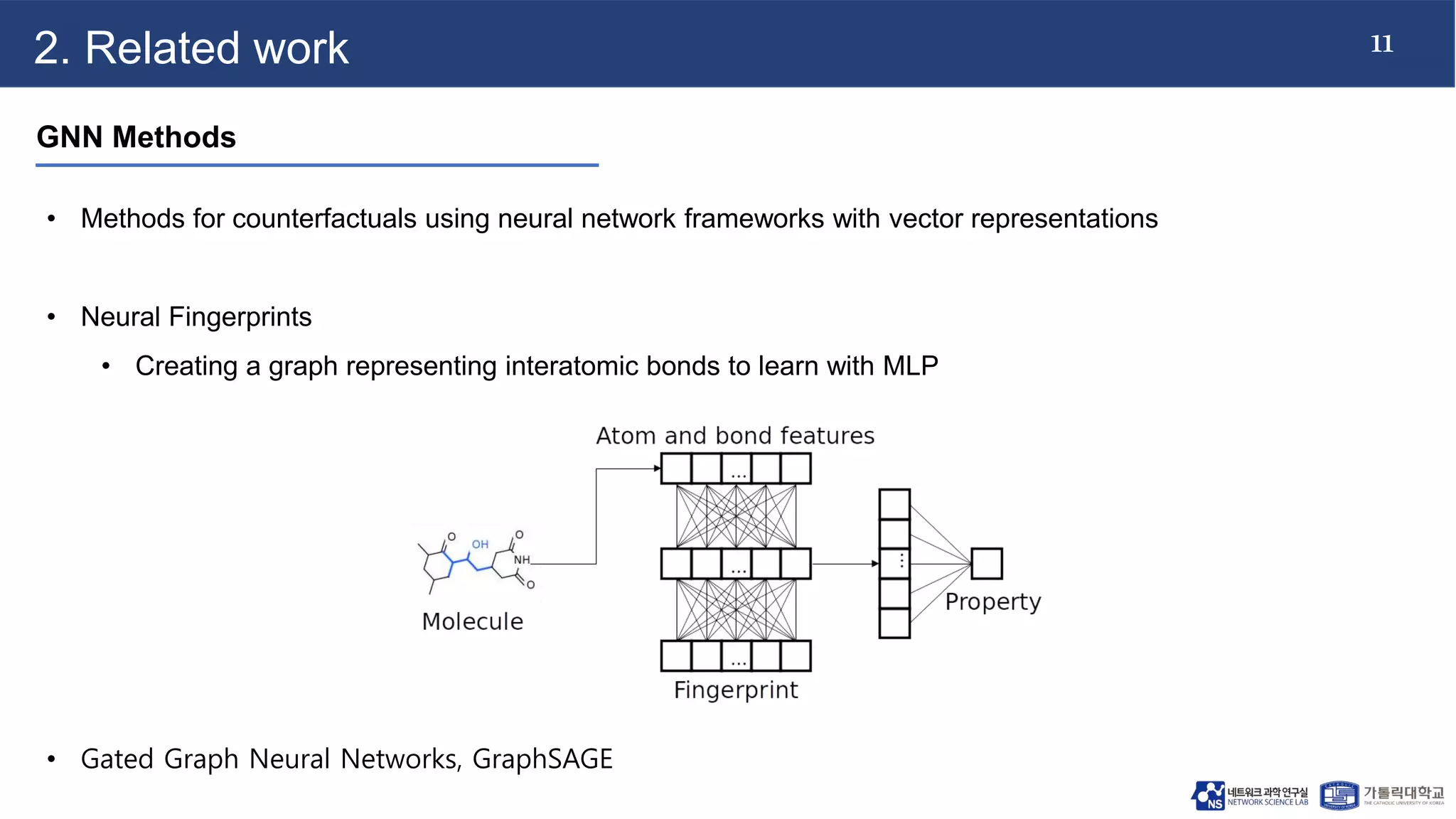
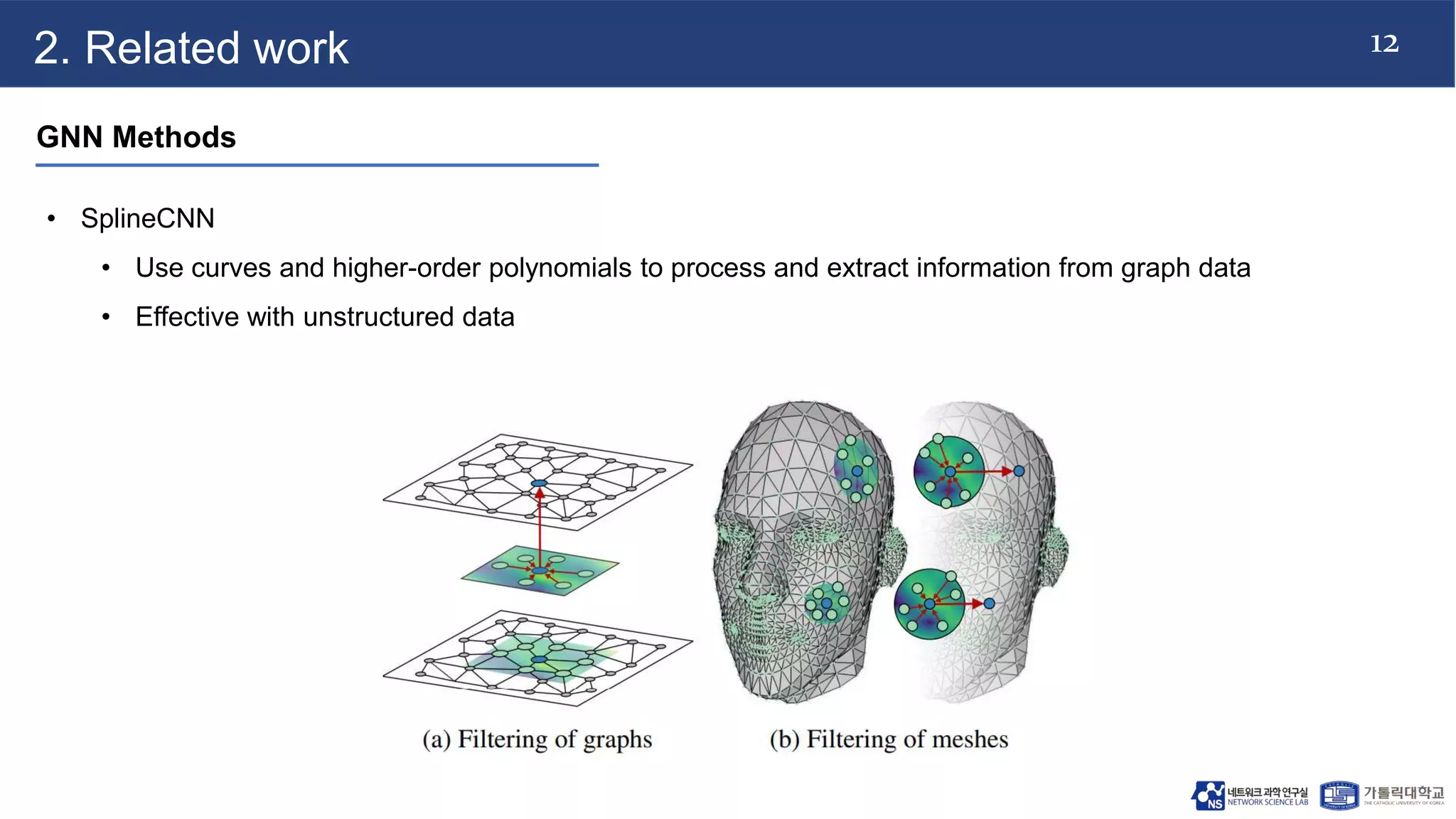
The document discusses advancements in machine learning techniques for analyzing graph structures, highlighting the limitations of kernel methods and the advantages of graph neural networks (GNNs). It proposes a novel model called k-GNN, which incorporates theoretical insights to enable direct message passing between subgraph structures, while maintaining comparable representational power to the Weisfeiler-Lehman algorithm. The work emphasizes the importance of higher-order graph characterization in classification and regression tasks.

1. Hyo Eun Lee
Network Science Lab
Dept. of Biotechnology
The Catholic University of Korea
E-mail: gydnsml@gmail.com
2023.09.04
AAAI 2019

2. 1
 Introduction
• Background
• Present Work
• Propose
 Related work
• Kernel Methods
• GNN Methods

3. 2
1. Introduction
Background
• Graph structures are used in a variety of domains and applications
• Thus, it is important to develop machine learning techniques
that can utilize the information embedded in the graph structure and feature information of nodes and edges
• Recently, methods using graph kernel-based and graph neural network algorithms were proposed

4. 3
1. Introduction
Background
• The kernel approach uses a fixed set of predefined features
• Weisfeiler-Leman subtree kernel
: A method based on a
1-WL graph isomorphism heuristic
• Methods to effectively summarize graph structures
• However,
it does not adapt to the given data distribution
and cannot analyze data with continuous node and edge labels in the domain

5. 4
1. Introduction
Background
• Graph neural network methods solve the limitations of graph kernel methods
using a machine learning framework
• Aggregate using a neural network with node neighbors using feature vectors
• A method that neuralizes the 1-WL algorithm
• GNN framework has the characteristics of message passing in terms of aggregating and forwarding local
neighborhood information.
• So it can be trained in an end-to-end method, allowing for adaptability and better generalization

6. 5
1. Introduction
Present Work
• Theoretical study of the relationship between GNNs and kernels
• GNNs cannot be more powerful than 1-WL in distinguishing between nonisomorphic graphs
→ but can have the same level of representation power with proper parameter initialization

7. 6
1. Introduction
Propose
• Propose K-GNN, a generalized version of GNN based on theoretical relationships
• Based on the K- WL algorithm for neural architectures
• Performs direct message passing between subgraph structures (rather than nodes individually)

8. 7
1. Introduction
Summary
• Show that GNNs cannot be more powerful than 1-WL in distinguishing between isomorphic (sub)graphs
(which was not clear in theory)
, and that GNNs have the same ability as 1-WL, assuming proper parameter initialization
• Propose k-GNNs and "1-k-GNNs", a hierarchical version of k-GNNs
, a model that can capture the fine and continuous structure of graphs and the relationship
• Experimentally prove
that higher-order graph characterization is important for graph classification and regression tasks

9. 8
2. Related work
Kernel Methods
• Mapping a Graph to Hilbert Space
• One of the most common methods used in supervised learning
• Important early research: random walk-based kernels, shortest path-based kernels
• Recent research focuses on scalability and avoiding gram matrix computation

10. 9
2. Related work
Kernel Methods
• Graphlet Counting Based Kernels
• Utilizing small subgraphs to represent specific structures in graph data
• Effectively capture local features

11. 10
2. Related work
Kernel Methods
• Higher-order variants kernels
• Learning methods using larger, more complex subgraphs to account for
high-order and non-regular patterns
• Recent work has focused on allocation-based, spectral, and graph decomposition approaches

12. 11
2. Related work
GNN Methods
• Methods for counterfactuals using neural network frameworks with vector representations
• Neural Fingerprints
• Creating a graph representing interatomic bonds to learn with MLP
• Gated Graph Neural Networks, GraphSAGE

13. 12
2. Related work
GNN Methods
• SplineCNN
• Use curves and higher-order polynomials to process and extract information from graph data
• Effective with unstructured data