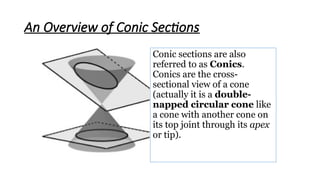
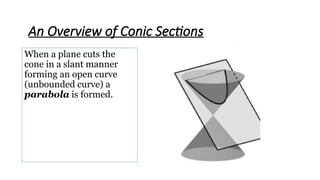
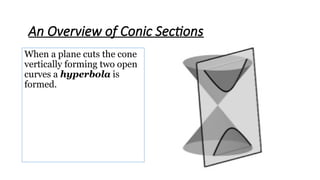
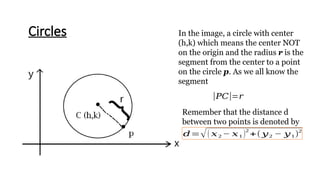
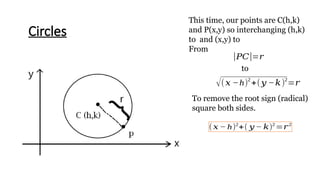
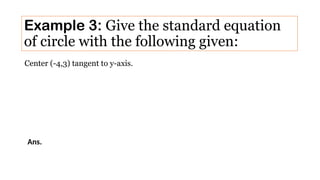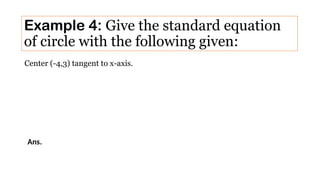Chapter 1 introduces conic sections, including circles, parabolas, ellipses, and hyperbolas, explaining how they are formed by intersecting a cone with a plane. It defines a circle as the locus of points equidistant from a center and provides the standard form of a circle's equation along with examples for practice. The chapter concludes with methods to determine the center and radius of a circle from its general equation.

1. Chapter 1 – Analytic
Geometry
Lesson 1 - The Conic sections & Circles: An
Introduction
PRE-CALCULUS
PREPARED BY: SIR REYMART SALADAS

2. Learning Objectives
At the end of the lesson, the student should be able to:
a. Illustrate the different types of conic sections: parabola,
ellipse, circle, hyperbola, and degenerate cases
b. Define a circle
c. Determine the equation of circle in standard form; and
d. Sketch a circle in a rectangular coordinate system.

3. *Interaction Part: Conics (if possible)

4. An Overview of Conic Sections
Conic sections are also
referred to as Conics.
Conics are the cross-
sectional view of a cone
(actually it is a double-
napped circular cone like
a cone with another cone on
its top joint through its apex
or tip).

5. When a plane cuts the cone
horizontally a circle is formed. As
shown in the image on the right the
lower portion depicts a circle. On
the other hand, when a plane cuts
the cone in a slant manner forming
a closed curve (bounded curve) an
ellipse is formed.
An Overview of Conic Sections

6. When a plane cuts the
cone in a slant manner
forming an open curve
(unbounded curve) a
parabola is formed.
An Overview of Conic Sections

7. When a plane cuts the cone
vertically forming two open
curves a hyperbola is
formed.
An Overview of Conic Sections

8. If you take a close look of the conics formed, its edges
(technically, it is called the cross-sectional area) formed would
look like this:
An Overview of Conic Sections
It's just like a
doodle but on the
next lessons and
chapter you will be
fascinated how
these doodles will
doodle your mind.
Anyways, let us
proceed with our
first conics -
CIRCLES.

9. Circles
5
8
2
6
1
9
3
4
7

10. A circle is the locus of all points in
the plane having the same fixed
positive distance, called the radius,
from a fixed point called center. We
are going to discover how the circle’s
standard form was derived but
before that let us take a short detour
on distance between two points.
Circles
Distance Between Two Points
To get the distance between two
points and remember this:
𝑑=√( 𝑥2 − 𝑥1 )
2
+( 𝑦2 − 𝑦1)
2

11. Circles In the image, a circle with center
(h,k) which means the center NOT
on the origin and the radius r is the
segment from the center to a point
on the circle p. As we all know the
segment
|𝑃𝐶|=𝑟
Remember that the distance d
between two points is denoted by
𝑑=√( 𝑥2 − 𝑥1 )
2
+( 𝑦2 − 𝑦1)
2

12. Circles
This time, our points are C(h,k)
and P(x,y) so interchanging (h,k)
to and (x,y) to
From
|𝑃𝐶|=𝑟
√(𝑥 −h)2
+(𝑦 −𝑘)2
=𝑟
to
To remove the root sign (radical)
square both sides.
(𝑥 − h)2
+( 𝑦 − 𝑘)2
=𝑟2

13. Standard Equation of Circle
Center at (h,k)
Center at Origin (0,0)
(𝑥 − h)2
+( 𝑦 − 𝑘)2
=𝑟2
𝑥2
+ 𝑦2
=𝑟2

14. Example 1: Give the standard equation
of circle with the following given:
Center at Origin, radius 5.
Ans. 𝒙𝟐
+ 𝒚𝟐
=𝟐𝟓

15. Center (-2,6), radius
Example 2: Give the standard equation
of circle with the following given:
Ans.

16. Example 3: Give the standard equation
of circle with the following given:
Center (-4,3) tangent to y-axis.
Ans.

17. Example 4: Give the standard equation
of circle with the following given:
Center (-4,3) tangent to x-axis.
Ans.

18. General Equation of Circle:Determining
the center and radius of circle
Say we have a circle with an equation of , expanding this will give
us
Combining the like terms and equating this equation will give us
this is the general equation of circle
𝑥2
+ 𝑦2
+𝐶𝑥+ 𝐷𝑦+ 𝐹 =0
h
𝑤 𝑒𝑟𝑒𝐶∧𝐷≠0

19. Example 5:Determine the center and radius of the
following Circles through the given equation below.
Solution:
Regroup the terms
Completing the square (By completing the square, remember and since our
b=-5

20. Factoring our x in form
Therefore, our Center is and radius is

21. Example 6:Determine the center and radius of the
following Circles through the given equation below.
Solution:
Regroup the terms
Completing the square
(
Factoring the terms and simplifying the right hand side (it refers to the terms
on the right side of the equality sign)
So, our center is (1,2)and radius is 3