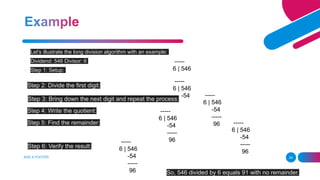
Computer arithmetic involves methods and techniques for performing arithmetic operations like addition, subtraction, multiplication, and division, primarily using binary representations. Efficient algorithms are crucial for optimizing performance, resource usage, and accuracy in various applications, including scientific computing and real-time systems. Techniques such as carry lookahead addition, two's complement subtraction, and the Karatsuba algorithm enhance speed, reduce complexity, and support large-scale computations in digital systems.