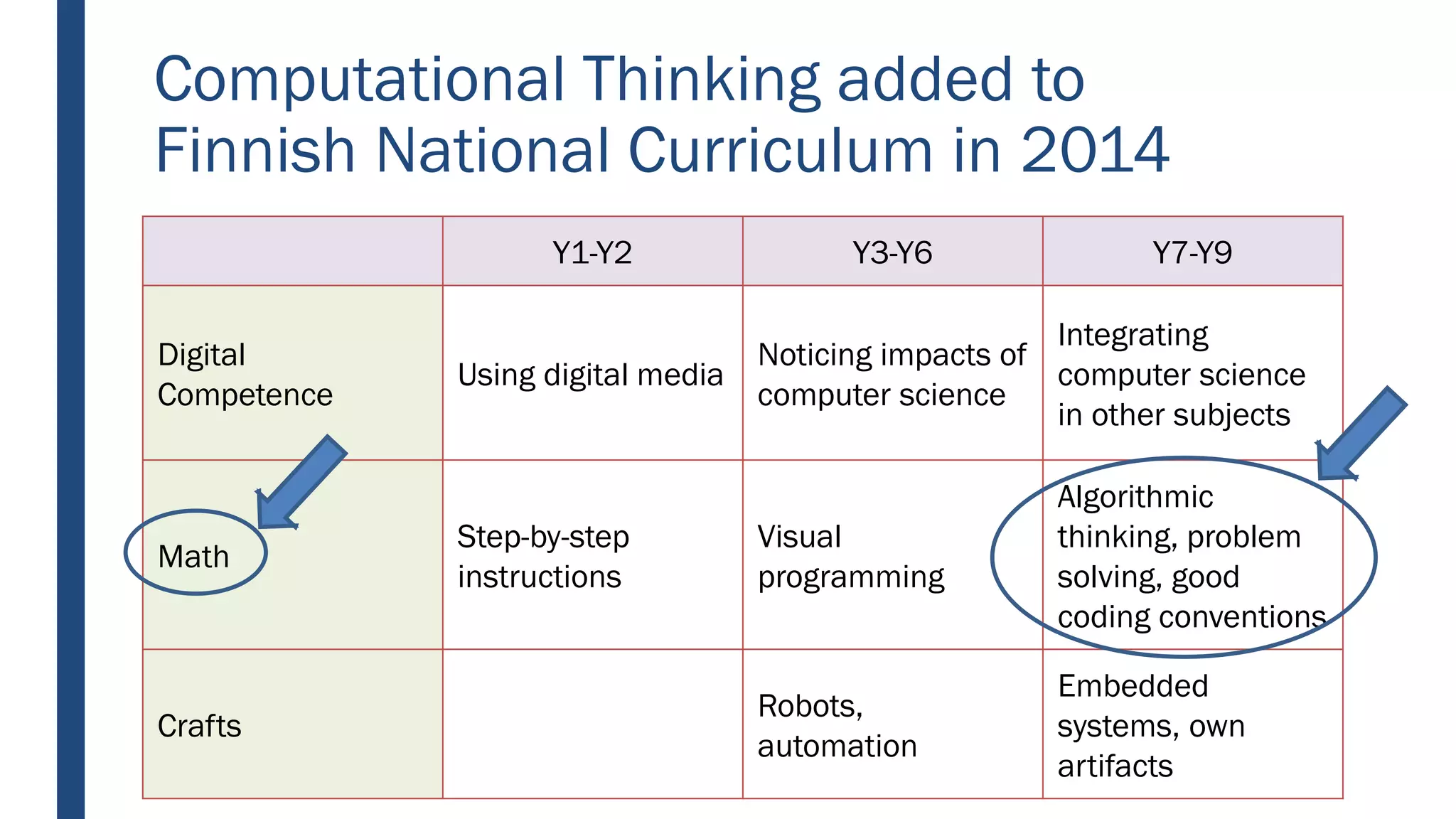
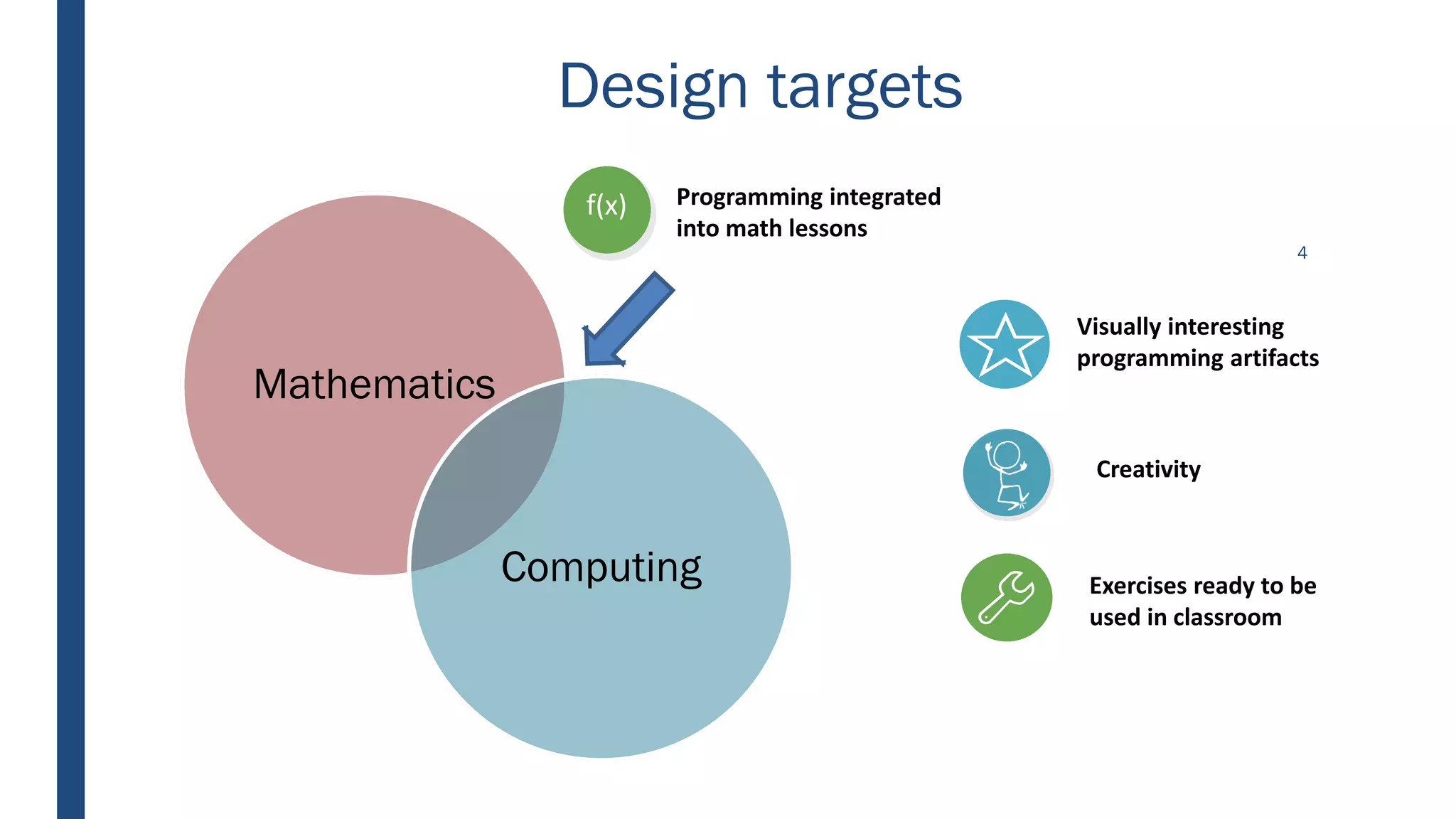
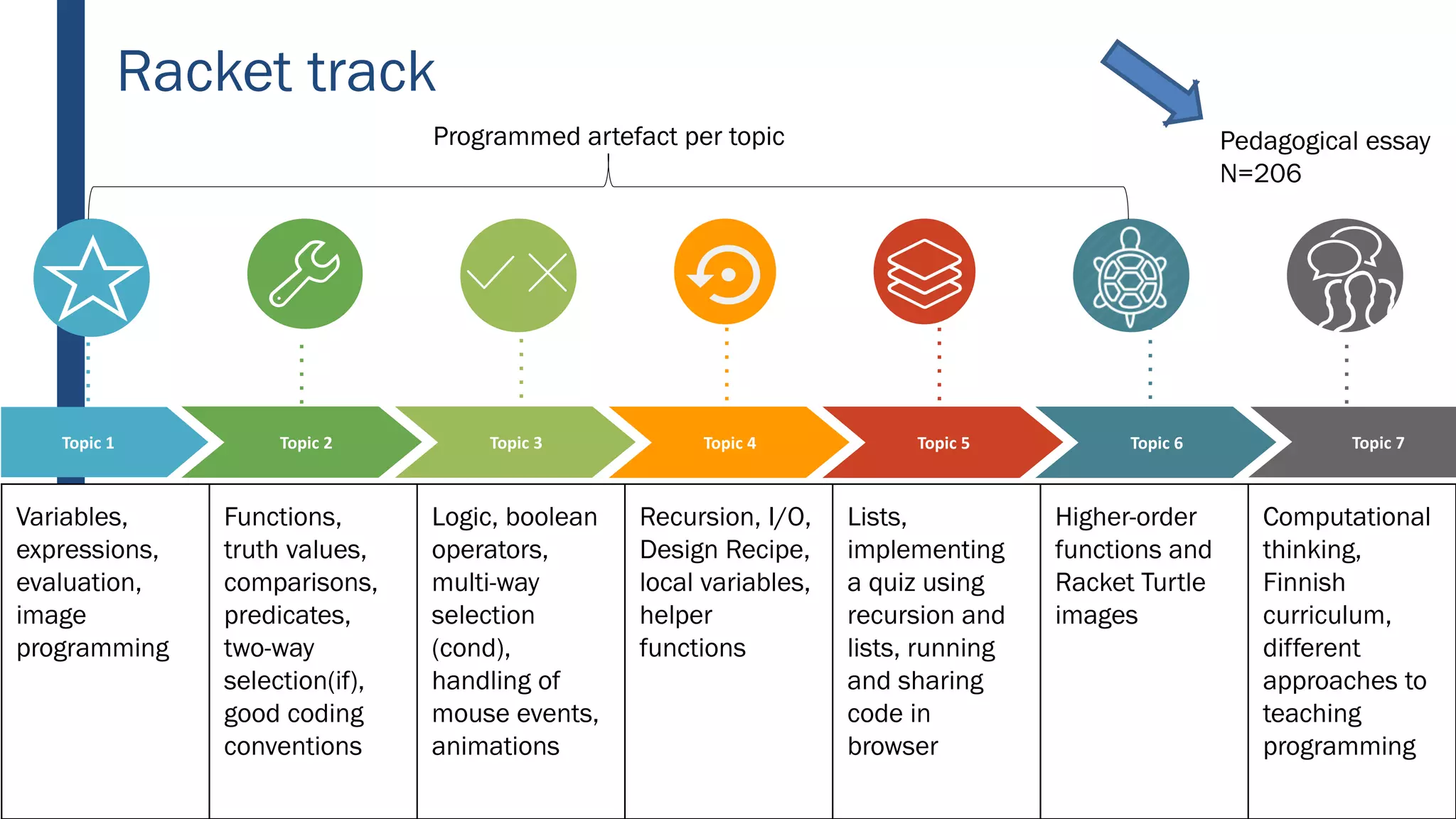
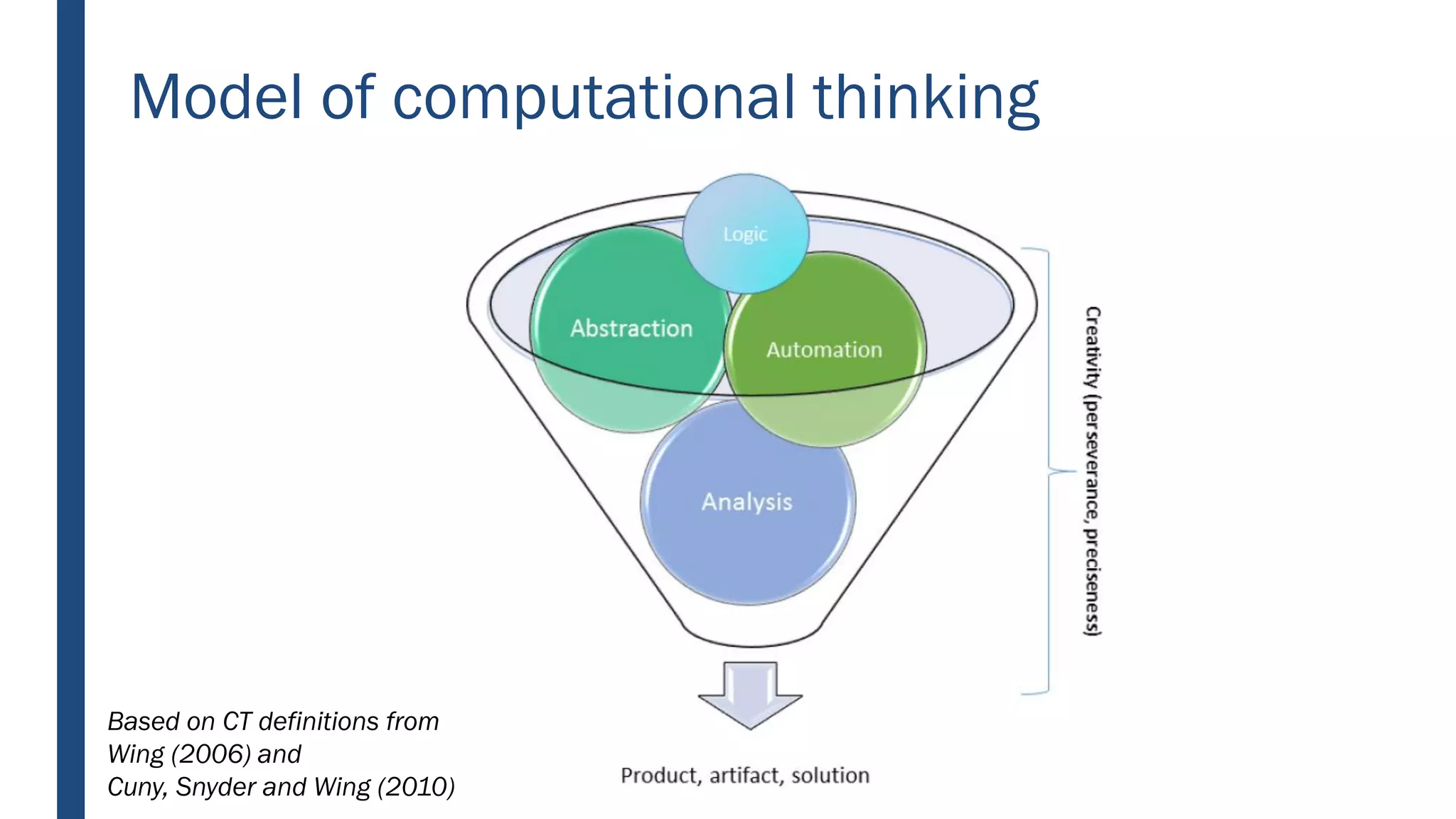
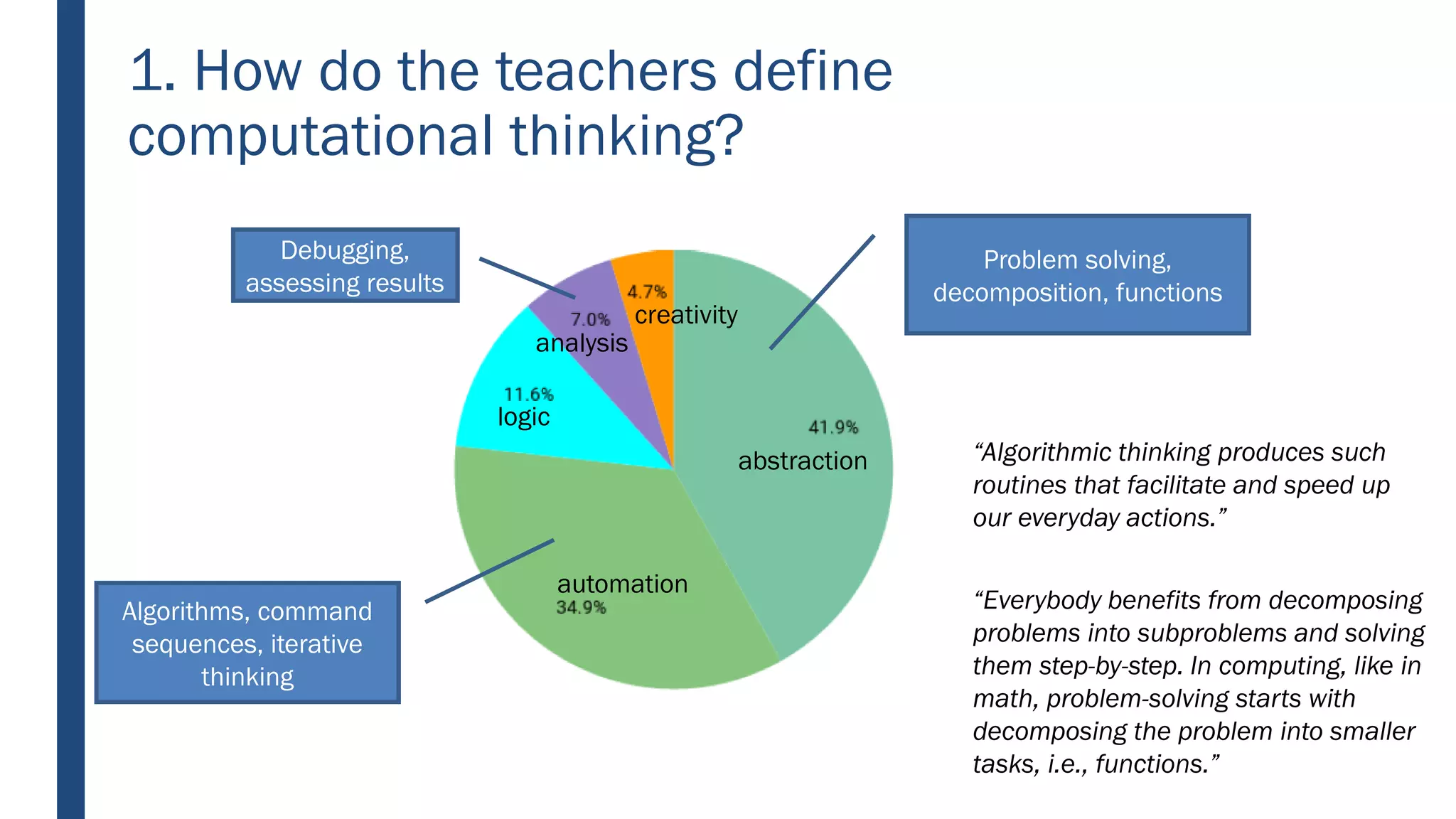
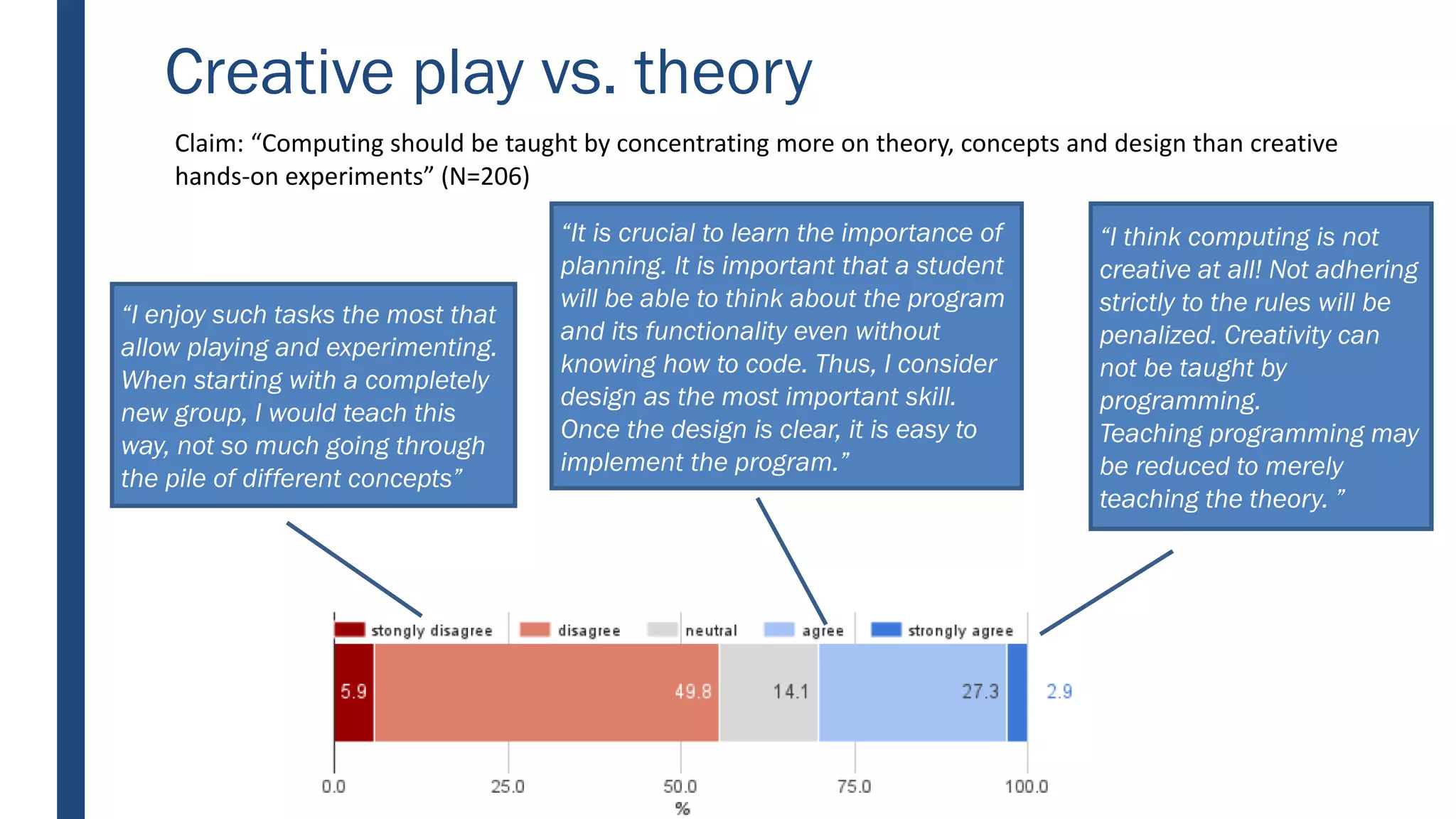
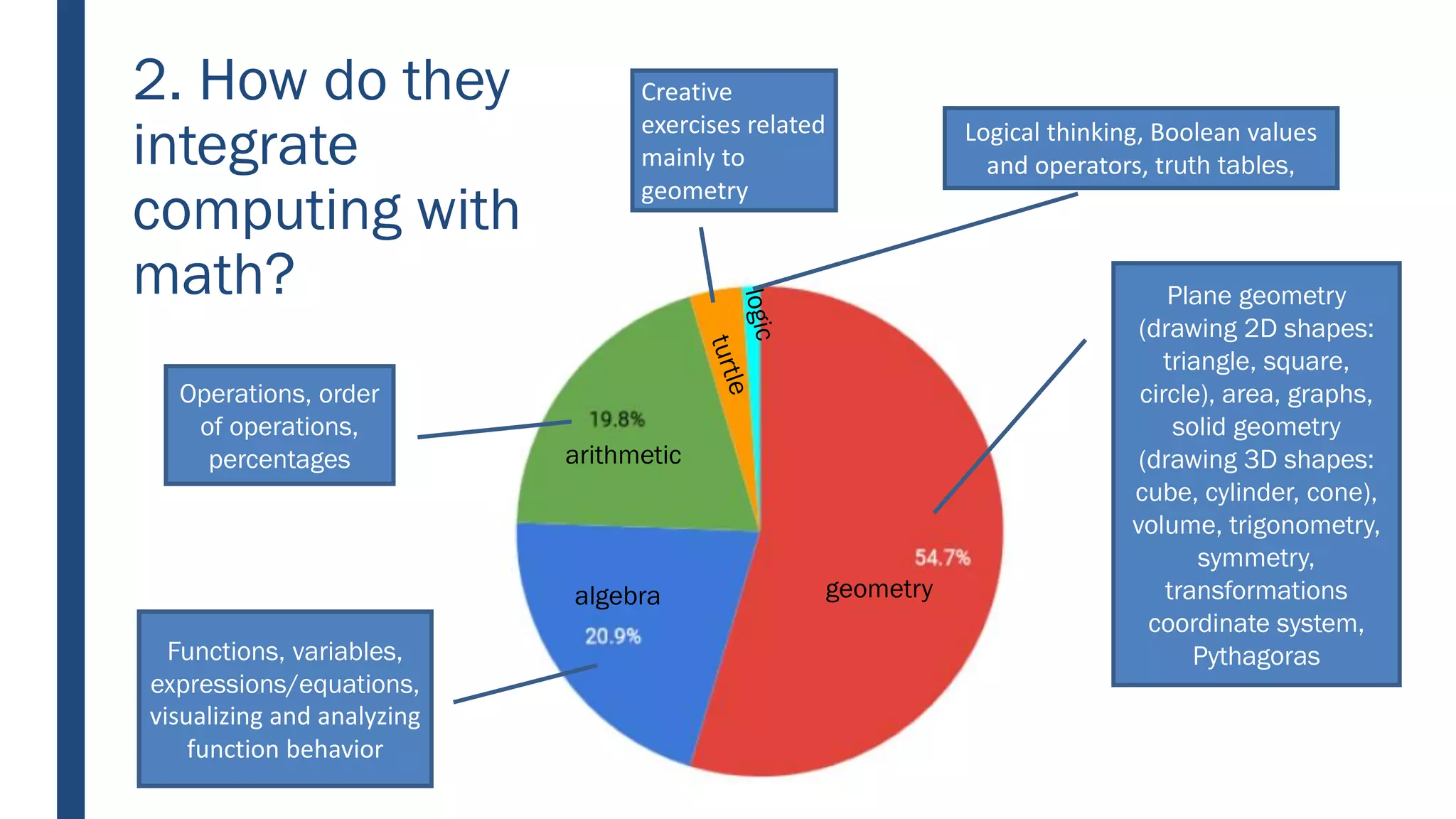
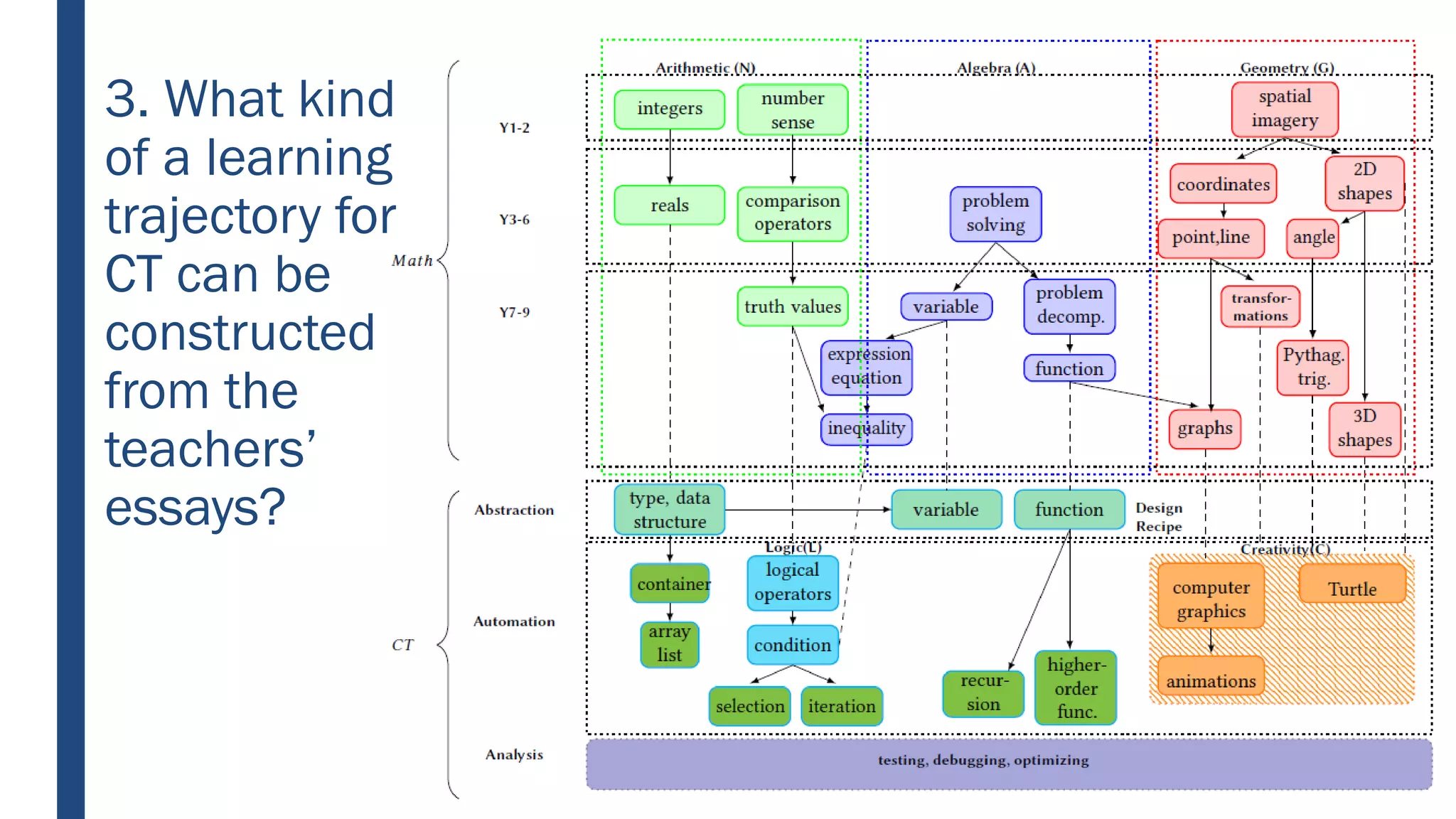
This document discusses integrating computational thinking into the Finnish national curriculum. It summarizes a MOOC course for teachers to learn computational thinking and programming using ScratchJr, Scratch, Racket, and Python. The document analyzes teacher essays on how they define and teach computational thinking, how they integrate it with math, and constructs a learning trajectory for computational thinking based on the essays. Key aspects of computational thinking discussed are abstraction, automation, logic, analysis, creativity, and problem solving.

1. Computational Thinking as an
Emergent Learning Trajectory of
Mathematics
Pia Niemelä, Tiina Partanen, Maarit Harsu,
Leo Leppänen, Petri Ihantola

2. Computational Thinking added to
Finnish National Curriculum in 2014
Y1-Y2 Y3-Y6 Y7-Y9
Digital
Competence
Using digital media
Noticing impacts of
computer science
Integrating
computer science
in other subjects
Math
Step-by-step
instructions
Visual
programming
Algorithmic
thinking, problem
solving, good
coding conventions
Crafts
Robots,
automation
Embedded
systems, own
artifacts

3. Code ABC MOOC
■ On-line course for in-service elementary school
teachers to learn computational thinking and
programming
■ Organized twice-a-year (2015-17)
■ Started/completed: 3649/1299
■ 2-3 credit points from Open University, University of
Helsinki
ScratchJr (Y1-2) Scratch (Y3-6)
Racket (Y7-9) Python (Y7-9)
Four tracks

4. Design targets
4
Visually interesting
programming artifacts
Creativity
Programming integrated
into math lessons
f(x)
Mathematics
Computing Exercises ready to be
used in classroom

5. Racket track
Topic 1 Topic 2 Topic 3 Topic 7Topic 4 Topic 5 Topic 6
Variables,
expressions,
evaluation,
image
programming
Functions,
truth values,
comparisons,
predicates,
two-way
selection(if),
good coding
conventions
Logic, boolean
operators,
multi-way
selection
(cond),
handling of
mouse events,
animations
Recursion, I/O,
Design Recipe,
local variables,
helper
functions
Lists,
implementing
a quiz using
recursion and
lists, running
and sharing
code in
browser
Higher-order
functions and
Racket Turtle
images
Computational
thinking,
Finnish
curriculum,
different
approaches to
teaching
programming
Programmed artefact per topic Pedagogical essay
N=206

6. Model of computational thinking
Based on CT definitions from
Wing (2006) and
Cuny, Snyder and Wing (2010)

7. 1. How do the teachers define
computational thinking?
abstraction
automation
logic
analysis
creativity
Problem solving,
decomposition, functions
Algorithms, command
sequences, iterative
thinking
Debugging,
assessing results
“Algorithmic thinking produces such
routines that facilitate and speed up
our everyday actions.”
“Everybody benefits from decomposing
problems into subproblems and solving
them step-by-step. In computing, like in
math, problem-solving starts with
decomposing the problem into smaller
tasks, i.e., functions.”

8. Creative play vs. theory
Claim: “Computing should be taught by concentrating more on theory, concepts and design than creative
hands-on experiments” (N=206)
“I think computing is not
creative at all! Not adhering
strictly to the rules will be
penalized. Creativity can
not be taught by
programming.
Teaching programming may
be reduced to merely
teaching the theory. ”
“It is crucial to learn the importance of
planning. It is important that a student
will be able to think about the program
and its functionality even without
knowing how to code. Thus, I consider
design as the most important skill.
Once the design is clear, it is easy to
implement the program.”
“I enjoy such tasks the most that
allow playing and experimenting.
When starting with a completely
new group, I would teach this
way, not so much going through
the pile of different concepts”

9. Inspired by creativity
Programming artifacts from topic 1
“Here is my owl. I wanted to include it
here, because while doing it I was
inspired like a child. The whole world
of coding, its opportunities and
creativity opened to me. I was capable
of doing this and the result was
unique!”

10. geometryalgebra
arithmetic
2. How do they
integrate
computing with
math? Plane geometry
(drawing 2D shapes:
triangle, square,
circle), area, graphs,
solid geometry
(drawing 3D shapes:
cube, cylinder, cone),
volume, trigonometry,
symmetry,
transformations
coordinate system,
Pythagoras
Operations, order
of operations,
percentages
Functions, variables,
expressions/equations,
visualizing and analyzing
function behavior
Logical thinking, Boolean values
and operators, truth tables,
Creative
exercises related
mainly to
geometry

11. 3. What kind
of a learning
trajectory for
CT can be
constructed
from the
teachers’
essays?

12. Thank you!
AnalysisAbstraction
Automation Logic
Creativity
For more information: Computational Thinking as an Emergent Learning
Trajectory of Mathematics in Proceedings of the 17th Koli Calling
International Conference on Computing Education Research