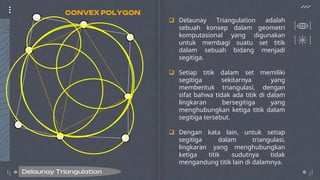
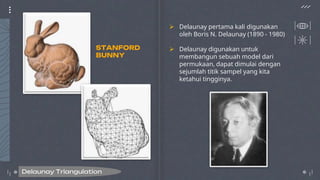
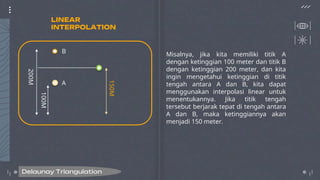
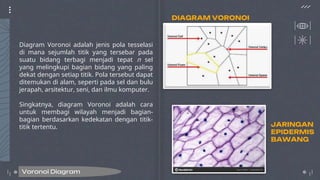
Dokumen ini membahas tentang computational geometry, khususnya Delaunay triangulation dan Voronoi diagrams, yang merupakan teknik dalam analisis dan pemodelan objek geometris. Delaunay triangulation digunakan untuk membangun model permukaan dengan titik sampel, sedangkan Voronoi diagram membagi area berdasarkan kedekatan ke titik-titik tertentu. Algoritma seperti Lloyd's digunakan untuk meningkatkan homogenitas sel dalam diagram Voronoi.