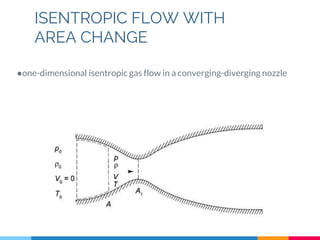
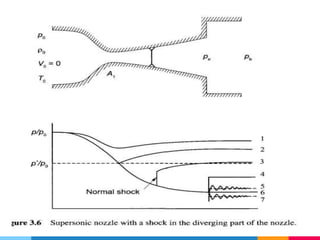
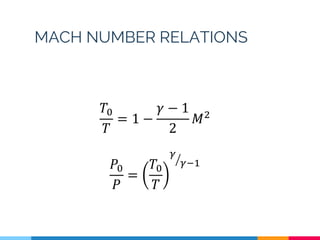This lecture covers compressible fluid flow through nozzles. It defines key concepts like Mach number and how it relates to the speed of sound. It describes isentropic flow through converging-diverging nozzles and how properties vary with Mach number. It also discusses diffusers, De Laval nozzles, and how choking occurs when flow reaches Mach 1 at the throat. The lecture concludes with a brief discussion of supersaturation in nozzle flows.

1. Course Title : Turbine Technology
Lecture 4:Compressible Flow

2. LAYOUT
🔌Learning Objectives
🔌Mach Number
🔌Mach Number Relations
🔌Isentropic Flow through nozzles
🔌Diffuser
🔌De Laval Nozzle
🔌Student Activity

3. LEARNING OBJECTIVES___
👉By the end of this lecture the student
should be able to understand:
○Compressible Fluid Flow Through Nozzles

4. MACH NUMBER AND THE
SPEED OF SOUND
●Sound waves are weak pressure waves,
𝑐 = 𝛾𝑟𝑇
●For air r = R/Mr = 8314/28.97 = 287J/(kg .K)
●γ = 1.4 the speed of sound
●eg. at T = 300 K is c = 347 m/s.
●For combustion gases properties are
assumed similar to air unless stated
otherwise
●E.g. at T = 1200 K it is c = 677.6 m/s.

5. MACH NUMBER AND THE
SPEED OF SOUND
●Mach number is the ratio of the local fluid
velocity v to the local sound speed c
𝑀 =
𝑉
𝑐
●Sonic M=1
●Subsonic M < 1
●supersonic M > 1
●hypersonic flows M » 1
●Transonic M ~ 1

6. MACH NUMBER RELATIONS
𝑇0
𝑇
= 1 −
𝛾 − 1
2
𝑀2
𝑃0
𝑃
=
𝑇0
𝑇
𝛾
𝛾−1

7. ISENTROPIC FLOW WITH
AREA CHANGE
●one-dimensional isentropic gas flow in a converging-diverging nozzle

8. ISENTROPIC FLOW WITH
AREA CHANGE
𝑚 = 𝜌𝐴𝑐 = 𝑐𝑡𝑒
ℎ 𝑜 = 𝑐𝑡𝑒
●in adiabatic flow ho is constant

9. Diffuser
●The static pressure decreases in the
downstream direction
●In subsonic flow(M<1) : increase in
area leads to decrease in velocity
●Thus a diffuser diverges in
downstream direction
●In supersonic flow(M<1) : increase in
area leads to increase in velocity
●Thus a diffuser converges in
downstream direction

10. de Laval nozzle
●In a continuously accelerating flow dV
> 0 at the throat where dA = 0 the flow
is sonic with M = 1.
●If the flow continues its acceleration
to a supersonic speed, the area must
diverge after the throat.
●The assumptions made in arriving at
these results are that the flow is steady
and one-dimensional and that it is
reversible and adiabatic

11. de Laval nozzle
●At sonic condition, denoted by the symbol (*), M = 1
●For γ=1
𝑇∗
𝑇0
=
2
𝛾 + 1
= 0,8333
𝑝∗
𝑝0
=
2
𝛾 + 1
𝛾
𝛾−1
= 0,5283
𝜌∗
𝜌0
=
2
𝛾 + 1
1
𝛾−1
= 0,6339
𝐴
𝐴∗
=
1
𝑀
2
𝛾 + 1
+
𝛾 − 1
𝛾 + 1
𝑀2
𝛾+1
2 𝛾−1

12. de Laval nozzle
●The flowrate is adjusted by a regulating valve
downstream of the nozzle.
●With the valve closed there is no flow and the
pressure throughout equals the stagnation
pressure.
●As the valve is opened slightly, flow is accelerated
in the converging part of the nozzle and its pressure
drops.
●It is then decelerated after the throat with rising
pressure such that the exit plane pressure pexit
reaches the backpressure pback

13. de Laval nozzle

14. de Laval nozzle
●Further opening of the valve drops the
backpressure and the flow rate increases until
the valve is so far open that the Mach number has
the value one at the throat and the pressure at
the throat is equal to the critical pressure p*.
●After the throat the flow diffuses and pressure
rises until the exit plane is reached.
●The pressure variation is shown as condition 2
in the figure.
●If the valve is opened further, acoustic waves to
signal what has happened downstream cannot
propagate past the throat once the flow speed
there is equal to the sound speed.
●The flow is now choked and no further
adjustment in the mass flow rate is possible.

15. de Laval nozzle
●The adjustment to the backpressure is now achieved
through a normal shock and diffusion in the diverging
part of the nozzle.
●This situation is shown as condition 3
●A weak normal shock appears just downstream of
the throat for backpressures slightly lower than that
at which the flow becomes choked, and as the
backpressure is further reduced, the position of the
shock moves further downstream until it reaches the
exit plane, which is shown as condition 4
●After this any decrease in the backpressure cannot
cause any change in the exit plane pressure.
●Condition 5 corresponds to an over-expanded flow,
since the exit pressure has dropped below the
backpressure and the adjustment to the backpressure
takes place after the nozzle through a series of oblique
shock waves and expansion fans.

16. SUPERSATURATION
●Consider a steam flow through a nozzle, with steam dry and
saturated at the inlet.
●As the steam accelerates through the nozzle, its pressure
drops, and, if the process were to follow a path of
thermodynamic equilibrium states, some of the steam would
condense into water droplets.
●As a consequence, the smaller the liquid droplet, the weaker is
the binding of the surface molecules.
●Hence liquid in small droplets is more volatile, and its
vaporization takes place at lower temperature than it would if
the phase boundaries were flat.
●In other words, at any given temperature vapor is formed
more readily from smaller droplets than from large ones, and
they can evaporate into a saturated vapor.
●This leads to supersaturation.

17. Any questions?

18. Next Lecture….
 Inserting boundary conditions in
Ansys
 Axial Turbines
 Turbine Stage
 Radial Turbines