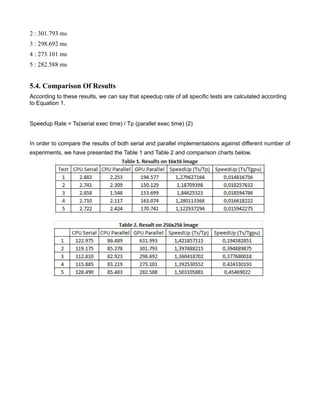
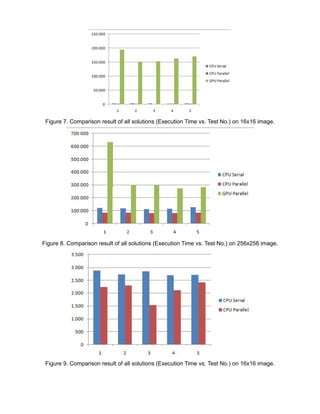
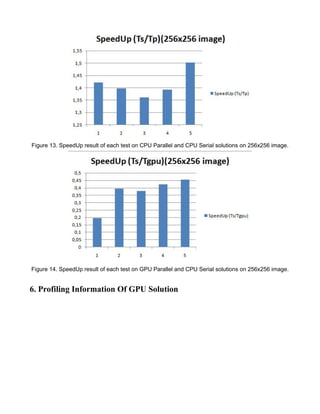
The document reports on a term project to design and implement serial and parallel solutions for an image processing algorithm. Experiments were conducted on 16x16 and 256x256 pixel images using C++ and CUDA. The CPU parallel solution was nearly 3 times faster than the GPU solution due to significant data transfer times between the CPU and GPU. While GPUs can provide massive parallelism, data transfers negated performance gains for this algorithm.

1. TERM PROJECT REPORT
OF
CMP641 SOFTWARE DEVELOPMENT FOR PARALLEL
COMPUTERS
Seval Çapraz
Graduate School of Science and Engineering, Hacettepe University
St. Number: N16146689
02.02.2019

2. 1. The Problem And Proposed Solution
In this document the design and implement of serial and parallel solutions are given for a image
processing problem. The algorithm is implemented using C++ and CUDA technologies. The algorithm
uses an image file with a 16-bit grayscale value. The experiments are done on 16x16 and 256x256 px
width and height version of Lena image which is given in Figure 1.
Figure 1. 256x256 16-bit grayscale image which is used in experiments
The intensity values are taken by using Matlab with imread() function. Then the intensity values
are saved in a comma separated file. This file is read by C++ and CUDA applications. To understand
the algorithm, 16x16 px image is used. The intensity values are given in Figure 2.
Figure 2. Intensity values of 16x16 px 16-bit grayscale image.
In the first step, a gradient value is calculated for each pixel. According to this calculation, if the
intensity of a pixel is lighter than all of its neighbors, it is labeled with a value of 0. If there are lighter
intensities in the neighborhood, the pixel is labeled to point the lightest. The label values are 1: N, 2:
NE, 3: E, 4: SE, 5: S, 6: SW, 7: W and 8: NW. The result of first step is given for 16x16 px image in the
Figure 3.

3. Figure 3. Result of first step for 16x16 px image.
In the second step, to determine the new label of the center pixel in the neighborhood of 7x7
pixels; The label value with the maximum count within the Manhattan distance of 4 is selected as the
label of the center pixel. There are 37 pixes in this Manhattan distance if the pixel is at the middle of
image. If the maximum count value is less than 9 (~25% of 37), the label of the center pixel will be
labeled with 0. By using the 16x16 image experiment, for example, lets calculate the the labels of
[3,3]:
0 0 0 0 0 -> 5 pieces
1 -> 1 pieces
2 2 2 2 2 -> 5 pieces
3 3 3 3 3 3 3 -> 7 pieces
4 4 4 4 4 4 4 4 -> 8 pieces
5 5 5 5 5 5 -> 6 pieces
6 6 6 -> 3 pieces
7 -> 1 pieces
8 -> 1 pieces
At most, there are label 4 among 37 pixels. However [3,3] = 0 beause total count of label 4 is less than
25%.
The first and second steps are done using different matrixes for results. Because it is run on
parallel approach therefore we can not wait for convolution of pixels. We used initial matrix to
calculate the neighborhood and save the result into another matrix. We used 1-D (1 dimensional)
approach to hold the matrixes in array structes. In this structure, we can hold whole rows and cols in
only 1 dimension. This made the solution available for GPU, therefore we can not copy 2-D arrays
from host to device in CUDA. We copied 1-D arrays easily. The first step can be run on parallel.The
second step can be run on parallel too. However second step must wait until the first step is finished.
The result of second step is given in Figure 4.

4. Figure 4. Result of second step for 16x16 px image.
In the third step, all gradient paths are identified in recursive function. The output is saved as a
vector in a data structure with has x1, y1, x2 and y2 for coordinates. The recurvice function is not
suitable for parallellism, therefore it run on only CPU. The result of third step is given in Figure 5 for
16x16 px image. The algorithm found 35 gradient paths and lists the result on console.
Figure 5. Result of third step of 16x16 px image.
For CPU parallel solution, 6 thread are used since there are 6 cores at the computer. For GPU
parallel solutions, the configuration is used as follows to create perfect fit for the images:
For 16x16 image:
dim3 block(1,1);
dim3 gridDim(16,16);

5. For 256x256 imge (because 8x32=256 is perfect fit):
dim3 block(32,32);
dim3 gridDim(8,8);
2. Hardware and Software Specifications
The algorithm found 35 gradient paths for 16x16 image, 7799 paths for 256x256 image. The
experiments are done 5 times for CPU Serial, CPU Parallel, GPU Parallel. CPU solutions are run with
C++ programming language with Ubuntu environment. The GPU solution is done on CUDA platform
in Ubuntu. The software information is given in below:
Operating System : Ubuntu 16.04 LTS x86_64 GNU/Linux
Processor : AMD Phenom(tm) II X6 1090T Processor × 6
Cores : 6
RAM : 16GB DDR3 1333 MHz
Compiler : NVCC (Nvidia Cuda Compiler CUDA Version 8.0.61) and g++ 5.4.0
NVIDIA Graphics Card : GeForce GTX 750 Ti
NVIDIA Driver Version : 375.26
CUDA Runtime version : 8.0.61
CUDA Capability Major/Minor version number: 5.0
Cuda device information can be seen at Figure 6.
Figure 6. Cuda Device Information
3. Required Libraries & Datasets
Source code for CUDA/GPU implementation can be found in the kernelgpu.cu file. This file includes

6. the libraries below:
#include "cuda_runtime.h"
#include <fstream>
#include <cstdlib>
#include <stdio.h>
#include <sys/time.h>
#include <iostream>
#include <sstream>
#include <vector>
#include <thread>
All the libraries common and comes with CUDA installation. The dataset is not used in project, only
lena_16g_lin.png image is used as a test image.
4. How To Run The Program
To comple cpp file of serial solution, run on terminale:
g++ -o kernelserial kernelserial.cpp
To run the program, run on terminale:
./kernelserial
To compile cpp file of parallel solution, run on terminale:
g++ -pthread -o kernelparallel kernelparallel.cpp -std=c++11
To run the program, run on terminale:
./kernelparallel
To compile CUDA file of GPU solution, run on terminale:
nvcc kernelgpu.cu -o kernelgpu
To run the program, run on terminale:
./kernelgpu
5. Results
5.1. Result of Serial Run
Execution time of 5 experiments on 16x16 px 16-bit grayscale image:
1 : 2.883 ms
2 : 2.741 ms

7. 3 : 2.858 ms
4 : 2.710 ms
5 : 2.722 ms
Execution time of 5 experiments on 256x256 px 16-bit grayscale image:
1 : 122.975 ms
2 : 119.175 ms
3 : 112.810 ms
4 : 115.885 ms
5 : 128.490 ms
5.2. Result of CPU-Parallel Run
Execution time of 5 experiments on 16x16 px 16-bit grayscale image:
1 : 2.253 ms
2 : 2.309 ms
3 : 1.548 ms
4 : 2.117 ms
5 : 2.424 ms
Execution time of 5 experiments on 256x256 px 16-bit grayscale image:
1 : 86.489 ms
2 : 85.278 ms
3 : 82.923 ms
4 : 83.219 ms
5 : 85.483 ms
5.3. Result of GPU-Parallel Run
Execution time of 5 experiments on 16x16 px 16-bit grayscale image:
1 : 194.577 ms
2 : 150.129 ms
3 : 153.699 ms
4 : 163.074 ms
5 : 170.741 ms
Execution time of 5 experiments on 256x256 px 16-bit grayscale image:
1 : 631.993 ms

8. 2 : 301.793 ms
3 : 298.692 ms
4 : 273.101 ms
5 : 282.588 ms
5.4. Comparison Of Results
According to these results, we can say that speedup rate of all specific tests are calculated according
to Equation 1.
Speedup Rate = Ts(serial exec time) / Tp (parallel exec time) (2)
In order to compare the results of both serial and parallel implementations against different number of
experiments, we have presented the Table 1 and Table 2 and comparison charts below.

9. Figure 7. Comparison result of all solutions (Execution Time vs. Test No.) on 16x16 image.
Figure 8. Comparison result of all solutions (Execution Time vs. Test No.) on 256x256 image.
Figure 9. Comparison result of all solutions (Execution Time vs. Test No.) on 16x16 image.

10. Figure 10. Comparison result of all solutions (Execution Time vs. Test No.) on 256x266 image.
Figure 11. SpeedUp result of each test on CPU Parallel and CPU Serial solutions on 16x16 image.
Figure 12. SpeedUp result of each test on GPU Parallel and CPU Serial solutions on 16x16 image.

11. Figure 13. SpeedUp result of each test on CPU Parallel and CPU Serial solutions on 256x256 image.
Figure 14. SpeedUp result of each test on GPU Parallel and CPU Serial solutions on 256x256 image.
6. Profiling Information Of GPU Solution

12. Figure 7.
Figure 8.
Figure 9.
Figure 10.
7. Conclusion
In conclusion, this report mainly discusses how to solve an image processing problem in different
parallelism styles. We inspected results of parallelization on both CPU and GPU. Parallel
implementation of algorithm provides better solutions as compared to serial implementation. However,
GPU solution gives worse results than CPU based parallel solution. The main reason of it, the data

13. transfer of matrixes took a lot of execution time. The statistical results provide that CPU based
parallelized approach of this image processing problem is nearly 3 times faster than GPU solution
because we transfer 3 matrixes. The CPU paralle solution is 0.5 times faster than serial solution. We
assume GPU based parallel solution using NVIDIA CUDA platform might be the fastest solution so far
thanks to the massive parallelization capabilities of GPUs and optimization techniques on GPU
programming. GPU solution usually makes algorithm faster than both the recent serial and parallel
CPU-based ones. However this sometimes does not work because of huge amoung of data copy and
transfer jobs.
***