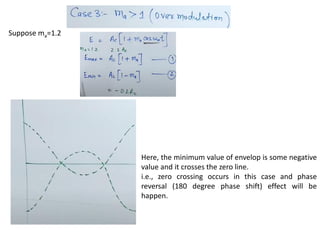
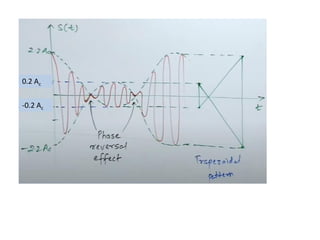
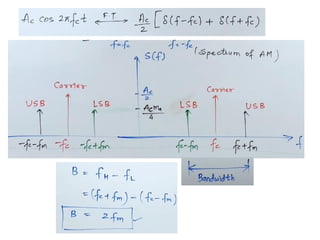
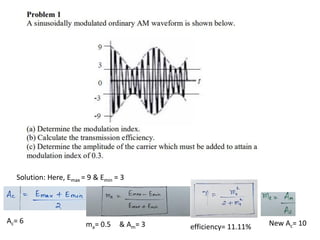
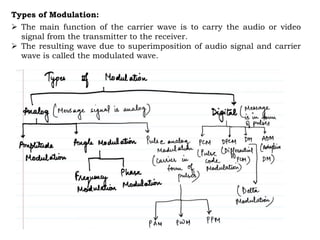
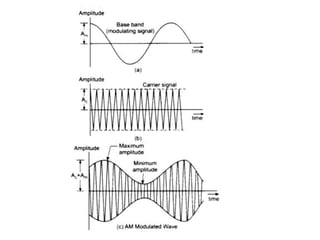
The document discusses amplitude modulation (AM), which is a process of superimposing a low frequency signal on a high frequency carrier signal. AM varies the amplitude of the carrier wave based on the instantaneous value of the modulating signal. This allows information to be transmitted over long distances using radio waves. Key points include: AM produces an output signal with sidebands having frequencies that are the sum and difference of the carrier and modulating signal frequencies. The bandwidth of an AM signal is twice the frequency of the modulating signal. Modulation index indicates how much the carrier is modulated and must be less than 1. Power transmission efficiency of AM is low. Examples demonstrate calculating modulation index, frequencies, and bandwidth from given AM signals.

1. Communication System
Module-2

2. Modulation
Introduction to Modulation:
 Modulation is the process of superimposing a low frequency signal on
a high frequency carrier signal. The transmitter modifies the message
signal into a suitable form for transmission over the channel.
 The process of modulation is defined as varying the RF carrier wave
in accordance with the information in a low frequency signal.
 Modulation is defined as the process by which some characteristics
such as amplitude, frequency and phase, of a carrier is varied in
accordance with instantaneous value of the modulating signal.

3. Need for Modulation:
The following are the factors which emphasize the need for
modulation:
 Antenna Height
 Narrow Banding
 Poor radiation and penetration
 Diffraction angle
 Multiplexing

4. Ex-1:
 If two musical programs were played at the same time within distance, it
would be difficult for anyone to listen to one source and not hear the
second source. Since all musical sounds have approximately the same
frequency range, from about 50 Hz to 10 KHz. If a desired program is
shifted up to a band of frequencies between 100 KHz and 110 KHz, and
the second program shifted up to the band between 120 KHz and 130
KHz, Then both programs gave still 10 KHz bandwidth and the listener
can (by band selection) retrieve the program of his own choice. The
receiver would down shift only the selected band of frequencies to a
suitable range of 50Hz to 10 KHz.
Ex-2:
 A second more technical reason to shift the message signal to a higher
frequency is related to antenna size. It is to be noted that the antenna
size is inversely proportional to the frequency being radiated. This is 75
meters at 1 MHz but at 15 KHz it has increased to 5000 meters a vertical
antenna of this size is impossible.

5. Types of Modulation:
 The main function of the carrier wave is to carry the audio or video
signal from the transmitter to the receiver.
 The resulting wave due to superimposition of audio signal and carrier
wave is called the modulated wave.

7. Amplitude Modulation (AM)
 Amplitude modulation is the process of changing the amplitude of high
frequency carrier signal according to the instantaneous value of the
modulating signal.
 i.e., in AM, the amplitude of the carrier wave is varied in accordance
with the modulating signal while the frequency of the carrier wave
remains constant.
 It is the oldest mode of modulation which is most widely used.
 Modulating signal contains information and is also known as message
signal or baseband signal.
 Any communication system involves carrier signal which is sinusoidal in
nature.
 AM is done by an electronic device called “modulator”.

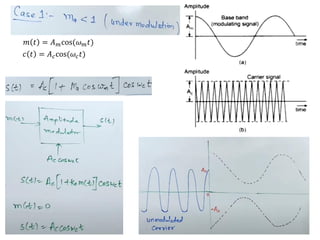
9.  Let the modulating signal is represented as:
 The fundamental carrier signal is represented as:
Frequency of modulating signal
Amplitude of modulating signal
Mathematical Expression of AM wave
 Carrier signal contains no information and has frequency
higher than that of modulating signal.
𝑚 𝑡 = 𝐴𝑚cos(2𝜋𝑓𝑚𝑡)
𝑚 𝑡 = 𝐴𝑚cos(𝜔𝑚𝑡) (1)
(2)
𝑐 𝑡 = 𝐴𝑐cos(𝜔𝑐𝑡)
𝑐 𝑡 = 𝐴𝑐cos(2𝜋𝑓𝑐𝑡)
Frequency of carrier signal
Amplitude of carrier signal
𝑖. 𝑒. , 𝑓𝑐 ≫ 𝑓𝑚 𝑜𝑟 𝜔𝑐 ≫ 𝜔𝑚 (3)
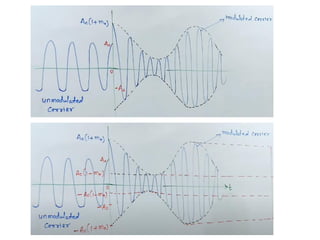
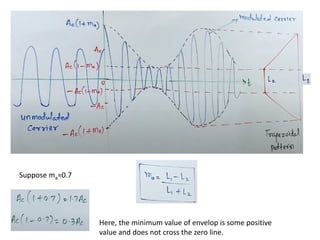
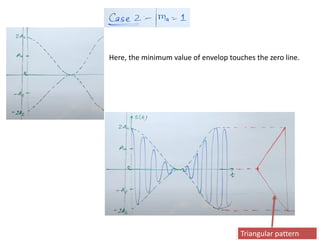
 The amplitude modulated signal can be represented as:
𝑐𝑚 𝑡 𝑜𝑟 𝑠(𝑡) = [𝐴𝑐+𝑚(t)] cos(2𝜋𝑓𝑐𝑡) (4)

10. 𝑐𝑚 𝑡 = 𝐴𝑐 1 +
1
𝐴𝑐
𝑚 t cos(2𝜋𝑓𝑐𝑡)
𝑐𝑚 𝑡 = 𝐴𝑐 1 + 𝐾𝑎𝑚 t cos(2𝜋𝑓𝑐𝑡)
 Where,
𝐾𝑎 =
1
𝐴𝑐
= 𝐶𝑜𝑛𝑠𝑡𝑎𝑛𝑡 𝑐𝑎𝑙𝑙𝑒𝑑 𝐴𝑚𝑝𝑙𝑖𝑡𝑢𝑑𝑒 𝑆𝑒𝑛𝑠𝑖𝑡𝑖𝑣𝑖𝑡𝑦 𝑜𝑓 𝑡ℎ𝑒 𝑚𝑜𝑑𝑢𝑙𝑎𝑡𝑜𝑟
 It is measured in 𝑉𝑜𝑙𝑡−1
 Using (1) & (4):
𝑐𝑚 𝑡 = [𝐴𝑐+𝐴𝑚 cos 2𝜋𝑓𝑚𝑡 cos(2𝜋𝑓𝑐𝑡)
𝑐𝑚 𝑡 = 𝐴𝑐[1 +
𝐴𝑚
𝐴𝑐
cos 2𝜋𝑓𝑚𝑡 cos(2𝜋𝑓𝑐𝑡)
𝑐𝑚 𝑡 = 𝐴𝑐[1 + 𝜇 cos 2𝜋𝑓𝑚𝑡 cos(2𝜋𝑓𝑐𝑡)
 Where, 𝜇 𝑜𝑟 𝑚𝑎 =
𝐴𝑚
𝐴𝑐
= 𝑖𝑠 𝑎 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛𝑙𝑒𝑠𝑠 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 &
𝑖𝑠 𝑘𝑛𝑜𝑤𝑛 𝑚𝑜𝑑𝑢𝑙𝑎𝑡𝑖𝑜𝑛 𝑖𝑛𝑑𝑒𝑥 𝑜𝑟 𝑚𝑜𝑑𝑢𝑙𝑎𝑡𝑖𝑜𝑛 𝑓𝑎𝑐𝑡𝑜𝑟 𝑜𝑟 𝑑𝑒𝑝𝑡ℎ 𝑜𝑓 𝑚𝑜𝑑𝑢𝑙𝑎𝑡𝑖𝑜𝑛
𝜇 𝑜𝑟 𝑚𝑎 ≪ 1
 Modulation index is the measure of how much a modulating signal
modulates the carrier signal.

12. 𝑁𝑜𝑤 𝑐𝑚 𝑡 = 𝐴𝑐 cos 𝜔𝑐𝑡 + 𝐴𝑐𝜇 cos 𝜔𝑐𝑡 cos(𝜔𝑚𝑡)
𝑐𝑚 𝑡 = 𝐴𝑐 cos 𝜔𝑐𝑡 +
𝐴𝑐𝜇
2
2 cos 𝜔𝑐𝑡 cos(𝜔𝑚𝑡)
𝑐𝑚 𝑡 = 𝐴𝑐 cos 𝜔𝑐𝑡 +
𝐴𝑐𝜇
2
[cos 𝜔𝑐 + 𝜔𝑚 𝑡 + cos 𝜔𝑐 − 𝜔𝑚 𝑡]
2 cos 𝐴 cos 𝐵 = cos 𝐴 + 𝐵 + cos(𝐴 − 𝐵)
𝑐𝑚 𝑡 = 𝐴𝑐 cos 𝜔𝑐𝑡 +
𝐴𝑐𝜇
2
cos 𝜔𝑐 + 𝜔𝑚 𝑡 +
𝐴𝑐𝜇
2
cos 𝜔𝑐 − 𝜔𝑚 𝑡
So, the expression of amplitude modulated wave is:
Carrier
Sideband
Upper Sideband
(USB)
Lower Sideband
(LSB)

13. Important points:
 Amplitude of carrier is 𝐴𝑐 (Volts)
 Frequency of carrier is 𝑓𝑐=𝜔𝑐/2𝜋
 Amplitude of modulating or message signal is 𝐴𝑚 (Volts)
 Frequency of modulating or message signal is 𝑓𝑚=𝜔𝑚/2𝜋
 Amplitude of USB =
𝐴𝑐𝜇
2
= Amplitude of LSB
 Frequency of USB 𝑓𝑈𝑆𝐵 = 𝑓𝑐 + 𝑓𝑚
 Frequency of LSB 𝑓𝐿𝑆𝐵 = 𝑓𝑐−𝑓𝑚

14. Bandwidth of Amplitude modulated wave:
∆𝜔 = 𝑓𝑈𝑆𝐵 − 𝑓𝐿𝑆𝐵
∆𝜔 = 𝜔𝑐 + 𝜔𝑚 − (𝜔𝑐 − 𝜔𝑚)
∆𝜔 = 2𝜔𝑚
(i. e. , twice of frequency of modulating signal)
Spectrum of AM

16. Single Tone Amplitude Modulation
 If the modulating or baseband signal consists of only one (single)
frequency i.e., modulation is done by a single frequency or tone, then
this type of amplitude modulation is known as single tone amplitude
modulation.
 Expression of Single Tone AM signal is written as follows:

17. Time Domain Representation of Amplitude Modulation
 Expression of Single Tone AM signal is written as follows:
 Envelope of the above signal is:

19. 𝑚 𝑡 = 𝐴𝑚cos(𝜔𝑚𝑡)
𝑐 𝑡 = 𝐴𝑐cos(𝜔𝑐𝑡)

21. Suppose ma=0.7
Here, the minimum value of envelop is some positive
value and does not cross the zero line.

22. Triangular pattern
Here, the minimum value of envelop touches the zero line.

23. Suppose ma=1.2
Here, the minimum value of envelop is some negative
value and it crosses the zero line.
i.e., zero crossing occurs in this case and phase
reversal (180 degree phase shift) effect will be
happen.

24. -0.2 Ac
0.2 Ac

25. Frequency Domain Representation of Amplitude Modulation
 Expression of Single Tone AM signal is written as follows:

27. Power Calculation in Amplitude Modulation
Note: If resistance is not given then assume R = 1

29. Transmission Efficiency

31. Solution: Here, Emax = 9 & Emin = 3
Ac= 6 ma= 0.5 efficiency= 11.11% New Ac= 10
& Am= 3

32. Problem 2:
A carrier wave of frequency f = 1mHz with a pack voltage of 20V is used to modulate
a signal of frequency 1kHz with a pack voltage of 10v. Find out the following:
(i) Modulation index
(ii) Frequencies of the modulated wave
(iii) Bandwidth

33. Problem 3:
y = 10 cos (1800 πt) + 20 cos 2000 πt + 10 cos 2200 πt. Find the modulation index
(μ or ma) of the given wave.
Solution:
As we know, the expression for amplitude modulated wave is
s(t) = Ac (1+ μ cos ωmt) cos ωct
S(t) = (Ac + Am cos ωmt) cos ωct ……………… (1)

35. Problem 4:
Solution:
Ac= 20
& Am= 10
Pc= (Ac)^2/2