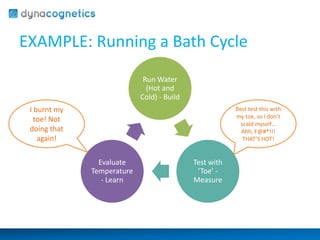
The document provides an introduction to A/B testing, emphasizing its importance in predicting outcomes in uncertain environments. It discusses how controlled experiments can help evaluate variables systematically and outlines the necessary principles for designing effective tests. Additionally, it highlights common tools and statistical concepts relevant to A/B testing, while cautioning against various statistical errors.

1. A/B-Testing: An Introduction
What is it? Why Use it?

2. Prediction in Predictable Environments
Predictable Models Excel in Deterministic
Environments
Statics & Dynamics Don’t Change
• ‘Fitness’ for purpose always
measured the same
• Frictionless Pendulum swing Very
Predictable
– Simple Harmonic Motion
• Control Systems
– e.g. Anti-lock Braking System
Sacrilege:
Learning is pointless (it’s all known), thus
Waterfall/Heavy Development Methods
Excel! :-O
Time Period give by

3. Uncertain/Unpredictable Contexts
• Human Interaction
Uncertain.
• Everyone is…
– Different
– [Relatively] fickle
– Growing Older
– Influenced By Other Stuff
– …
• Definition of fitness for
purposes changes
• In fact, Everything
Changes!

4. Story of the Foot
• Once upon a time there was a foot which Belonged to the
King of a Powerful Kingdom
• He Reigned Supreme because All Swords Had to be 7 ft
Long
• King dies naturally and a new King is Coronated
• But he has a Big Ego and Really Small Feet
– Half the length of Previous King
• He Ordains All Swords Now not Fit for Purpose
• So they’re Melted & Remade to 7 of his feet
• Along come Evil Army with swords now Twice as Long
• Nobody in the Kingdom Lived Happily Ever After! :-(

5. Q: HOW CAN WE EVER BE
PREDICTABLE?

6. Pick Your Tool: Certainty v Uncertainty
Predictable Environments
• Lots known up front
• ‘Variables/factors’ can all be identified…
• …So can predict with high certainty
where whole systems will be in t time-steps
– seconds, minutes, hours, days, weeks,
months, years…
• Little Need to Adapt
• Most appropriate for Standards Models
– SI Units
– HTTP/SMTP/POP3…
• ‘Dictate works’, not nice, but true
• e.g. ‘7ft’ Swords will have continued to
exist
– Even if the heads of the blacksmiths didn’t.
Uncertain Environments
• Very little known up front
• Variable levels of traffic,
experience etc.
• ‘Fitness function’ itself
changes
– e.g. King changes = Foot
changes
• Continual need to check the
fitness function…
– e.g. Customer reviews,
performance metrics
• Infers Continual Need to
Change/Improve Systems

7. EXAMPLE: Running a Bath (Uncertain)
Predictable Models
• Don’t know the water temperature
• Never done it before
1. Put hot tap on for 5 minutes
2. Cold Tap on for 2 minutes
3. Get in
Risks
Scolding your Jewels and More!
Uncertainty Models
• Don’t know the water temperature
• Never done it before
1. Put hot tap on for 5 seconds
2. Put cold tap on for 2 seconds
3. Dip toe in
4. If
• Too hot add cold water
• Too cold add hot water
• Else get in & relax
5. Go to 1 (Rinse, Repeat)
Risks
Slightly more time to get to ideal
temperature, but gets there with much less
risk of burning crucial elements and
potential less water waste.

8. EXAMPLE: Running a Bath Cycle
Run Water
(Hot and
Cold) - Build
Test with
‘Toe’ -
Measure
Evaluate
Temperature
- Learn
Best test this with
my toe, so I don’t
scald myself…
Ahh, F@#*!!!
THAT’S HOT!
I burnt my
toe! Not
doing that
again!

9. Dealing with Uncertainty
• More variables than equations to solve them…
• …Hence optimisation problem (no unique solution)
• Like it or not, iterative cycles work best
– Build-Measure-Learn; DMAIC
• Frequent Experiments & Actionable Change
• Control by Experimental Design Principles
– Test one change in isolation
– Compare against a control group/result
– Randomise Groupings
– Double Blind
• Plus, smaller tasks = smaller variance = greater certainty
Gold Standard: Randomised Double Blind Controlled Trial

10. Definition: Randomised
• Two groups
• Randomly Assign
Subjects to Each Group

11. Definition: Double Blind
Both Researcher & Subject
Don’t know which group
they are assigned to.
So researcher and subject
behave the same for A
and B tests.
TIP: Automated allocation
Image via ’John the Math Guy’

12. Definition: Controlled
Every potential factor is
fixed aside from the factor
under test.
Minimises ‘confounding
variables’
e.g. If someone goes outside and
gets wet, does it mean it’s raining?
Image via ‘Not the average’ blog

13. Designing Experiments
• Start with Hypothesis
– Include theory if analytical
• Experiment AGAINST a control group!
– Control Group = Baseline to compare against (B-test)
– Experimental Group is A-test
• Randomly Allocate Control & Experimental Group
– Ideally Researcher & Subject Can’t Know
• Analyse Results, Conclude AND Act!

14. Caution
• Change only one thing at once!
– Can do A/B/n tests, but have to be linearly independent variables
• statistically, not a certainty!
• Objective: Make sure results aren’t by chance (e.g. against placebo)!
• Analyse against ‘Null’ Hypothesis
– Opposite of what you are trying to prove
• Factor in type 1 & 2 statistical errors
– False positive and Negatives
• Your test is alternate hypothesis
• If Null hypothesis (Chance) is very very small, accept Alternate
hypothesis…
– ‘Small-p’ = probability null hypothesis is true
• …which you are trying to prove!
• Otherwise, no choice but to accept null hypothesis

15. Q: Where Can A/B-testing Be Used?
A: EVERYWHERE!

16. Where Can A/B-Tests Be Used?
• Guerrilla testing
• Lean-Startup A/B-Tests (tech, marketing etc.)
• Pilots
• Experiments
• Proof of Concepts
• Software Development Team Retrospectives
• Manufacturing Processes
• Change Programmes
• Departmental Effectiveness
• …

17. Q: What tools can we use?
A: STATISTICS

18. Toolbox: Normal Distribution
Data that is normally distributed
shown as a continuous line.
Fixed width histogram = Same
(right)
Pros:
1. Incredibly diverse
2. Tables/Excel Functions exist
Cons:
1. Needs many samples (25+)
– Errors significantly impact
result & need other ways (e.g.
t-test)
2. Can’t Always Force Normality
– But story point estimates can!
Source: Critical Numbers Group Sheffield University

19. Toolbox: Confidence Intervals
Indicates reliability of estimate, given
data = Likelihood that result falls
within values of x-standard
deviations of the mean.
Answers “How sure are you that this
result was expected?”
Pros:
1. Easy to do
2. Excel Functions/Libraries exist
Cons:
1. Same weakness as normal
distribution
2. Arbitrary confidence intervals
– Researcher chooses, but 95%
defacto standard (2 sigma)
Source: Moz.com

20. Toolbox: Correlation Matrix
Matrix of elements. Each is
correlation coefficient of data v data.
“How strongly does this relate to
that?”
High correlation -> dig deeper
Pros:
1. Excel Functions/Libraries exist
Cons:
1. Correlation isn’t Causation!
2. More of a ‘faff’ in Excel
– Prone to human error in analysis
Source: Genome biology

21. Toolbox: Factor Analysis
Using correlation matrix to identify
factors, determine independent
variables for dependent variables.
Pros:
1. Linear Algebra tools to help
2. Identifies combinations of
factors
Cons:
1. Excel doesn’t support it native
2. ‘Cancelling’ factors or
confounding factors problematic
3. Have to understand linear
algebra
4. Basically an approximation (so
what’s good enough?)
Source: Kovach Computing Services

22. Definitions
TERM DESCRIPTION
Dependent Variable A variable that depends on one or more other
variables (y = x + 2, y is dependent, x is independent)
Independent Variable A variable that does not depend on the value of any
other variable.
Confounding Variable A variable that could independently present the same
result as some other variable. This reduces the
credibility and certainty of a result (e.g. if I go outside
and I get wet, is it because it was raining?)
Distribution The ‘shape’ of the graph of a random variable
Type 1 Error (False
Positive)
Declaring a result as confirmed when it’s not, usually
through experimental error.
Type 2 Error (False
Negative)
Declaring a result as false when it’s true. Usually by
experimental or interpretive error..

23. Thanks for Viewing
Further Reading
Random Variables and Probability Distributions
https://www.khanacademy.org/math/probability/random-variables-topic/
random_variables_prob_dist/v/random-variables
Khan Academy
Confidence Intervals
http://en.wikipedia.org/wiki/Confidence_interval
Normal Distribution
http://en.wikipedia.org/wiki/Normal_distribution
“Correlation & Dependence” Wikipedia
http://en.wikipedia.org/wiki/Correlation_and_dependence
Factor Analysis
http://en.wikipedia.org/wiki/Factor_analysis
Genome Biology
http://genomebiology.com/
Publishes research, software and new methods
Ethar Alali @EtharUK @Dynacognetics
Managing Director & Chief Architect
Polymath-MathMo. Programming since 9 years old. TOGAF 9 Certified, change agent.
Blog: GoadingtheITGeek.blogspot.co.uk
About Us
Specialist ICT Strategists & Advisors.
Member of HiveMind Network for some of
the biggest household and corporate multi-nationals.
Accredited Growth Voucher Advisors
certified to deliver IT & Web Growth
Consultancy as part of the government’s
Growth Voucher Scheme.
Accreditations & Associations