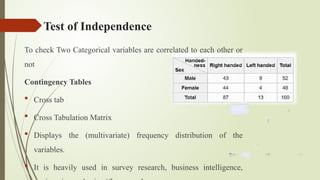
Chi-Square (χ²) Test — a fundamental statistical tool used to assess relationships between categorical variables. It covers the types of Chi-Square tests (Goodness of Fit and Test of Independence), assumptions, formula, step-by-step calculation, and interpretation of results. Examples and visual aids are included for better understanding. Ideal for students, researchers, and professionals in statistics, data science, social sciences, and biology.

1. Government College University Faisalabad
Chi-Square Test
Presented to :
Sir Irfan Ali Raza
Presented by :
Irum Arshad (247124)
Zunaira Hameed (247121)
Maria Batool (247122)
Musaab Sohail (247130)

2. Chi-Square Test (non parametric Test)
 A chi-square (x²) statistic is a test that measures how Expectations
compare to actual observed data.
 Data Collected (Observed) ← === → Data Predicted (Expected)
 Null Hypothesis Observed = Expected
 Alternate Hypothesis → Observed ≠ Expected

3. CHI Square performs Two types of Test
 Goodness of Fit Test
 (Single C Variable)
 The test of independence
 (Between Multiple C Variables)

4. Goodness of fit test
The goodness of fit test is a statistical hypothesis test to see how well sample
data fit a distribution from a population with a normal distribution. Fit Test
Defining a Null and Alternate Hypothesis
 Null Hypothesis: ratio of 50-50 exists in office
 Alternate Hypothesis in office: Raito of 50:50 is not there.
 Males employees < Female Employees
 Males employees >Female Employees

5. Continue….
 Calculated Chi-Square value = 1.8
 Critical Value from the Chart = 3.8
 If calculated Chi-Square value </= the value in chart We can not
reject the null Hypothesis.
 Null Hypothesis Observed = Expected
 Alternate Hypothesis Observed ≠ Expected

6. Test of Independence
To check Two Categorical variables are correlated to each other or
not
Contingency Tables
 Cross tab
 Cross Tabulation Matrix
 Displays the (multivariate) frequency distribution of the
variables.
 It is heavily used in survey research, business intelligence,

7. Steps to find independence of Variables


8. Step 1:
Define Null and Alternate Hypothesis
 Null Hypothesis: NO relation between gender and favorite ruling party.
 If calculated Chi-Square value </= the value in chart. We can not reject
the null Hypothesis.
 Alternate Hypothesis in school: there is relation between gender and
favorite ruling party

9. Why we use the Chi-Square test
Purpose of the Chi-Square test
 The Chi-Square test is used due to the following reasons
 To handle non-numeric data.
 To test the validity of assumptions.
 To apply in a wide range of fields.
 To support decision-making based on Data.
 To compare expected and observed frequencies.
 To identify significant deviations from hypothesis.
 To test relationships between categorical variables.

10. Main reasons for using the test
The key reasons behind using the Chi-Square test are mentioned below
 To test goodness of fit.
 To make evidence-based decisions.
 To handle large sample sizes easily.
 To Identify non-random associations.
 To test the Independence between variables.
 To validate hypotheses in categorical data.

11. Importance
The Chi-Square test has gained importance due to following
reasons
 Simplicity: Easy to calculate and interpret.
 Versatility: Applies to many fields like health, marketing,
and education.
 Objectivity: Replaces guesswork with statistical evidence.
 Non-parametric: Doesn’t assume normal distribution —
great for categorical data.

12. When we use Chi-Square Test
The Chi-square (χ²) test is a widely used non-parametric statistical tool
designed to analyze relationships between categorical variables.
 To test the hypothesis of no association between two or more groups,
population or criteria (i.e. to check independence between two
variables)
 To test how likely the observed distribution of data fits with the
distribution that is expected (i.e., to test the goodness-of-fit)

13. Continue…..
General Criteria for Using the Chi-Square Test:
 You can use the chi-square test when:
 You are working with categorical variables (i.e., data that can be sorted
into groups or categories like gender, preferences, colors, brands).
 You want to compare observed data with expected data based on a
hypothesis or a known distribution.
 You want to check whether two categorical variables are independent.
 There is random sampling from population.
 Expected frequency in each cell should be at least 5 (to ensure accuracy).

14. Continue…
 The Chi-square test is suitable for the following statistical
purposes:
 To determine whether there is a statistically significant
association between two categorical variables.
 To compare the observed distribution of data with an
expected theoretical distribution.
 To test hypotheses about proportional differences in groups
or conditions.

15. Example
If we want to test that in a health camp attended by 50 persons the one
who exercise regularly are having lesser body mass index (BMI) by
taking their actual BMI values, than it cannot be tested using a Chi-
square test. However, if we divide the same set of 50 persons into two
categories as obese with BMI ≥ 30 and nonobese with BMI < 30, than
the same data can be tested using a Chi-square test by counting the
number of obese and nonobese persons across two groups, the one who
exercise regularly and the one who does not. A 2×2 contingency table
also known as cross tables can be constructed for calculating a Chi-
square statistic.

16. When to use a Chi-square Test in the context of
research/data analysis
Life sciences(Botany)
Analyzing Categorical Data
 The Chi-square test is designed for data that falls into categories, such as
plant species, disease resistance, or flower colors.
 It's not appropriate for continuous data like plant height or leaf size, unless
you first categorize the data (e.g., by dividing height into intervals).
Comparing Observed and Expected Frequencies
 You might be observing frequencies of certain traits in a plant population
and want to see if these frequencies align with what you would expect
based on a hypothesis or model.

17. Continue…
 For example, you could use a Chi-square test to compare the
observed number of plants with a certain trait (like disease resistance)
to the expected number based on genetic principles.
Testing for Independence (Association):
 The Chi-square test can also be used to determine if two categorical
variables are related or independent.
 For example, you could use it to see if there's an association between
plant species and their susceptibility to a disease.

18. Where to use Chi-Square test
 The Chi-Square Test used across diverse fields to analyze categorical
data and detect associations or discrepancies between observed and
expected frequencies.
Fields of Application
Life Sciences
 Risk Factor Analysis: Evaluates associations between lifestyle factors
(e.g., smoking) and diseases (e.g., lung cancer) using contingency tables.
 Treatment Comparisons: Tests if different treatments (e.g., drug vs.
placebo) yield significantly different recovery rates.

19. Continue…
 Epidemiology: Assesses disease distribution across populations or
vaccination effectiveness.
 Genetic Studies: Determines if observed trait distributions (e.g., coat
color in animals) align with Mendelian inheritance models
 Ecology: Analyzes species distribution across habitats or
environmental conditions.
 Pollution Studies: Examines associations between industrial activity
and pollution levels in regions

20. Social Sciences and Business
 Public Policy: Analyzes voting patterns, education levels, or
demographic trends to inform policy decisions.
 Curriculum Analysis: Tests if teaching methods (e.g., online vs. in-
person) correlate with student performance
 Consumer Preferences: Tests associations between age groups and
product features (e.g., app color themes)
 Market Research: Evaluates payment method preferences across
product categories (e.g., credit cards vs. PayPal in e-commerce).
 Manufacturing: Verifies if product defects follow a random
distribution or are linked to specific production batches

21. Real-World Examples
 Medical Research: A study tested if COVID-19 vaccination status was
linked to hospitalization rates using a 2x2 contingency table.
 Genetics: Researchers tested if cat litters exhibited expected
genetic trait ratios (e.g., fur color) using observed vs. expected
frequencies.
 Tech Industry: A streaming platform analyzed user preferences for
movie genres and snack purchases to optimize theater inventory.
 Retail: A candy manufacturer used a Goodness-of-Fit Test to verify if
color distributions in candy bags matched advertised claims

22. Software Advancements and Tools
 SPSS: Offers built-in Crosstabs procedures for Chi-Square Tests of
Independence, including expected frequencies and p-values.
 Python/R: Libraries like scipy.stats (Python) and chisq.test() (R) automate
calculations for large datasets
 JMP: Provides interactive visualizations (e.g., clustered bar charts) alongside
test results
 Quantpsy.org: Interactive tools for Goodness-of-Fit and Independence tests
with real-time calculations
 SocSciStatistics: Simplifies Chi-Square computations for contingency tables
up to 5x5.
 Tableau/Power BI: Integrate Chi-Square results into dashboards,
highlighting associations via heatmaps or contingency diagrams.