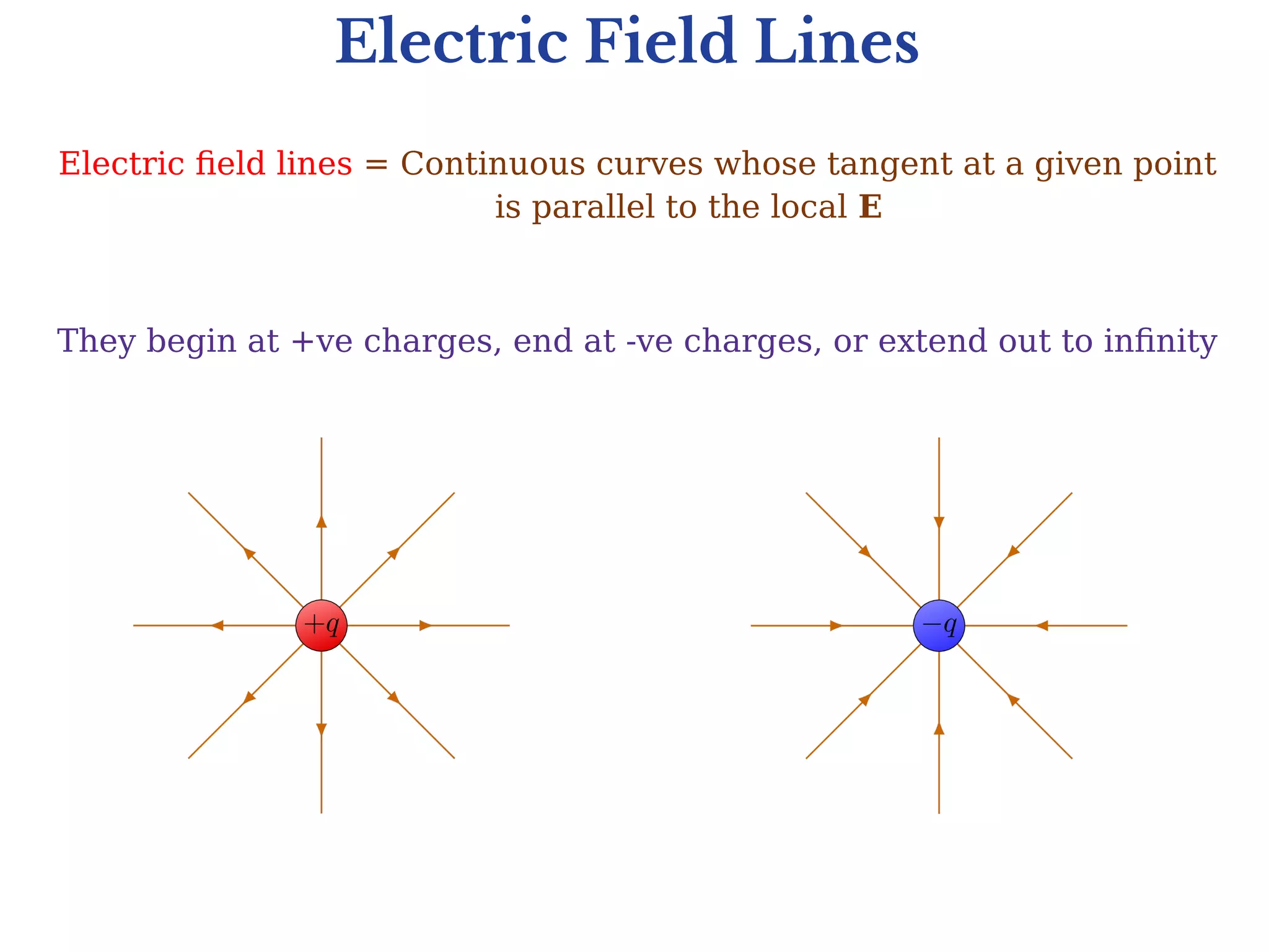
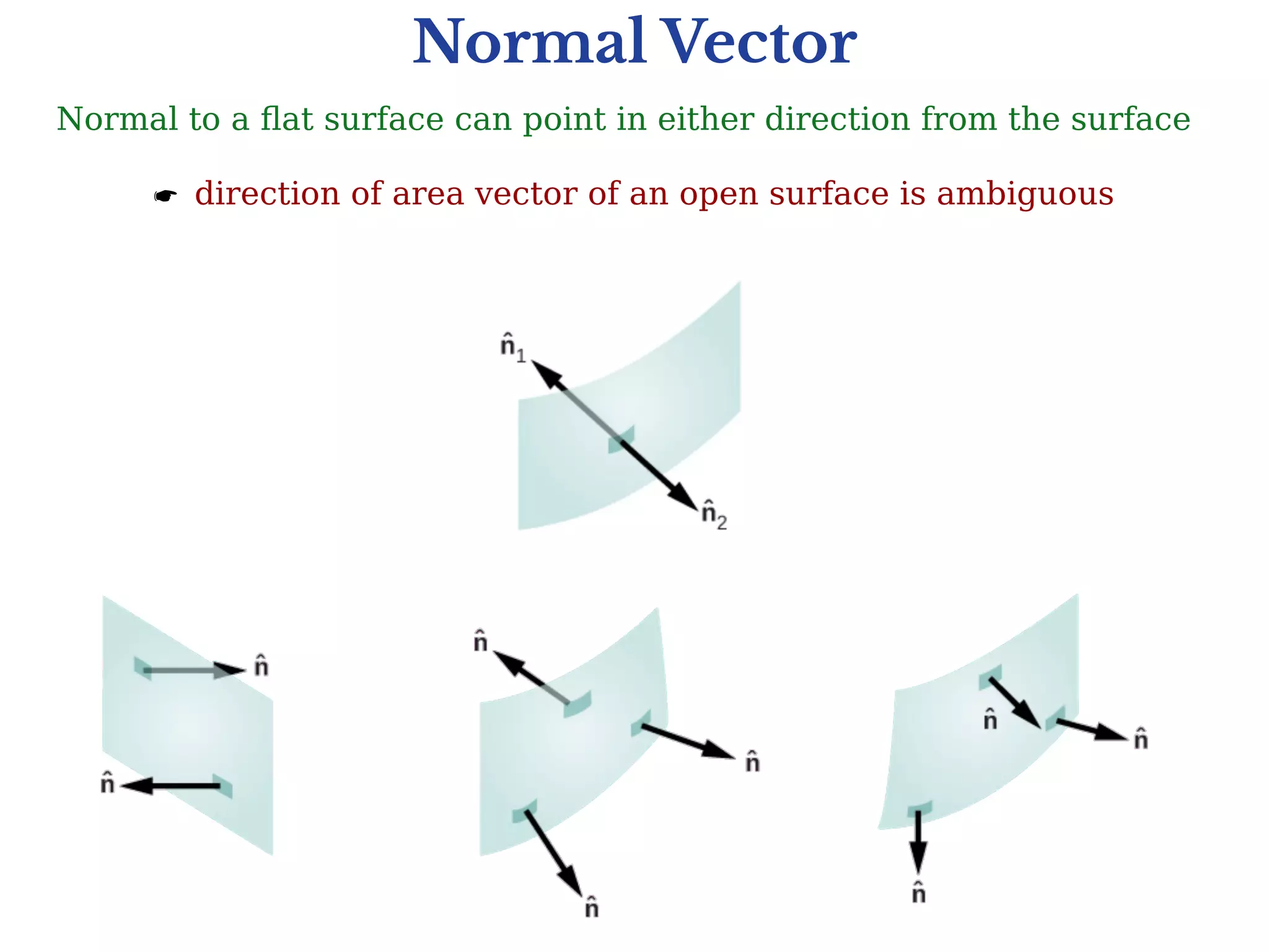
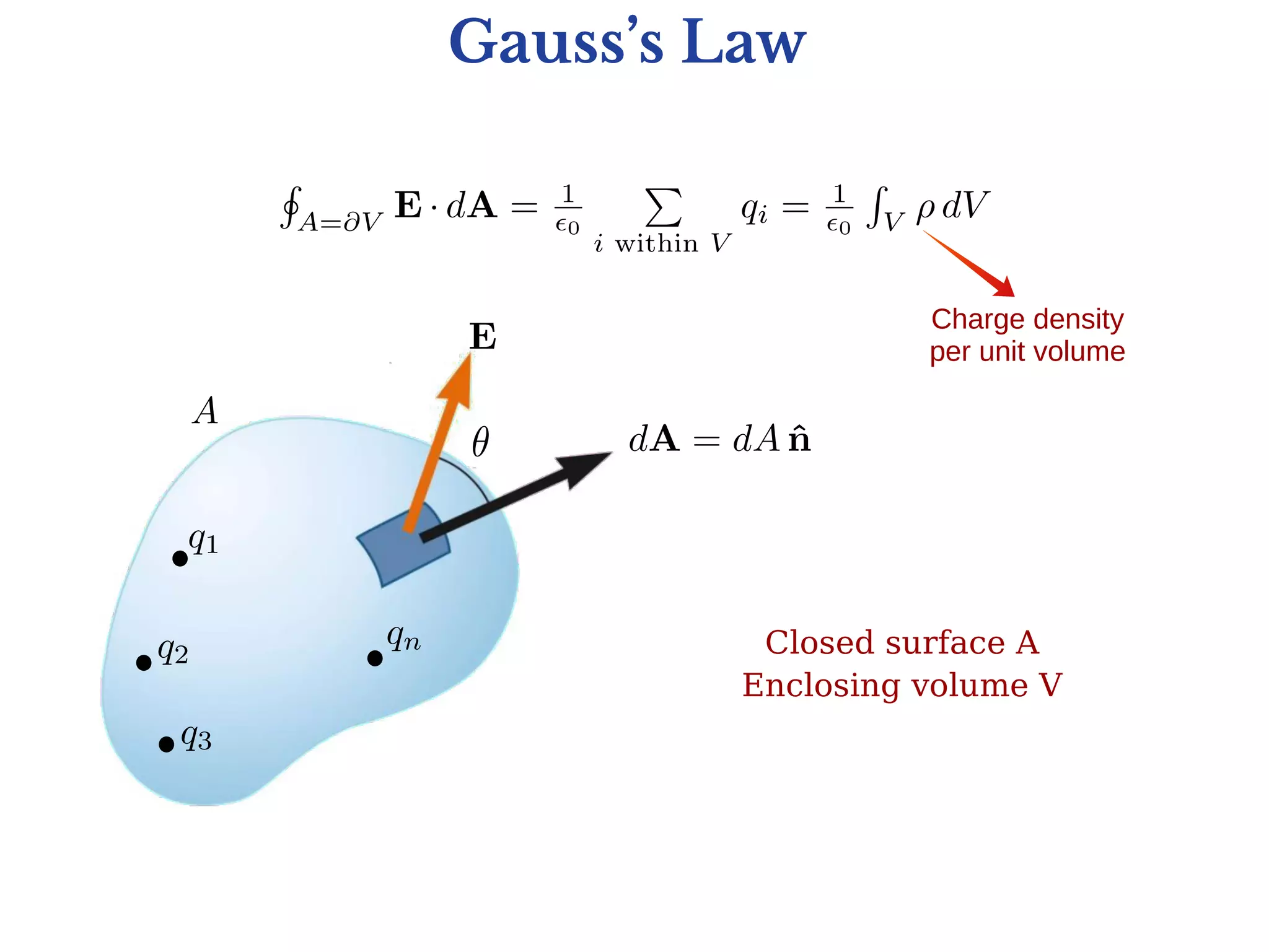
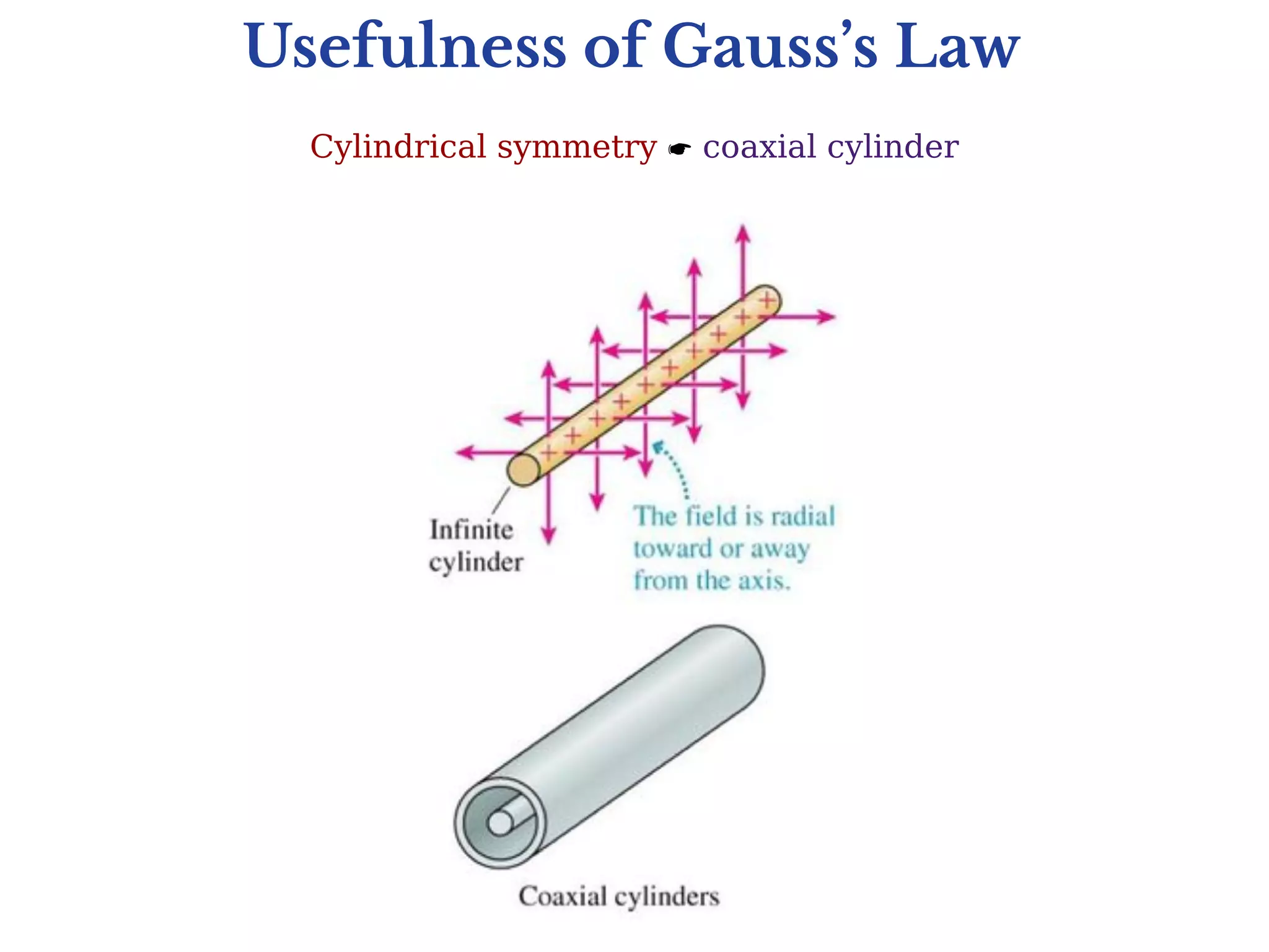
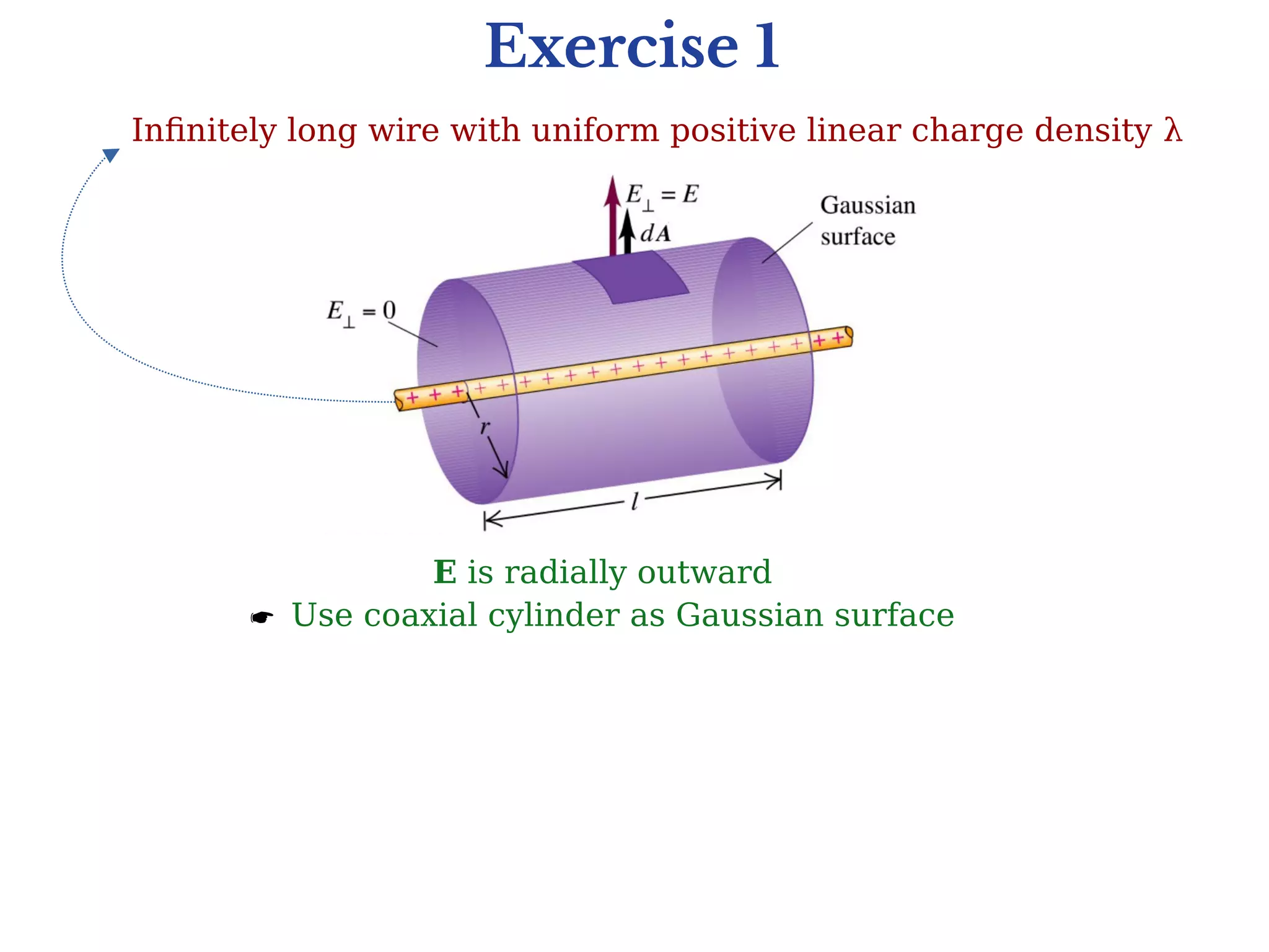
1) Gauss's law relates the electric flux passing through a closed surface to the electric charge enclosed by the surface. It states that the total electric flux passing through any closed surface is equal to 1/ε0 times the net electric charge enclosed, where ε0 is the vacuum permittivity. 2) Gauss's law is useful for calculating electric fields when there is symmetry, such as spherical, cylindrical, or planar symmetry. It allows calculating the electric field due to symmetric charge distributions more easily than using Coulomb's law directly. 3) Applying Gauss's law to conductors in electrostatic equilibrium shows that the electric field inside a conductor must be zero, and any internal cavities will have charge distributed on their

1. Gauss’s Law
Gauss’s Law
Coulomb’s law
Coulomb’s law
expressed differently
expressed differently
Carl Friedrich Gauss

2. Electric Field Vectors
Point charge q at origin
Vector gives E
at a point

3. Electric Field Lines
Connect up the vectors (arrows) to form field lines
Magnitude of field indicated by density of field lines
Electric field lines = Continuous curves whose tangent at a given point
is parallel to the local E

4. Electric Field Lines
Electric field lines = Continuous curves whose tangent at a given point
is parallel to the local E
They begin at +ve charges, end at -ve charges, or extend out to infinity

5. Electric Dipole
Direction of net field E
 tangent to field line
Field is stronger
where lines are denser
Field
line

6. Other Configurations

7. Electric Flux
Electric Flux measures how much electric field
cuts through some arbitrary surface area A
Measure of the "number of field lines" passing through A

8. Electric Flux
Uniform E
Plane perpendicular to E
Electric flux Φ = |E| A

9. Electric Flux
Uniform E
Plane perpendicular to E
Electric flux Φ = |E| A
depends on how
strong E is

10. Electric Flux
Uniform E
Plane perpendicular to E
Electric flux Φ = |E| A
depends on how
strong E is
depends on how
big area is

11. Electric Flux
Uniform E
Plane makes an
angle θ with E
Electric flux Φ = |E| A cos θ

12. Electric Flux
Uniform E
Plane makes an
angle θ with E
depends on how
strong E is
Electric flux Φ = |E| A cos θ
depends on how
big area is
depends on orientation
of the area w.r.t. E

13. Area Vector
Area vector for a planar area element
 magnitude A & direction is perpendicular to plane

14. Electric Flux
Φ = |E| A cos θ = E · A

15. Quick Quiz 1
What is the flux Φ through the plane A?

16. Electric Flux: Generic Case
Although the surface A curves
& E varies (non-uniform)
Flux through a small enough patch
with area vector
is
Total flux through A is

17. Normal Vector
Normal to a flat surface can point in either direction from the surface
 direction of area vector of an open surface is ambiguous

18. Normal Vector
Closed surface
 direction of normal vector at any point on the surface
can be chosen to point from inside to outside

19. Gauss’s Law
Surround a general distribution of charges
by an imaginary closed surface A
Gauss’s law relates the electric field E at all the
points on A to the total charge enclosed within A

20. Gauss’s Law
Closed surface A
Enclosing volume V
Charge density
per unit volume

21. Point Charge at Origin

22. Point Charge at Origin

23. Gauss = Coulomb
Same flux passes through
each of these area elements
Gauss’s law hinges on inverse square nature of E
same number of field lines passes through
any sphere centered at origin,
regardless of size

24. Any Closed Surface
Normal to the surface dA
makes an angle θ with E
Each area elements projects onto
a corresponding
spherical surface element
Total flux through the irregular surface
= total flux through the sphere

25. Principle of Superposition
Gauss = Coulomb
Electric field
for charge qi
Flux through a surface that
encloses all charges {qi}

26. Quick Quiz 2
E through all points on the imaginary surface is
(a) non-zero and uniform
(b) non-zero and non-uniform
(c) zero
Field lines through the
Gaussian surface

27. Usefulness of Gauss’s Law
Gauss's law is always true, but not always useful
When symmetry permits, it affords
quickest + easiest way to compute E
Only 3 kinds of symmetry that work
Spherical
Cylindrical
Planar

28. Usefulness of Gauss’s Law
Spherical symmetry  concentric sphere

29. Usefulness of Gauss’s Law
Cylindrical symmetry  coaxial cylinder

30. Usefulness of Gauss’s Law
Planar symmetry  "pillbox" straddling the surface

31. Exercise 1
E is radially outward
 Use coaxial cylinder as Gaussian surface
Infinitely long wire with uniform positive linear charge density λ

32. Exercise 1
Infinitely long wire with uniform positive linear charge density λ
E is radially outward
 Use coaxial cylinder as Gaussian surface
Area of cylindrical surface = 2 π r l
Flux Φ = 2 π r l |E|
Gauss’s Law  2 π r l |E| = λ l / ϵ0
⇒ |E| = λ / ( 2 π r ϵ0 )

33. Exercise 2
Thin flat infinite sheet with uniform positive surface charge density σ
E ⊥ sheet
 Use Gaussian pillbox

34. Exercise 2
Thin flat infinite sheet with uniform positive surface charge density σ
E ⊥ sheet
 Use Gaussian pillbox
Area of each flat face = A
Flux Φ = 2 |E| A
Gauss’s Law  2 |E| A = σ A / ϵ0
⇒ |E| = σ / (2 ϵ0)

35. References
Chapter 22, University Physics with Modern Physics
by Hugh D. Young & Roger A. Freedman
Sections 2.2.1 - 2.2.3, Introduction to Electrodynamics
by David J. Griffiths

36. Exercise 3
Charge resides entirely on the surface of a solid conductor
in electrostatic equilibrium
Draw a Gaussian surface inside the conductor
 charge enclosed is equal to zero
Gauss’s law  E inside must be zero

37. Exercise 3
Conductor with an internal cavity
E = 0 at all points within the conductor
 E at all points on the Gaussian surface
must be zero
qc

38. Exercise 3
An isolated charge q placed in the cavity
For E to be zero at all points on the Gaussian surface
 surface of the cavity must have a total charge -q
qc+ q