ディープラーニングフレームワークとChainerの実装

ディープラーニングフレームワーク
とChainerの実装
2016/03/07 PPL2016@岡山招待講演
（株）Preferred Networks
奥田遼介

自己紹介
奥田遼介
 -2014東北大学修士
 文字列処理など
 2014 （株）プリファードインフラストラクチャー
 2014- （株）プリファードネットワークス
 映像解析系、製造業系にかかわる研究開発
 ChainerやCuPyの開発
最新v1.7
(2016/3/1)
2/50

何を話すか？
 ディープラーニングの基礎
 ディープラーニングフレームワークの実装
 プログラミングモデル
 記号型と命令型
 Define and RunとDefine by Run
 CuPy：Chainerの裏側を支える技術
 話さない事
 Chainerの使い方、インストール方法
3/50

ディープラーニングの基礎

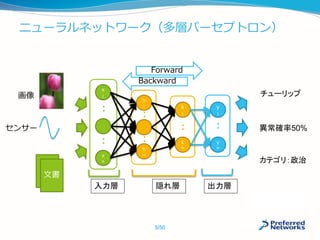
ニューラルネットワーク（多層パーセプトロン）
x
1
x
N
・・ h
1
h
H
・・・・ k
M
k
1
y
M
y
1
Forward
Backward
・・
・・
入力層隠れ層出力層
文書
画像
センサー
チューリップ
異常確率50%
カテゴリ：政治
・・
・・・・
5/50

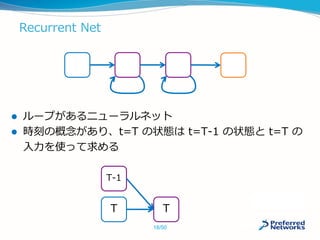
ディープラーニング（DL：DeepLearning）とは
 層が深く、幅も広いニューラルネットワークを利用した
機械学習手法
 2012年の大ブレーク以来、研究コミュニティのみならず
産業界に多く使われてきた
 2014〜2015年中に出された関連論文数は1500を超える*
 画像認識、音声認識などで劇的な精度向上を果たし、その
多くが既に実用化されている
 囲碁でもDeepMindの AlphaGoが大きな成果
 あと40時間でLee Sedol （魔王）と戦う
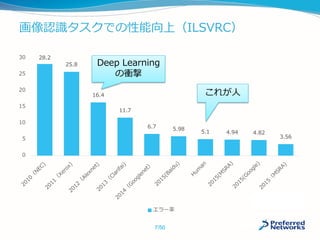
2014年の一般画像認識コンテストで優勝した
22層からなるNNの例 [Google]
*http://memkite.com/deep-learning-bibliography/
2015年の一般画像認識コンテストで優勝した
152層からなるNNの例 [MSRA]
6/50

画像認識タスクでの性能向上（ILSVRC）
28.2
25.8
16.4
11.7
6.7 5.98
5.1 4.94 4.82
3.56
0
5
10
15
20
25
30
エラー率
Deep Learning
の衝撃
これが人
7/50

chainer-DCGAN 学習30分後
画像を0から生成するNN
https://github.com/mattya/chainer-DCGAN
8/50

ニューラルネット
 値が伝播していく有向グラフ
 エッジで重みをかけて、ノードに入るところで足し
込み、ノードの中で非線形変換する
 全体としては巨大で複雑な関数を表す
11/50

ニューラルネット＝合成関数
 ベクトルに対して線形・非線形な関数をたくさん適
用する合成関数と捉えるとよい
 各ノードはベクトルを保持する変数（テンソル）
12/50

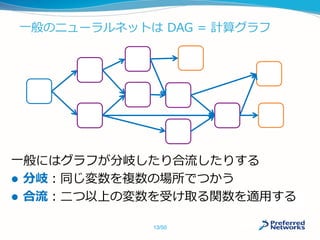
一般のニューラルネットは DAG = 計算グラフ
一般にはグラフが分岐したり合流したりする
 分岐：同じ変数を複数の場所でつかう
 合流：二つ以上の変数を受け取る関数を適用する
13/50

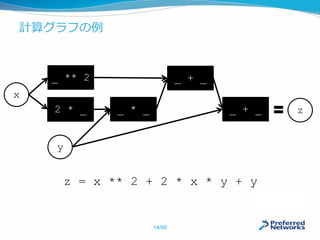
計算グラフの例
z = x ** 2 + 2 * x * y + y
x
y
_ ** 2
2 * _ _ * _ _ + _ z
_ + _
14/50

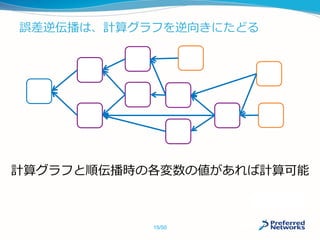
誤差逆伝播は、計算グラフを逆向きにたどる
計算グラフと順伝播時の各変数の値があれば計算可能
15/50

ニューラルネットの学習方法
1. 目的関数の設計
 計算グラフを自分で設計する
2. 勾配の計算
 誤差逆伝播で機械的に計算できる
3. 最小化のための反復計算
 勾配を使って反復更新する
１さえ設計すれば残りは
ほぼ自動化されている
16/50

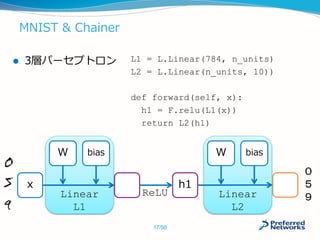
Linear
L2
Linear
L1
MNIST & Chainer
 3層パーセプトロン L1 = L.Linear(784, n_units)
L2 = L.Linear(n_units, 10))
def forward(self, x):
h1 = F.relu(L1(x))
return L2(h1)
ｘ h1
W bias
０
５
９
W bias
ReLU
17/50

Recurrent Net
 ループがあるニューラルネット
 時刻の概念があり、t=T の状態は t=T-1 の状態と t=T の
入力を使って求める
T
T-1
T
18/50

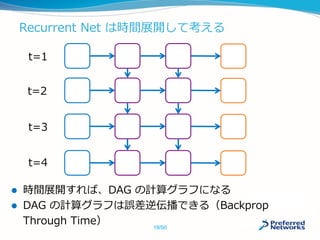
Recurrent Net は時間展開して考える
 時間展開すれば、DAG の計算グラフになる
 DAG の計算グラフは誤差逆伝播できる（Backprop
Through Time）
t=1
t=2
t=3
t=4
19/50

ディープラーニングフレームワークの
実装

フレームワークの構成要素
 いずれも似たような構成要素からなる
 テンソルデータ構造
 変数
 レイヤー（ビルディングブロックとして）
 関数
 ネット
 上の二つをつないだり、たどったり
 最適化ルーチン
 最適化関数（SGDとかAdamとか）
 フレームワークによってこれらの設計指針や抽象化の粒
粒度度、インターフェイスが異なる
21/50

無数にあるディープラーニングフレームワーク
 2015年時点で数十〜数百くらいあるらしい（派生含む）
 注：数え方による
 いろんな会社や団体が作っていてまさに戦国時代
 比較ポイント
 使っている言語：C/C++, Python, R, Matlab, Julia
 機能の充実度：よりけり
 ネットワークの定義の方式：命令型、記号型
 GPUサポート：無し、CUDA、OpenCL
 マルチGPU/ノードサポート：無し、有り
 開発体制：企業、大学、研究機関
22/50

有名なDLフレームワーク比較
主要実装言語 Python C++ Lua Python C++/Python
主要開発者 Preferred
Networks/
Infrastructure
BVLC Idiap Research
Institute,
DeepMind
Univ. of
Montreal
Google
コミュニティ △(日本○) ◎ ○ ○ ○
RNN/LSTM対応 ◎ × ○ ○ ○
動的ネットワー
ク構築
○ × × × ×
拡張性 ○ △ ○ ○ ○
ネットワーク
設計
言語内DSL 設定ファ
イル
(prototxt)
言語内DSL 設定ファイ
ル(YAML)
言語内DSL
（Python）
特徴ネットワーク動
的構築による省
リソース
画像認識
が得意
LuaJITによる
高速化
自動微分機
構
マルチGPU、マル
チノード（gRPC
）をサポート
23/50

記号型（Symbolic）と命令型（Imperative）
 記号型
 記号に対して計算指示を行うこ
とで計算グラフを構築
 Theano, TensorFlow
 設定ファイル型：Caffe, cxxnet
 命令型
 データに対して直接計算を指示
 Chainer
 Torch（本体）, Minerva
#記号型
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# compiles the function
f = compile(D)
d = f(A=numpy.ones(10),
B=numpy.ones(10) * 2)
#命令型
a = numpy.ones(10)
b = numpy.ones(10) * 2
c = b * a
d = c + 1
24/50

記号型が有利：最適化しやすい
 学習ではコンパイル1回に対して実行は複数回
 依存関係解析に長い時間を書けることが可能
 メモリ使用量やマルチGPU、マルチノード最適がしやすい
 不要な値、一時的な値を探しやすい
 例えばTensorFlow では各シンボルは型とサイズを持つ
#記号型
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
A
D
B
B * A + 1
A
B
DC
B * A C + 1
最適化
25/50

命令型が有利：記述の自由度
 プログラミング言語の制御構文を利用して書ける
 複雑な分岐構造や、再帰構造の場合は命令型が有利
a = numpy.ones(10)
c = b * a
d = 0
for i in range(c):
d += c[i] + i
26/50

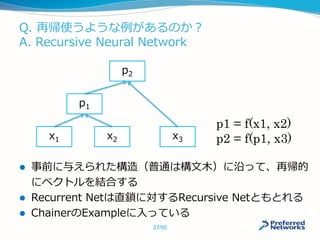
Q. 再帰使うような例があるのか？
A. Recursive Neural Network
 事前に与えられた構造（普通は構文木）に沿って、再帰的
にベクトルを結合する
 Recurrent Netは直鎖に対するRecursive Netともとれる
 ChainerのExampleに入っている
x1 x2
p1
x3
p2
p1 = f(x1, x2)
p2 = f(p1, x3)
27/50

それぞれの欠点はなくせるのか
 命令型：最適化が難しい
 遅延評価する
 過去の実行の演算手順をキャッシュする
 記号型：柔軟性がとぼしい
 がんばってDSLを導入する
 命令型の方針を取り入れる
 向かう先：混ざる
 遅延評価の命令型 or 命令型は記号型に自動変換
 例：MXNet
 デザインノートが充実している
28/50

現在のChainerの仕組み
 Define by Run
 基本的には命令型
 変数に対してbackwardが呼べるように拡張
 つまり、順方向の計算と同時に計算グラフを作る
 Define and Run（対立概念）
 基本的には記号型
 TensorFlow, Theano, Torch nn
a = numpy.ones(10)
c = b * a
d = c + 1
a
b
dc
b * a c + 1
Define by Runで作られる計算グラフ
29/50

なぜDefine by Runを考えたのか？
 より自由にNNを書けるようにするため
 NNの研究を制約しないフレームワークを作る
 可変長、再帰、動的なアテンション
 グラフの途中で値を見て分岐する事もOK
 アイデア
 NNの逆伝播は、順伝播で通った計算の逆で良い
 順伝播を命令型で書けば言語側の制御構文が使える
 命令型で計算グラフを覚える方式
 問題点
 最適化が難しい
30/50

NNフレームワークの現在・今後の課題
 メモリ使用量の削減
 GPUのメモリは小さい（Tesla K80@24GB とても高い）
 150層を超えるような巨大なネットワーク
 長いリカレントネットワーク
 マルチGPU・マルチノード
 どこにどのようなデータを置くか
 どのようなタイミングで転送するか
 自動で最適化しないと使ってもらえない
 ミニバッチをやめたい
 各データ単位で別々のネットワーク構造を使えない
 例：可変長データ、再帰構造データ31/50

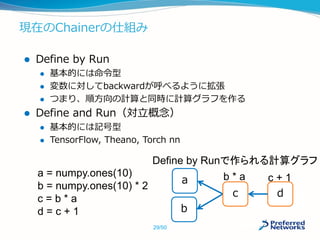
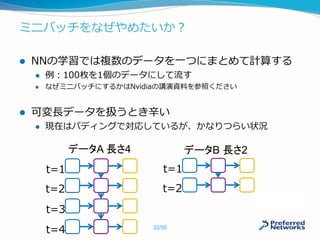
ミニバッチをなぜやめたいか？
 NNの学習では複数のデータを一つにまとめて計算する
 例：100枚を1個のデータにして流す
 なぜミニバッチにするかはNvidiaの講演資料を参照ください
 可変長データを扱うとき辛い
 現在はパディングで対応しているが、かなりつらい状況
t=1
t=2
t=3
t=4
t=1
t=2
データA 長さ4 データB 長さ2
32/50

まとめ
 計算グラフを作るアプローチを説明
 記号型と命令型
 Define and RunとDefine by Run
 最適化と利便性のトレードオフ
 課題
 メモリ使用量の削減
 マルチGPU・マルチノード
 ミニバッチをやめたい
33/50

CuPy：Chainerの裏側を支える技術

CuPyとは何か？
 CUDA上で計算を行うNumPyサブセットのライブラリ
 関数・メソッドのサブセットを実装
 Chainer v1.5.0では約174個の関数が実装済み
 行列積などはcuBLASを利用（高速）
 配列のスライス、転置、reshape 等が自由にできる
 カスタムカーネルの記述も可能
 elementwise, reduction
 Python上で簡単にGPUが使える事を追求
 Python上で簡単に多次元配列といえばNumPy
 PC上で簡単にGPUといえばCUDA
 CUDA＋NumPy ＝CuPy
35/50

どこで使われているのか？
• モデル管理
• 学習ループ抽象化
学習・認識処理
• 自動微分（変数と関数）
• 重みの最適化
計算グラフ処理
• CuPy ← ここ
• Torch(本体), Eigen::Tensor
テンソル計算
• BLAS(OpenBLAS, MKL)
• CUDA(cuBLAS, cuDNN)
行列・畳み込み計算
 DLフレームワークは次のような機能単位で構成される
 かなり雑です。複数の領域にまたがる機能もあります
低
高
36/50

CuPy の使い方は？
 numpy の代わりに cupy を使う（だいたい動く）
 CPU/GPU の両方で動く関数の書き方
 例えば下は NumPy と CuPy の両方で動く logsumexp の実装例
 より省メモリな実装を考えてみてください
def logsumexp(x, axis=None):
xp = cuda.get_array_module(x) #おまじない
x_max = x.max(axis)
exp_sum = xp.exp(x - x_max).sum(axis)
return x_max + xp.log(exp_sum)
37/50

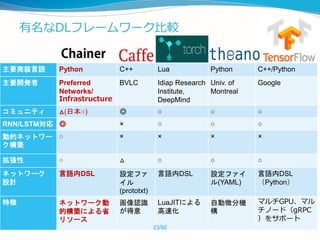
CuPyはどのくらい早いの？
 状況しだいですが、最大数十倍程度速くなります
def test(xp):
a = xp.arange(1000000).reshape(1000, -1)
return a.T * 2
test(numpy)
t1 = datetime.datetime.now()
for i in range(1000):
test(numpy)
print(t2 -t1)
test(cupy)
for i in range(1000):
test(cupy)
print(t2 -t1)
時間
[ms]
倍率
NumPy 2929 1.0
CuPy 585 5.0
CuPy +
Memory Pool
123 23.8
Intel Core i7-4790 @3.60GHz,
32GB, GeForce GTX 970
38/50

CuPyの特徴（1/2）
 Cythonによる高速動作
 PythonはCの200倍遅い
 NumPy準拠のためにいろんな判定が入っている
 NumPy準拠の挙動
 複雑なキャスティングルールも再現（「NumPy闇入門」参照）
 整数8タイプ、浮動小数点数3タイプの計算をサポート
 NumPyお約束のバグも再現
39/50

CuPyの特徴（2/2）
 CUDAコードの動的生成
 対象のテンソルの次元数、データ型に応じてコードを生成
 その場でnvccによるコンパイル（←ここが遅い）
 生成したバイナリはキャッシュされる
 なぜ動的生成するか？
 性能の確保とインストール時間短縮のため
 例えば、加算 A+B=C でもパターン数は３万以上
 次元数0~25：即値を含め 27
 型：整数8、浮動小数3：11^3=1331
 Chainerのテストを全部回すと11595個のカーネルができる
 初回呼び出しは遅い
40/50

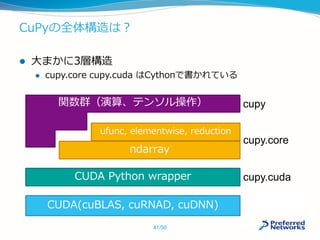
CuPyの全体構造は？
 大まかに3層構造
 cupy.core cupy.cuda はCythonで書かれている
CUDA(cuBLAS, cuRNAD, cuDNN)
ndarray
ufunc, elementwise, reduction
CUDA Python wrapper cupy.cuda
cupy.core
関数群（演算、テンソル操作） cupy
41/50

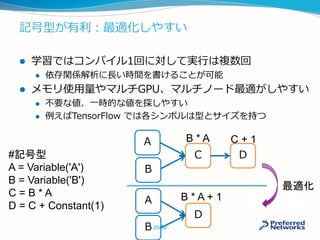
テンソルの実体
 Python側はndarray 、 C++側はCArray
template <typename T, //データ型
int ndim> //次元数
class CArray {
private:
T* data_; //GPUメモリへのポインタ
int size_; //CArray全体の要素数
int shape_[ndim]; //各次元の要素数
int strides_[ndim]; //各次元のストライド
} //不連続な領域を扱うため
42/50

GPU上で計算したい場合
 カーネルをPython中にC++コードで書く
 よく使うものはラップしてある
 ElementwiseKernel
 全要素に同じ計算を行う
 ReductionKernel
 複数要素の集約を計算を行う
 テンソルに対して任意軸（複数）でのReduceが可能
 テンソルのサイズによって２種類の方式を使い分ける
 ufunc
 NumPy互換のElementwise
43/50

ElementwiseKernelの作り方
 要素ごとの2乗誤差をとる関数を定義
 使い方
 ブロードキャストや型チェックは全自動
squared_diff = cupy.ElementwiseKernel(
‘float32 x, float32 y’, #入力
‘float32 z’, #出力
‘z = (x - y) * (x - y)’, #計算
‘squared_diff’) #名前
squared_diff(cupy.arange(10), 10)
44/50

型をジェネリックに扱うことも可能
 1文字の型名はプレースホルダーになる
squared_diff = cupy.ElementwiseKernel(
‘T x, T y’, //入力
‘T z’, //出力
‘z = (x - y) * (x - y)’, //計算
‘squared_diff’) //名前
45/50

Elementwiseカーネルの実体
 Pythonの文字列テンプレートを使って生成
${preamble}
extern "C" __global__ void ${name}(${params})
{
${loop_prep};
CUPY_FOR(i, _ind.size()){ //全要素のループ
_ind.set(i); //インデックスを計算
${operation}; //計算部分
}
${after_loop};
}
46/50

cupy.add(x, y)はどのように実行されるか？
 NumPyのための部分
 引数のオプションを解決（args, kwdargs）
 引数の個数チェック
 引数のdeviceチェック
 引数の型を正規化
 ブロードキャストを実行
 add をどの型の組み合わせで実行するかを解決
 CUDA実行のための部分
 戻り値の割り当て実行
 計算が高速に実行できるように引数を最適化
 CUDAのカーネルコードを生成（キャッシュ付）
 CUDAのカーネル呼び出しのための引数を構築
 カーネル呼び出しを実行 47/50

CuPyの問題点
 細かい単位の関数呼び出しが多くなる
 GPUの帯域律速
 関数合成の仕組みが必要
 非同期呼び出しとメモリプールの相性が悪い
 Malloc, Freeがボトルネックとなるめメモリプールを利用
 現在は一つのストリームのみ使っている
 時々同期する複数ストリームへメモリをどのように割り当てるか？
 その他
 NumPyの関数のカバー率が低い
 Chainerに必要なものから実装中
48/50

まとめ
 ディープラーニングの基礎
 順伝播のみを書く
 逆伝播、最適化は自動化できる
 フレームワークの実装
 数十を超える実装があり、競い合っている
 記号型、命令型に着目した分類とそのトレードオフ
 CuPy
 Chainerをどのように支えているのか
 NumPy準拠はつらい
49/50

参考資料
 MXNet 設計ドキュメント
 Programming Models for Deep Learning
 http://mxnet.readthedocs.org/en/latest/program_model.html
 なぜGPUはディープラーニングに向いているか
 http://www.slideshare.net/NVIDIAJapan/gpu-51812528
 CuPy解説
 http://www.slideshare.net/ryokuta/cupy
 NumPy闇入門
 http://www.slideshare.net/ryokuta/numpy-57587130
We are Hiring!
https://www.preferred-networks.jp/job_ja
50/50

ディープラーニングフレームワーク とChainerの実装

More Related Content

What's hot

Similar to ディープラーニングフレームワーク とChainerの実装