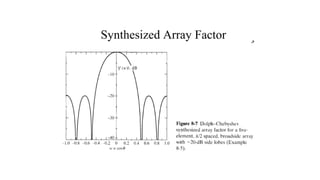
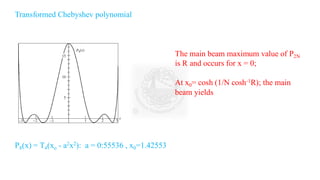
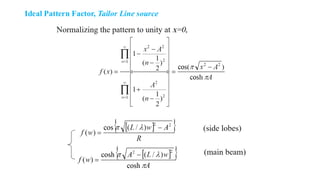
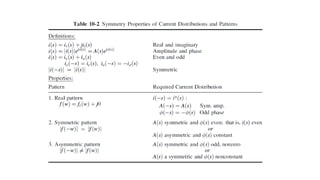
The document discusses antenna synthesis principles and methods, focusing on factors influencing linear arrays and radiation patterns. It outlines mathematical formulations and sampling techniques for synthesizing desired patterns, including methods such as the Woodward–Lawson method and Dolph-Chebyshev approach. The methods aim to optimize antenna performance, notably in achieving low side lobes and narrow main beams for applications in communications and imaging.

1. Department of Studies in Electronics & Communication Engg.,
University B.D.T. College of Engineering
Visveswaraya Technological University, Davanagere-4
Karnataka, India
Dr.T.D. Shashikala
23/7/24

2. MODULE 2
Arrays: Array factor for linear arrays, Uniformly excited equally spaced
linear arrays, Pattern multiplication, Directivity of linear arrays,
Nonuniformly excited equally spaced linear arrays, Mutual coupling.
Antenna Synthesis: Formulation of the synthesis problem, Synthesis
principles, Line sources shaped beam synthesis, Linear array shaped beam
synthesis, Fourier series, Woodward - Lawson sampling method,
Comparison of shaped beam synthesis methods, low side lobe narrow main
beam synthesis methods, Dolph Chebyshev linear array, Taylor line source
method. TEXT(1)

3. Antenna Synthesis

5. ➢ Antenna engineering, has both analysis and synthesis problems
➢ Antenna analysis uses analytical formulation, simulation, and/or
measurement to understand how an antenna operates and to determine
its performance characteristics.
➢ Antenna synthesis is the reverse of analysis: an antenna structure is
derived to meet a given set of performance specifications, most often
the radiation pattern.
➢ Antenna design incorporate analysis or synthesis such as formulating
the electrical and mechanical specifications, selecting the antenna
type, and performing iterative analysis to arrive at an antenna that
meets specifications.

6. Formulation of the Synthesis Problem
A general synthesis procedure would yield the antenna type and its excitation that
produces the best approximation to specified performance values including the desired
pattern shape.

7. ➢ No general synthesis method exists.
➢ Synthesis methods have been developed for each antenna type
➢ Synthesis is divided between continuous and discrete (array) antenna types.
➢ Let f (θ, φ) be the normalized pattern factor, Fd(θ) is the normalized desired radiation
pattern, Then the desired pattern factor is
➢ fd(𝜃) =
𝐹𝑑(𝜃)
𝑠𝑖𝑛𝜃
The normalized pattern factor of a line source along z axis is
f(𝜃) =
1
𝜆
‫׬‬
−𝐿/2
𝐿/2
𝑖 𝑧 𝑒 𝑗𝛽𝑧𝑐𝑜𝑠𝜃 𝑑𝑧;
where i(z) is the normalized form of the current function I(z)
Let w = cos θ, s = z/λ , u= (𝛽𝐿/2)w
f(w) = ‫׬‬
−𝐿/2λ
𝐿/2λ
𝑖 𝑠 𝑒 𝑗2𝜋𝑤𝑠 𝑑𝑠
1. Synthesis Principles

8. i(s) is zero for 𝑠 > L=2/λ, the limits of the integral thus can be extended to infinity,
f(w) = ‫׬‬
−∞
∞
𝑖 𝑠 𝑒 𝑗2𝜋𝑤𝑠 𝑑𝑠 → Fourier transform form ---(1)
i(s) = ‫׬‬
−∞
∞
𝑓 𝑤 𝑒 − 𝑗2𝜋𝑤𝑠 𝑑𝑤 → Inverse Fourier transform ---(2)
➢ The current distribution and the pattern functions can be described mathematically in
terms of either real and imaginary, or amplitude and phase, or even and odd parts, as
shown in the definitions section of Table 10-2
➢ The pattern properties and the associated required current distribution in Table 10-2 are
explained next.

10. 1. Synthesis Property 1:
A real-valued pattern is achieved if and only if the current distribution amplitude is
symmetric and the phase is odd.
2. Synthesis Property 2:
A real-valued current distribution produces a symmetric pattern.
3. Synthesis Property 3:
An asymmetric pattern can be realized only through the use of current phase control.

11. 2. LINE SOURCE SHAPED BEAM SYNTHESIS METHODS
➢ The main beam of an antenna pattern is required to be a specified shape
➢ One-dimensional continuous current distributions (i.e., line sources)
1. The Fourier Transform Method
From eqns 1 & 2, for the desired pattern fd(w), the corresponding direct current
distribution is
id(s) = ‫׬‬
−∞
∞
𝑓𝑑 𝑤 𝑒 − 𝑗2𝜋𝑤𝑠 𝑑𝑤
In general id(s) is confined to 𝑠 ≤ 𝐿/2λ, hence an approximate solution of this gives a
synthesized current distribution is,
i(s)= ቐ
id(s) 𝑠 ≤ 𝐿/2λ
0 𝑠 >
𝐿
2λ
The current i(s) produces an approximate pattern f (w)
The current id(s) extending over all S produces the pattern fd(w) exactly.

12. The Fourier transform synthesized pattern yields the least mean-square error (MSE),
MSE= ‫׬‬
−∞
∞
𝑓 𝑤 − 𝑓𝑑(𝑤) dw ; f(w) corresponding to i(s), the smallest pattern
Refer to EXAMPLE 10-1
A particularly convenient way to synthesize a radiation pattern is to specify values of the
pattern at various points, that is, to sample the pattern.
2. The Woodward–Lawson Sampling Method
➢ It is based on the decomposition of the source current distribution into a sum of uniform
amplitude, linear phase sources
➢ in(s) =
𝑎𝑛
𝐿/λ
e -j2𝛑wns , 𝑠 ≤ 𝐿/2λ
➢ The pattern corresponding to this component current
➢ fn(w)= an Sa 𝜋
𝐿
λ
(𝑤 − 𝑤𝑛) ;
➢ Sa(x)= sin(x)/x , the sampling function,
➢ an & wn current component amplitude & phase coefficients

14. In the Woodward–Lawson method, the total current excitation is composed of a sum of
2M+1 component currents as
i(s)= σ𝑛=−𝑀
𝑀
𝑖𝑛(𝑥) =
1
𝐿/λ
σ𝑛=−𝑀
𝑀
𝑎𝑛e −j2𝛑wns ; where wn=
𝑛
𝐿/λ
, 𝑛 ≤ 𝑀, 𝑤𝑛 ≤ 1.0
➢ The pattern corresponding to this current is
f(w)= σ𝑛=−𝑀
𝑀
𝑓𝑛(𝑤) ; where fn(w) = an Sa 𝜋
𝐿
λ
(𝑤 − 𝑤𝑛)
= σ𝑛=−𝑀
𝑀
an Sa 𝜋(
𝐿
λ
𝑤 − 𝑤𝑛) ;
➢ At pattern points w = wn = n𝜆 /L, this reduces to f(w = wn)= an ;
➢ an→ pattern sample values at wn → pattern sample points

16. 3. LINEAR ARRAY-SHAPED BEAM SYNTHESIS METHODS
➢ Consider an equally spaced linear array along the z-axis with interelement
spacing d.
➢ The physical center of the array is located at the origin
➢ The total number of elements in the array P can be either even (then let P =
2N) or odd (then let P = 2N +1)
➢ The total array length is L=Pd

17. For an odd element number,
1. The element locations are given by Zm= md, 𝑚 ≤ 𝑁 ; P = 2N+1
2. Array Factor f(w) = σ𝑚=−𝑁
𝑁
𝑖𝑚e j2𝛑m(d/λ)w ; im=element currents
For an even element number,
1. Zm=
2𝑚−1
2
.d , 1≤ 𝑚 ≤ 𝑁 ; & Z-m=
2𝑚−1
2
.d , -N≤ 𝑚 ≤ 1 ; P=2N
2. Array Factor
f(w) = σ𝑚=1
𝑁
(𝑖−m e −j𝛑(2m−1)(d/λ)w + 𝑖m e j𝛑(2m−1)(d/λ)w )

18. 1. The Fourier Series Method
➢ The array factor resulting from an array of identical discrete radiators
➢ The sum over the currents for each element weighted by the spatial phase delay from
each element to the far-field
➢ The desired pattern in the interval −
λ
𝟐𝒅
< 𝑤 <
λ
𝟐𝒅
fd(w) = σ𝑚=−∞
∞
𝑏𝑚e j2𝛑m(d/λ)w ;
where bm =
𝑑
λ
‫׬‬
−
λ
𝟐𝒅
λ
𝟐𝒅
𝑓𝑑 𝑤 𝑒 − 𝑗2𝜋m(d/λ)𝑤 ; 𝑑𝑤 → element currents

19. ➢ The practical AF for finite elements is
f(w) = σ𝑚=−𝑁
𝑁
𝑏𝑚e j2𝛑m(d/λ)w
➢ Let im=bm , 𝑚 ≤N, → the element excitation currents equal to Fourier series
coefficients bm calculated from the desired pattern fd
The array factor f arising from these element currents is an approximation to the desired
pattern and provides the least mean-squared error
The synthesized pattern;
f(w) = σ𝑚=1
𝑁
(𝑖−me −j𝛑(2m−1)(d/λ)w + 𝑖me j𝛑(2m−1)(d/λ)w )
With currents im= bm and i-m= b-m

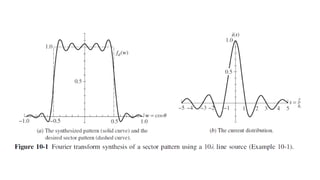
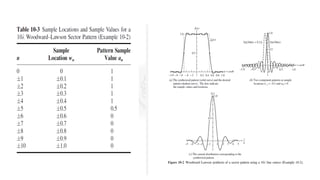
20. 2. Woodward–Lawson Sampling Method
➢ This method is analogous to Woodward–Lawson sampling method for line sources
➢ The synthesized array factor is the superposition of array factors from uniform
amplitude, linear phase arrays
➢ f(w)=σ𝑛=−𝑀
𝑀
𝑎𝑛
sin[
𝑝
2
𝑤−𝑤𝑛
2𝛑
λ
𝑑]
P sin[
1
2
𝑤−𝑤𝑛
2𝛑
λ
𝑑]
➢ where the sample values are an= fd(w=wn); & wn= n (
λ
𝑃𝑑
) =
𝑛
𝑙/λ
, 𝑛 ≤ 𝑀, 𝑤𝑛 ≤1.0
➢ The element currents required to give this pattern are
im =(1/p) σ𝑛=−𝑀
𝑀
𝑎𝑛e −j2𝛑(Zm/λ)wn → for either even or odd elements

22. 3. Comparison of Shaped Beam Synthesis Method
➢ Three distinct types of pattern regions: side lobe, main beam, and transition
➢ Over the side lobe region, SLL is defined as
SLL= 20 log
𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑡ℎ𝑒 ℎ𝑖𝑔ℎ𝑒𝑠𝑡 𝑠𝑖𝑑𝑒 𝑙𝑜𝑏𝑒 𝑝𝑒𝑎𝑘
max 𝑜𝑓 𝑑𝑒𝑠𝑖𝑟𝑒𝑑 𝑝𝑎𝑡𝑡𝑒𝑟𝑚
➢ Over the main lobe region the measure of Ripple R is
R = 20 max log
𝑓(𝑤)
𝑓𝑑(𝑤)
[db]
➢ The Transition width T, which gives a measure of fall of main beam in side
lobe region is T = 𝑤𝑓 = 0.9 −
𝑤𝑓 = 0.1 ;
➢ 𝑤𝑓=0.9 & 𝑤𝑓=0.1 are discontinuity in the desired pattern at w=90 & 10 %
The shaped beam synthesis methods can be compared easily using
SLL, R, and T.
➢ The Woodward–
Lawson methods
produce low side
lobes and low
main beam
ripple at some
sacrifice in
transition width.
➢ Fourier methods
yield somewhat
inferior side lobe
levels, ripples
&small
transition width

24. 4. LOW SIDE LOBE, NARROW MAIN BEAM SYNTHESIS METHODS
➢ Point-to-point communications and imaging
➢ Single narrow beam and low side lobes to reject unwanted signals in directions outside
the main beam
➢ Extreme side lobe reduction is used to cope with high-power jamming transmitters.
➢ Dynamic (adaptive) pattern control is required to counter interference or jamming signals
that change arrival direction.
Two most popular methods to synthesize narrow beam, low side lobe patterns
1. Dolph-Chebyshev method for linear arrays
2. Taylor line source method

25. 1. The Dolph-Chebyshev Linear Array Method
Method for achieving the optimum broadside linear array with equal element spacings that are equal
to or greater than a half-wavelength
➢ A uniform line source has a first side lobe level of 13.3 dB
➢ A uniform linear array has slightly higher side lobes and depends on the number of elements.
➢ The side lobes lower as the element current amplitude taper from the center to the edge of an array is
increased
1. Chebyshev polynomials
➢ the Chebyshev polynomials help to determine the optimal excitation coefficients
➢ have equal ripples. Optimum side lobe performance occurs when side lobes of equal level
2. Dolph applied Chebyshev polynomials in this manner to arrays

27. Important general properties of Chebyshev polynomials
1. The even-ordered polynomials are even, that is, Tn( - x) =Tn(x) for n
even, and the odd-ordered ones are odd, that is, Tn( - x)= - Tn(x); for
n odd.
2. All polynomials pass through the point (1, 1). In the range -1 ≤ x ≤ 1
3. All zeros (roots) of the polynomials also lie in -1 ≤ x ≤ 1
The equal amplitude oscillations of Chebyshev polynomials in the region
𝑥 ≤ 1 is the desired property for equal side lobes.
Also, the polynomial nature of the functions makes
them suitable for array factors since an array factor can be written as a
polynomial.

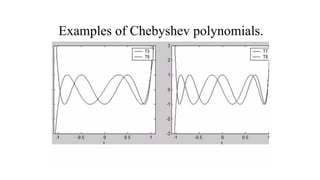
30. Symmetrically Excited, Broadside Array
➢ i-m= im ; zm=md, &
➢ i0 is at origin (z = 0), ψ= 2𝜋(d/λ)𝑤
➢ f(ψ) = ቐ
𝑖0 + 2 σ𝑚=1
𝑁
𝑖𝑚𝑐𝑜𝑠𝑚ψ 𝑃 𝑜𝑑𝑑
2 σ𝑚=1
𝑁
𝑖𝑚𝑐𝑜𝑠[
2𝑚−1 ψ
2
]
P even
➢ Using trigonometric identities, cos(mψ) = σ𝑚=1
𝑁
𝑐𝑜𝑠[
ψ
2
])
➢ Let x= x0cos ψ/2 then f(ψ) = Tp-1(x0cos ψ/2 ) ;
➢ 𝜃 = 900 → a broadside array.
Chebyshev polynomial T4(x)

31. R is main beam-to-side lobe ratio; xo at the main beam maximum, P array elements

32. Beam width and Directivity
HP = 𝛑 – 2 cos-1 ψ
𝛽𝑑
broadside ; HP= 2 cos-1 ψℎ
𝛽𝑑
endfire
The directivity of Dolph-Chebyshev arrays
D ≈
𝟐𝑹𝟐
𝟏+𝑹𝟐
𝑯𝑷
; broadside --(1)
EXAMPLE 10-5
The directivity for equi-phased, half-wavelength spaced
10 element -30db SL array
D=
σ𝑚=−2
2 𝑖𝑚
2
σ𝑚=−2
2 𝑖𝑚
2 = 4.69 (10 element UELA) ;
D=4.72 from Dolph-Chebyshev(1)

34. 2. The Taylor Line Source Method
➢ Dolph-Chebyshev array does yield the highest directivity and narrowest beamwidth
➢ Optimum narrow beam pattern from a line source antenna occurs when all side lobes
are of equal level
➢ The Chebyshev polynomial TN(x) has N-1 equal level “side lobes” in the region -1<X<
1, and for 𝑥 > 1, its magnitude increases monotonically
➢ A change of variables will transform the Chebyshev polynomial into the desired pattern
form; that is, with a zero-slope main beam maximum at x=0 and equal level side lobes.

35. The new function resulting from the variable change

36. Transformed Chebyshev polynomial
P8(x) = T4(xo - a2x2): a = 0:55536 , x0=1.42553
The main beam maximum value of P2N
is R and occurs for x = 0;
At x0= cosh (1/N cosh-1R); the main
beam yields

37. Nulls of the Array Factor

38. Selection Of Constant A

39. Ideal Pattern Factor, Tailor Line source

40. Realistic Pattern Factor, Approximate Tailor Line source

41. The Taylor
line source
is actually a
pattern of
the Wood
ward–
Lawson
family.
The Woodward Lawson Equivalent

42. Beam width and Directivity

43. Refer EXAMPLE 10-7