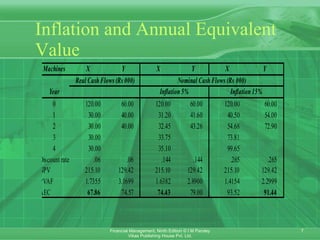
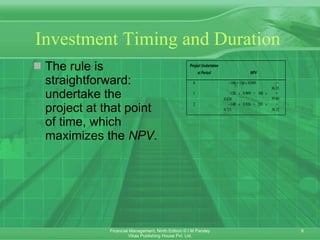
This document discusses complex investment decisions involving projects with different lives, replacement decisions, and capital rationing. It provides methods for evaluating mutually exclusive projects over equal periods using annual equivalent value (AEV). Under capital rationing, where funds are limited, the profitability index method ranks projects by NPV per rupee invested, but other techniques like linear programming may be needed for multi-period constraints or indivisible projects. Replacement decisions are made by comparing the AEV of old and new assets.

1. Chapter - 11 Complex Investment Decisions

2. Chapter Objectives Show the application of the NPV rule in the choice between mutually exclusive projects, replacement decisions, projects with different lives etc. Understand the impact of inflation on mutually exclusive projects with unequal lives. Make choice between investments under capital rationing. Illustrate the use of linear programming under capital rationing situation.

3. Complex Investment Problems How shall choice be made between investments with different lives? Should a firm make investment now, or should it wait and invest later? When should an existing asset be replaced? How shall choice be made between investments under capital rationing?

4. Projects with Different Lives The choice between projects with different lives should be made by evaluating them for equal periods of time .

5. Annual Equivalent Value (AEV) Method The method for handling the choice of the mutually exclusive projects with different lives, as discussed in last slide, can become quite cumbersome if the projects’ lives are very long. We can calculate the annual equivalent value (AEV) of cash flows of each project. We shall select the project that has lower annual equivalent cost .

6. AEV for Perpetuities When we assume that projects can be replicated at constant scale indefinitely, we imply that an annuity is paid at the end of every n years starting from the first period. where NPV  is the present value of the investment indefinitely, NPV n is the present value of the investment for the original life, n and k is the opportunity cost of capital.

7. Inflation and Annual Equivalent Value

8. Investment Timing and Duration The rule is straightforward: undertake the project at that point of time, which maximizes the NPV .

9. Tree Harvesting Problem The maximisation of the investment’s NPV would depend on when we harvest trees. The net future value of trees increases when harvesting is postponed; but the opportunity cost of capital is incurred by not realising the value by harvesting the trees. The NPV will be maximised when the trees are harvested at the point where the percentage increase in value equals the opportunity cost of capital. Suppose the net future value obtained over the years from harvesting the trees is A t and if the opportunity cost of capital is k , then the net present value (NPV) of the net realisable value of trees is given by:

10. Tree Harvesting Problem To determine the optimum harvesting time, which maximizes the NPV, we set the derivative of the NPV with respect to t in Equation equal to zero. Land may have value since the trees can be replanted. Therefore, the correct formulation of the problem will be to assume that once the trees are harvested, the land will be replanted. Thus, if we consider a constant replication of the tree-harvesting investment indefinitely, then the NPV will:

11. Replacement of an Existing Asset Compare the annual equivalent value (AEV) of the old and new equipment as given below. It is indicated that a chain of new machines is equivalent to an annuity of Rs 9,630  3.605 = Rs 2,671 a year for the life of the chain. The existing machine is still capable of providing an annuity of: Rs 7,390  2.402 = Rs 3,076. So long as the existing machine generates a cash inflow of more than Rs 2,671 there does not seem to be an economic justification for replacing it.

12. Investment Decisions Under Capital Rationing Capital rationing refers to a situation where the firm is constrained for external, or self-imposed, reasons to obtain necessary funds to invest in all investment projects with positive NPV. Under capital rationing, the management has not simply to determine the profitable investment opportunities, but it has also to decide to obtain that combination of the profitable projects which yields highest NPV within the available funds.

13. Why Capital Rationing There are two types of capital rationing: External capital rationing. Internal capital rationing.

14. Profitability Index The NPV rule should be modified while choosing among projects under capital constraint. The objective should be to maximise NPV per rupee of capital rather than to maximise NPV. Projects should be ranked by their profitability index, and top-ranked projects should be undertaken until funds are exhausted. The Profitability Index does not always work. It fails in two situations: Multi-period capital constraints. Project indivisibility.

15. Programming Approach to Capital Rationing Linear Programming (LP) Integer Programming (IP) Dual variable