Download to read offline
Uploaded byAntonio Vallecillo
Introducing Subjective Knowledge Graphs
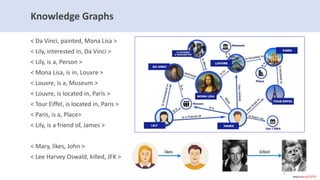
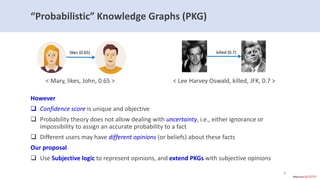
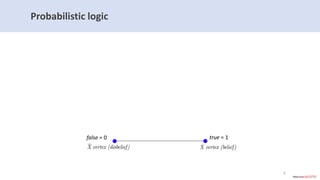
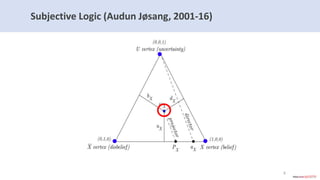
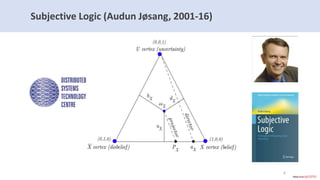
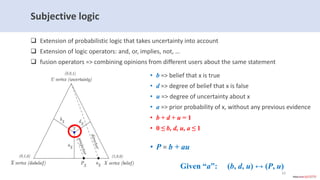
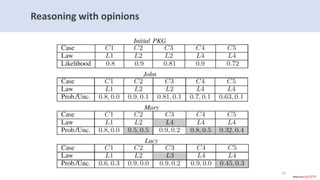
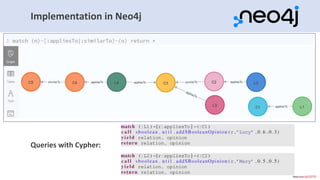
The document introduces subjective knowledge graphs which extend probabilistic knowledge graphs (PKGs) by incorporating subjective opinions to account for uncertainty and varying user beliefs. It discusses the application of subjective logic, including operators for fusing different opinions, and presents methods for reaching consensus among users. The evaluation of this approach is demonstrated through its implementation in Neo4j, highlighting scalability and performance with various future research directions.
More Related Content
Similar to Introducing Subjective Knowledge Graphs
![谷歌留痕技术教程[ 𝙩𝙤𝙥 𝟮𝟯𝟯. 𝙘 𝙤𝙢 ]](https://cdn.slidesharecdn.com/ss_thumbnails/top233-260130173900-2eb784f9-thumbnail.jpg?width=640&height=640&fit=bounds)
Introducing Subjective Knowledge Graphs
- 1. Introducing Subjective KnowledgeGraphs Francisco J. Navarrete and Antonio Vallecillo ITIS Software, Universidad de Málaga, Spain
- 2. Knowledge Graphs < DaVinci, painted, Mona Lisa > < Lily, interested in, Da Vinci > < Lily, is a, Person > < Mona Lisa, is in, Louvre > < Louvre, is a, Museum > < Louvre, is located in, Paris > < Tour Eiffel, is located in, Paris > < Paris, is a, Place> < Lily, is a friend of, James > < Mary, likes, John > < Lee Harvey Oswald, killed, JFK > killed likes 2
- 3. “Probabilistic” Knowledge Graphs(PKG) < Mary, likes, John, 0.65 > < Lee Harvey Oswald, killed, JFK, 0.7 > killed (0.7) likes (0.65) 3
- 4. “Probabilistic” Knowledge Graphs(PKG) < Mary, likes, John, 0.65 > < Lee Harvey Oswald, killed, JFK, 0.7 > However Confidence score is unique and objective Probability theory does not allow dealing with uncertainty, i.e., either ignorance or impossibility to assign an accurate probability to a fact Different users may have different opinions (or beliefs) about these facts Our proposal Use Subjective logic to represent opinions, and extend PKGs with subjective opinions killed (0.7) likes (0.65) 4
- 5. Boolean Logic false =0 true = 1 5
- 6. Probabilistic logic false =0 true = 1 6
- 7.
- 8. Subjective Logic (AudunJøsang, 2001-16) 8
- 9. Subjective Logic (AudunJøsang, 2001-16) 9
- 10. Subjective logic Extensionof probabilistic logic that takes uncertainty into account Extension of logic operators: and, or, implies, not, … fusion operators => combining opinions from different users about the same statement • b => belief that x is true • d => degree of belief that x is false • u => degree of uncertainty about x • a => prior probability of x, without any previous evidence • b + d + u = 1 • 0 ≤ b, d, u, a ≤ 1 • P = b + au Given “a”: (b, d, u) ↔ (P, u) 10
- 11. Different people canexpress their subjective opinions < Oct 11, rains, Brisbane, 0.65 > < Oct 12, rains, Brisbane, 0.68 > < Oct 13, rains, Brisbane, 0.59 > < Oct 14, rains, Brisbane, 0.40 > < Oct 15, rains, Brisbane, 0.40 > < Oct 16, rains, Brisbane, 0.0 > (0.3,0.6,0.1,0.59); P=0.36 (0.4,0.1,0.5,0.59); P=0.7 (0.59,0.11,0.3,0.59); P=0.77 11
- 12. Extending PKGs toSKGs A PKG about Laws (L) that can be applied to legal cases (C) < L1, appliesTo, C1, 0.8 > < L2, appliesTo, C2, 0.9 > < L3, appliesTo, C3, 0.7 > < L4, appliesTo, C3, 0.6 > < L4, appliesTo, C4, 0.9 > < C2, similarTo, C3, 0.9 > < C4, similarTo, C5, 0.8 > 12
- 13. “Subjective” Knowledge Graphs <L1, appliesTo, C1, 0.8, {(Lucy; 0.6, 0.3)} > < L2, appliesTo, C2, 0.9, {(Mary; 0.5, 0.5), (John; 0.9, 0.1)} > < L3, appliesTo, C3, 0.7, {(Mary; 0.6, 0.5), (Lucy; 0.9, 0.2), (John; 0.8, 0.1)} > < L4, appliesTo, C3, 0.6, {(Mary; 0.9, 0.2), (Lucy; 0.7, 0.2), (John; 0.4, 0.6)} > < L4, appliesTo, C4, 0.9, {(Mary; 0.8, 0.5), (John; 0.7, 0.1)} > < C2, similarTo, C3, 0.9, {(Lucy; 0.7, 0.3), (John; 0.9, 0.1)} > < C4, similarTo, C5, 0.8, {(Mary; 0.4, 0.5), (Lucy; 0.5, 0.5) , (John; 0.9, 0.1)} > 13 Mary John Lucy
- 14.
- 15. Reaching consensus Usingthe Average Belief Fusion operator in this case 15
- 16. Implementation in Neo4j Querieswith Cypher: 16
- 17. Reasoning with subjectiveopinions 17
- 18. Evaluation and futurework Evaluation: Scalability and performance Probabilistic Knowledge Graph from NELL • 2.12 Million nodes and 644,899 relations and associated confidence scores Different queries using our neo4j implementation • Results in the order of milliseconds (as in NELL) Added subjective opinions from different belief agents • Responses between 1.28 and 1.6 times the original ones Further issues (to be investigated as part of future work) Use of Subjective logic by domain experts (usability, correctness) Representation of individual opinions • (a) Subjective opinions; (b) projections + uncertainty, or (c) Likhert scales (probably, possibly, unlikely) Temporal validity of opinions Correlated facts Further case studies and applications 18
- 19. Introducing Subjective KnowledgeGraphs Francisco J. Navarrete and Antonio Vallecillo ITIS Software, Universidad de Málaga, Spain
Editor's Notes
- #2 Good morning. This work introduces Subjective Knowledge graphs, and has been developed by Francisco Navarrete and Antonio Vallecillo, from the University of Malaga, Spain.
- #3 Let’s start by remembering that Knowledge Graphs provide structured representation of real-world entities and relations in the form of the so-called Subject-Predicate-Object triples that describe facts. Examples of these triples are “Da Vinci painted Mona Lisa”, “Tour Eiffel is located in Paris”, or “Mary Likes John”. They are used by search engines such as Google, Bing, or Yahoo; knowledge-engines and question-answering services Apple's Siri, and Amazon Alexa; and by social networks such as LinkedIn or Facebook.
- #4 Since knowledge is not free from uncertainty, Probabilistic Knowledge Graphs associate a “confidence score” to each triple, which is a weight that represents the likelihood of the fact or the intensity of the relationship represented by the triple. Normally, probabilities are used to represent confidence scores. For example “Mary likes John with a confidence score of 0.65”, or “Lee Harvey Oswald killed JFK with a probability of 0.7”.
- #5 However, sometimes assigning a probability to a fact is difficult because there is always a related uncertainty. Besides, two users may have different opinions about the same fact, and could assign different confidence scores to it. Standard probability falls short for addressing these issues, and this is where Subjective Logic comes into play.
- #6 To understand subjective logic and its power, let’s start first by classical Boolean logic, where you only have true and false (or 1 and 0) to represent, respectively, belief and disbelief on a given fact.
- #7 Probabilistic logic extends Boolean logic by being able to assign a degree of belief to a fact, by means of a number between 0 and 1. However, this approach cannot capture uncertainty.
- #8 Kleene logic helps here, defining three discrete values: true, false, and don’t know. However, no degrees of belief or disbelief can be captured.
- #9 Subjective logic embraces and extends these approaches by assigning a degree of belief, a degree of disbelief, and a degree of uncertainty to each opinion.
- #10 There is a whole theory about subjective logic, which, interestingly, was developed by Audun Josang partly here in Brisbane during his stay at the DSTC in early 2000!
- #11 In addition to extending the traditional Boolean operators “and”, “or”, “implies”, “not”, etc., this logic allows different users to express different opinions. It also provides operators to combine these opinions in order to reach consensus (the so-called “fusion” operators). A subjective opinion is formed by a tuple composed of a degree of belief, a degree of disbelief, a degree of uncertainty, and the prior probability over which the opinion is made. Being an extension of Probabilistic logic, probabilities can be lifted to subjective opinions, and also subjective opinions can be projected into probabilities. The projection operation P is used for this. P equals b plus a times u. Something that we will later use is the fact that, given a prior probability “a”, users can express their opinions either by stating their degrees of belief, disbelief and uncertainty, or by simply stating their projected (or posterior) probability and the degree of uncertainty. We realized that sometimes this is much easier for users.
- #12 For example, consider the common case of a weather forecast service. Given a prior probability of 59 % chances of rain in Brisbane on Wednesday, three people can express different opinions, depending on how much they trust the weather forecasting service. The three users are able to express their degrees of uncertainty, while the projected probability reflects the new chances of rain each one expects. This is precisely how we propose to extend probabilistic knowledge graphs, in order to build subjective knowledge graphs
- #13 To illustrate our proposal, the following example shows a Probabilistic Knowledge Graph with laws that can be applied to legal cases C1 to C5. Some legal cases can be considered somehow similar, with a given confidence score, and therefore other laws can be applied to them too. The standard reasoning mechanisms defined for PKGs allow reaching the conclusions drawn in the table, which shows the best law that can be applied to each legal case.
- #14 Now, suppose three jurists, Mary, John and Lucy, who have some opinions about these tuples. Our proposal allows them to associate individual subjective opinions to the tuples. Each opinion is represented by the person stating the opinion, their projected probability and their degree of uncertainty. If a user does not express any opinion, we understand that he or she agrees with the prior probability assigned to the fact.
- #15 Then, we can perform the same analysis that we did for the Probabilistic Knowledge Graph, but now on individual basis We are also able to take into account the individual opinions and degrees of uncertainty expressed by the different users. We can see how John thinks that Law 2 should be applied to legal Case 3, whilst Mary thinks that Law 4 should be applied instead, and Lucy thinks it is Law 3.
- #16 More interestingly, we can also merge these individual opinions using the subjective logic fusion operators, such as the Average Belief Function (or ABF). The result of the merge is that law L3 should be applied to legal case 3. Note how, on top of the projected probability, the degree of uncertainty should be considered too, in order to avoid basing decisions on opinions with very high uncertainty levels.
- #17 We have fully implemented our proposal using a graph database, neo4j, and developed the corresponding operations in Java that implement the Subjective Logic operators. These methods can be used from the Cypher language when querying the database and when performing knowledge graph analysis activities.
- #18 For instance, this is the result of the query used to merge the opinions by the three jurists and to compute the results for the three possible laws to apply to legal case 3.
- #19 Finally, we evaluated our proposal, to check 3 main things: First, whether our proposed implementation could deal with large knowledge graphs. Second, if the response times of our queries were acceptable. And third, to measure the overhead of using subjective logic instead of plain probabilities. The results obtained are very promising, as we were able to deal with an existing database of over 2 million nodes and perform queries in the order of milliseconds. Moreover, the overhead introduced by the subjective logic and its operators was only 1.5, which is reasonable for this order of times. Finally, we plan to continue working on this topic along several lines of research. For example, evaluating the usability of our proposal, and investigating different ways of expressing and representing subjective opinions. We also plan to add temporal validity to opinions, and to study how to deal with opinions about correlated facts.
- #20 This is all, thanks for your attention. More information can be found in the paper.