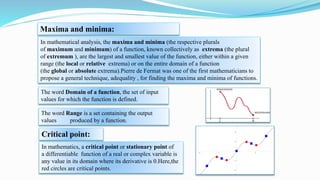
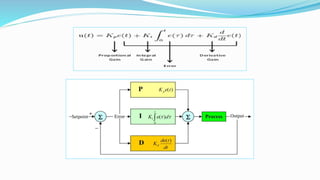
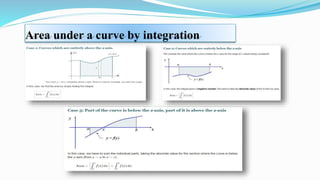
This document is a report submitted by seven students to Sajal Chakroborty on the topic of calculus. It defines calculus and discusses its origins and inventors. It explains that calculus is used in physics, engineering, economics, and other fields. The document then covers topics within calculus including differentiation, integration, maxima and minima, and applications such as modeling tumor growth. It concludes that calculus has many real-world applications and has been crucial to advances in fields like engineering, science, and technology.

1. Submitted To:
Sajal Chakroborty
Prepared By:
S. M. Nahid Hasan
(2016-2-60-024)
Abdullah - Al –Asif
(2016-2-60-066)
MD. Mohaimanul Islam
(2016-2-60-036)
Shammi Akter Vabna
(2016-2-60-020)
Anika barasat
(2016-2-50-016)
Ismot Ara Fatema
(2015-1-53-009)
Saima Akter Urmi
(2016-1-53-025)

2. What is calculus?
• Calculus (from Latin calculus, literally "small pebble used for
counting") is the mathematical study of continuous change, in the
same way that geometry is the study of shape and algebra is the
study of generalizations of arithmetic operations.
• Invention of calculus:
Calculus, known in its early history as infinitesimal calculus, is a
mathematical discipline focused on limits, functions, derivatives,
integrals, and infinite series. Isaac Newton and Gottfried Leibniz
independently discovered calculus in the mid-17th century.

3. Why do we use calculus?
• Among the disciplines that utilize calculus include physics,
engineering, economics, statistics, and medicine. It is used to create
mathematical models in order to arrive into an optimal solution.
 Categories of calculus:

4. Introduction To Differentiation
Differentiate means ‘Find out how fast something is changing in
comparison with something else at any one instant’.
Differentiation finding the instantaneous rate of change , is an essential part
of:
• Mathematics and Physics
• Chemistry
• Biology
• Computer Science
• Engineering
• Navigation and , Astronomy

5. Types of Differentiation:
 Derivatives of Trig Function:
 Derivatives of Hyperbolic Function:
 Implicit Differentiation:
 Logarithmic Function:

6.  It can be used to determine
the rate of change when
figuring out how fast a tumor
is growing/shrinking and is
expressed by an equation :
 V(t) ˭ v . e^( kt )
 Where, v is initial volume of
tumor .
 k is exponential growth
 t is time
 According to the rate, the
chemotherapy other
treatments are prescribed.
How is differentiation
related to tumor
growth?
How does this work?
Graph is computed which measures
therapeutic doses.
Second derivative shows how the
tumor will react to the treatment and
when it should be given.
Computer models are made in order
to arrive to an optimal solution.

7. Maxima and minima:
In mathematical analysis, the maxima and minima (the respective plurals
of maximum and minimum) of a function, known collectively as extrema (the plural
of extremum ), are the largest and smallest value of the function, either within a given
range (the local or relative extrema) or on the entire domain of a function
(the global or absolute extrema).Pierre de Fermat was one of the first mathematicians to
propose a general technique, adequality , for finding the maxima and minima of functions.
The word Domain of a function, the set of input
values for which the function is defined.
The word Range is a set containing the output
values produced by a function.
Critical point:
In mathematics, a critical point or stationary point of
a differentiable function of a real or complex variable is
any value in its domain where its derivative is 0.Here,the
red circles are critical points.

8. What is integration?
Integration is a way of adding slices to find the whole.
Two types of integration:

9. It is the constant of Integration .It is there because of all the functions whose
derivative is 2x.

10. What is controller?

12. Area under a curve by integration

13. Area Between Two Curves Using integration
Alternative Way to Find The
Formula

14. Conclusion of Calculus
Overall the conclusion is calculus is used in various fields like in various
engineering fields, real world application, solving various equations in math.
Even classical mechanics would not have found a place if Leibnitz and
Newton had not invented calculus.
The differentiation and integration of calculus have many real world
application from sports to engineering to astronomy to math and space travel.
space travel would not have been made possible to this extent

15.  Equation based alias calculus for a model programming language with dynamic
memory and decidable arithmetic was developed.
 The calculus mainly used to control flow insensitive safe alias of more programs but
for practical applications of language must be much more realistic
 We were able to obtain an expression for the probability tail of the queuing delay by
using result from the spectral graph theory.
 Business and politicians often conduct surveys with the help of calculus.
As a whole the world without calculus would be like a world without any
advancements in Technology.

16. THANK YOU