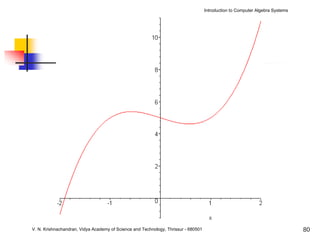
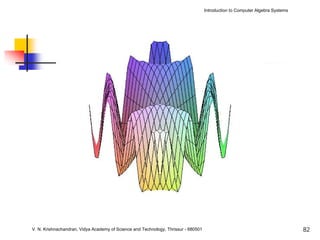
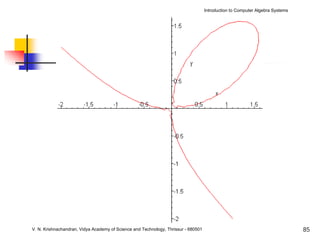
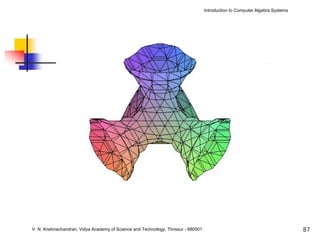
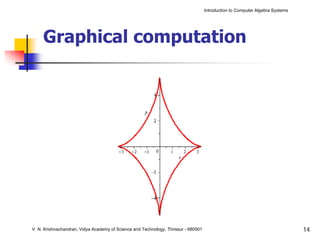
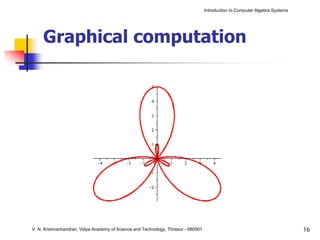
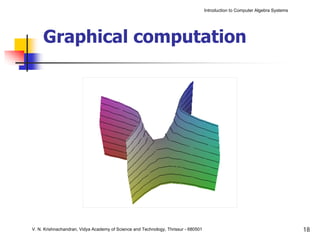
The document is an introduction to computer algebra systems (CAS), detailing their capabilities in numerical, symbolic, and graphical computations, with practical examples using the software Maple. It covers various operations and syntax for algebra, calculus, and solving differential equations within Maple, as well as the application of packages for different mathematical areas. Additionally, it includes multiple examples to demonstrate the functionalities of CAS in solving complex mathematical problems.

1. Computer Algebra Systems
Dr. V. N. Krishnachandran
Department of Computer Applications
Vidya Academy of Science and Technology
Thrissur – 680 501
1

2. Introduction to Computer Algebra Systems
Outline
Introduction
Numerical computations
Symbolic computations
Some popular CAS’s : Maple, Matlab, …
Maple in action
Maple syntax
Algebra with Maple
Calculus with Maple
Differential equations with Maple
Maple packages
LinearAlgebra package
inttrans package
Graphics with Maple
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 2

3. Introduction to Computer Algebra Systems
Introduction
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 3

4. Introduction to Computer Algebra Systems
Computer Algebra Systems
A CAS is a software package having
capabilities for
• numerical computations
• symbolic computations
• graphical computations
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 4

5. Introduction to Computer Algebra Systems
Introduction
Numerical computations
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 5

6. Introduction to Computer Algebra Systems
Numerical computation
Example 1
l
Let T = 2π
g
Find T when g = 981, π = 3.14, l = 51.5 .
Use logarithm tables or an electronic
calculator to calculate this expression
and get T = 1.439 .
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501

7. Introduction to Computer Algebra Systems
Numerical computation
Example 2
Evaluate the following integral using
trapezoidal rule:
1 x 2
−
∫
0
e 2
dx
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 7

8. Introduction to Computer Algebra Systems
Introduction
Symbolic computations
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 8

9. Introduction to Computer Algebra Systems
Symbolic computation
Example 3
Solve the quadratic equation:
( a − b ) x + (b − c ) x + (c − a ) = 0
2
Solution :
c−a
x = 1,
a−b
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501

10. Introduction to Computer Algebra Systems
Symbolic computation
Example 4
Obtain the general solution of the
differential equation:
2
d y dy
2
+ p = ax + b
dx dx
(See next slide for solution)
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 10

11. Introduction to Computer Algebra Systems
Symbolic computation
Example 4 : Solution
Complementary Function = C1 + C2 e − px
1 ⎛ a x 2 + ⎛b − a ⎞x ⎞
Particular Integral = ⎜ ⎜ ⎟ ⎟
p⎝2 ⎝ p⎠ ⎠
y = C. F. + P.I.
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501

12. Introduction to Computer Algebra Systems
Introduction
Graphical computations
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 12

13. Introduction to Computer Algebra Systems
Graphical computation
Example 5
Draw the curve:
(ax ) + (by ) = a − b
2/3 2/3
( 2
)
2 1/ 3
for a = 5 , b = 3
(See next slide for solution)
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 13

14. Introduction to Computer Algebra Systems
Graphical computation
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 14

15. Introduction to Computer Algebra Systems
Graphical computation
Example 6
Draw the curve (polar coordinates):
r = 2 − 3 sin ( 3θ )
(See next slide for solution)
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 15

16. Introduction to Computer Algebra Systems
Graphical computation
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 16

17. Introduction to Computer Algebra Systems
Graphical computation
Example 7
Plot the surface:
x − y = z
2 2
(See next slide for solution)
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 17

18. Introduction to Computer Algebra Systems
Graphical computation
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 18

19. Introduction to Computer Algebra Systems
Introduction
Some popular CAS’s
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 19

20. Introduction to Computer Algebra Systems
Some popular CAS’s
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 20

21. Introduction to Computer Algebra Systems
Some popular CAS’s
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 21

22. Introduction to Computer Algebra Systems
Some popular CAS’s
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 22

23. Introduction to Computer Algebra Systems
Some popular CAS’s
Symbolic Math Toolbox in
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 23

24. Introduction to Computer Algebra Systems
Maple in action
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 24

25. Introduction to Computer Algebra Systems
Maple in action
Maple syntax
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 25

26. Introduction to Computer Algebra Systems
Maple syntax
Operation Symbol Example
Addition + a+b
Subtraction - a-b
Multiplication * a*b
Division / a/b
Exponentiation ^ (**) a^b(a**b)
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 26

27. Introduction to Computer Algebra Systems
Maple syntax
Math Maple Math Maple
sin x sin(x) sin -1 x arcsin(x)
cos x cos(x) cos -1 x arccos(x)
tan x tan(x) tan -1 x arctan(x)
sec x sec(x) sec -1 x arcsec(x)
cosec x csc(x) cosec -1 x arccsc(x)
cot x cot(x) cot -1 x arccot(x)
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 27

28. Introduction to Computer Algebra Systems
Maple syntax
Math Maple
log x log(x)
|x | abs(x)
e^x exp(x)
√x sqrt(x)
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 28

29. Introduction to Computer Algebra Systems
Maple syntax
Example 8
Mathematical expression
−1 ⎛ x ⎞
e ax
cos (bx + c ) + sin
6
1 + log ⎜ 2⎟
⎝x +a ⎠
Maple expression:
exp(a*x)*(cos(b*x+c))^6 + arcsin(
sqrt(1 + log(x/(x+a^2)) ) )
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 29

30. Introduction to Computer Algebra Systems
Maple in action
Algebra with Maple
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 30

31. Introduction to Computer Algebra Systems
Algebra
Example 9
Expand the following and assign
the expression to F:
(x − 2 x y ) 2 3
Maple input
> F:=expand((x-2*x^2*y)^3);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 31

32. Introduction to Computer Algebra Systems
Algebra
Example 9 (continued)
Maple output:
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 32

33. Introduction to Computer Algebra Systems
Algebra
Example 10
To solve the quadratic equation
( a − b ) x + (b − c ) x + ( c − a ) = 0
2
Maple input
> solve( (a-b)*x^2+(b-c)*x+(c-a)=0,x);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 33

34. Introduction to Computer Algebra Systems
Algebra
Example 10 (continued)
Maple output:
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 34

35. Introduction to Computer Algebra Systems
Algebra
Example 11
Solve the cubic equation
2 x +3 x −x +5 =0
3 2
Maple input
> solve(2*x^3+3*x^2-x+5=0,x);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 35

36. Introduction to Computer Algebra Systems
Algebra
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 36

37. Introduction to Computer Algebra Systems
Algebra
Example 12
To find the solutions as floating
point numbers:
Maple input
> evalf(%);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 37

38. Introduction to Computer Algebra Systems
Algebra
Example 12 (continued)
Maple output:
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 38

39. Introduction to Computer Algebra Systems
Maple in action
Calculus with Maple
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 39

40. Introduction to Computer Algebra Systems
Differentiation
General format to evaluate derivatives:
To find
∂
f( x , y , z )
∂y
Maple input:
> diff( f(x,y,z) , y );
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 40

41. Introduction to Computer Algebra Systems
Differentiation
Let us consider the function:
f( x, y, z ) = x e 2 ( −z ) ⎛x⎞
+ ( 2 y − x ) arctan ⎜ ⎟
3
⎜z⎟
⎝ ⎠
Maple input
> f := x^2 * exp(-z) + (2*y^3 - x) *
arctan(x/z);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 41

42. Introduction to Computer Algebra Systems
Differentiation
Example 13
To obtain the derivative of f
with respect to x
Maple input
> diff(f,x);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 42

43. Introduction to Computer Algebra Systems
Differentiation
Example 13 (continued)
Maple output:
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 43

44. Introduction to Computer Algebra Systems
Differentiation
Example 14
To find
∂2
f( x , y , z )
∂y ∂z
Maple input
> diff(f, y, z) ;
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 44

45. Introduction to Computer Algebra Systems
Differentiation
Example 14 (continued)
Maple output:
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 45

46. Introduction to Computer Algebra Systems
Differentiation
Example 15
To obtain the taylor series
x
(x + 1 ) (x − 2 )
Maple input
> taylor( x/((x+1)*(x-2)), x=1, 4);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 46

47. Introduction to Computer Algebra Systems
Differentiation
Example 15 (continued)
Maple output:
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 47

48. Introduction to Computer Algebra Systems
Integration
The general format for evaluating
indefinite integrals: To find
∫ f ( x) dx
Maple input
> int(f(x),x);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 48

49. Introduction to Computer Algebra Systems
Integration
Example 16
A simple example:
∫ (x − sin( x) dx )
2
Maple input
> int(x^2 - sin(x), x);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 49

50. Introduction to Computer Algebra Systems
Integration
Example 16 (continued)
Maple output:
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 50

51. Introduction to Computer Algebra Systems
Integration
Example 17
A very complicated integral
ax + b
∫ px + qx + r
2
dx
Maple input
> int( (a*x+b)/sqrt(p*x^2+q*x+r) , x );
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 51

52. Introduction to Computer Algebra Systems
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 52

53. Introduction to Computer Algebra Systems
Integration
Example 18
Sometimes Maple may not be able to
obtain an explicit expression for an
integral.
∫
x
x dx
Maple input
> int(x^x,x);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 53

54. Introduction to Computer Algebra Systems
Integration
Example 18 (continued)
Maple output:
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 54

55. Introduction to Computer Algebra Systems
Integration
The general format for evaluating
definite integrals: To find
b
∫ f ( x)dx
a
Maple input:
> int ( f(x) , x=a..b );
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 55

56. Introduction to Computer Algebra Systems
Integration
Example 19
Evaluate:
1
x
∫ 1+ x2
0
dx
Maple input
> int(x/(1+x^2), x = 0 .. 1);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 56

57. Introduction to Computer Algebra Systems
Integration
Example 20
Limits can contain π (Pi) and ∞ (infinity)
π /2
∫ x sin( nx ) dx
π
− /2
Maple input
> int(x*sin(n*x), x=-Pi/2 .. Pi/2);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501

58. Introduction to Computer Algebra Systems
Integration
Example 20 (continued)
Maple output
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 58

59. Introduction to Computer Algebra Systems
Maple in action
Differential equations
with Maple
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 59

60. Introduction to Computer Algebra Systems
Differential equations
Example 21
First order equations
dy
x +y=x
dx
Maple input
> dsolve( x*diff(y(x), x) + y(x) = x );
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501
60

61. Introduction to Computer Algebra Systems
Differential equations
Example 21 (continued)
Maple output
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 61

62. Introduction to Computer Algebra Systems
Differential equations
Example 22
Second order equations
2
d y
2
+a y = x
2
dx
Maple input
> dsolve( diff(y(x),x,x)+a^2*y(x)=x);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 62

63. Introduction to Computer Algebra Systems
Differential equations
Example 22 (continued)
Maple output
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 63

64. Introduction to Computer Algebra Systems
Maple in action
Maple packages
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 64

65. Introduction to Computer Algebra Systems
Packages
Some packages
combinat combinatorial functions
inttrans integral transforms
LinearAlgebra Linear algebra
networks graph networks
numtheory number theory
plots displaying graphs
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 65

66. Introduction to Computer Algebra Systems
Maple in action
LinearAlgebra package
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 66

67. Introduction to Computer Algebra Systems
LinearAlgebra package
This is a collection of functions
for symbolic computations
involving vectors and matrices.
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 67

68. Introduction to Computer Algebra Systems
LinearAlgebra package
Load LinearAlgebra package
> with(LinearAlgebra);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 68

69. Introduction to Computer Algebra Systems
LinearAlgebra package
To define the matrix
⎡ 1 −3 4⎤
⎢
⎢ 2 ⎥
⎢ 3 4⎥
⎥
⎢
⎢−4 ⎥
⎣ 0 5⎥
⎦
Maple input
>A:=Matrix([[1, -3, 4],[2, 3, 4],[-4, 0, 5]]);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 69

70. Introduction to Computer Algebra Systems
LinearAlgebra package
Example 23
To find the inverse of A
Maple input
> MatrixInverse(A);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 70

71. Introduction to Computer Algebra Systems
LinearAlgebra package
Example 24
To find the characteristic polynomial
in terms of lambda
Maple input>
CharacteristicPolynomial(A,lambda);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 71

72. Introduction to Computer Algebra Systems
LinearAlgebra package
Example 25
To find the eigen values of A
Maple input
> Eigenvalues(A);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 72

73. Introduction to Computer Algebra Systems
Maple in action
inttrans package
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 73

74. Introduction to Computer Algebra Systems
inttrans package
The inttrans package is a collection of
functions designed to compute integral
transforms like Laplace transforms and
Fourier transforms.
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 74

75. Introduction to Computer Algebra Systems
inttrans package
To load inttrans packge
> with(inttrans);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 75

76. Introduction to Computer Algebra Systems
inttrans package
Example 26
To find the Laplace transform of
2 −4 t
t sin( 3 t ) e
Maple input
> laplace(t^2*sin(3*t)*exp(-4*t), t, s);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 76

77. Introduction to Computer Algebra Systems
inttrans package
Example 27
To find the inverse Laplace transform of
s
(s 2
+ s +1 ) 2
Maple input
> invlaplace(s/((s^2+s+1)^2), s, t);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 77

78. Introduction to Computer Algebra Systems
Maple in action
Graphics with Maple
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 78

79. Introduction to Computer Algebra Systems
Graphics
Example 28
To plot the graph of the function
x −x+5
3
Maple input
> plot( x**3 – x + 5 , x = -2..2 );
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 79

80. Introduction to Computer Algebra Systems
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 80

81. Introduction to Computer Algebra Systems
Graphics
Example 29
To plot the surface given by the function
f ( x , y ) = sin( xy )
Maple input
> plot3d(sin(x*y), x=-Pi..Pi, y=-Pi..Pi);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 81

82. Introduction to Computer Algebra Systems
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 82

83. Introduction to Computer Algebra Systems
Graphics:plots package
To use the plots package
> with(plots);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 83

84. Introduction to Computer Algebra Systems
Graphics:plots package
Example 30
To plot the curve given by the equation
x + y = 3 xy
3 3
Maple input
> implicitplot(x^3 + y^3 = 3*x*y,
x = -2..2, y = -2..2);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 84

85. Introduction to Computer Algebra Systems
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 85

86. Introduction to Computer Algebra Systems
Graphics:plots package
Example 31
To plot the surface given by the equation
x + y + z + 1 = ( x + y + z + 1)
3 3 3 3
Maple input
> implicitplot3d( x^3 + y^3 + z^3 +1
= (x+y+z+1)^3, x=-2..2, y=-2..2, z=-
2..2);
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 86

87. Introduction to Computer Algebra Systems
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 87

88. Introduction to Computer Algebra Systems
THANK YOU …
V. N. Krishnachandran, Vidya Academy of Science and Technology, Thrissur - 680501 88