This document provides an overview of three-dimensional displays, from physiological depth cues to electronic holograms. It discusses depth cues our eyes use to perceive depth, including psychological cues like occlusion and physiological cues like binocular disparity. Examples of 3D displays that provide some depth cues, like lenticular sheets, are described. The document also covers holograms, including how they can provide all depth cues by reconstructing the original wavefront. It discusses challenges like the large amount of information in holograms and methods to reduce it, like rainbow and multiplex holograms. Computer generated and electronic holograms using dynamic modulators are also summarized.

1. Brief survey on Three-Dimensional Displays:
from Our Eyes to Electronic Hologram*
Taufiq Widjanarko
*Presented at ECPE 4144 Optical Information Processing, Project Term Paper, Virginia Tech, Fall 2001. Last modified 19 March 2013

2. Outline
• Depth Cues
• Examples of Three-Dimensional Displays
• Wavefront Reconstruction
• Examples of Hologram
– Off-axis Hologram
– Reflection Hologram
• Information Content in Hologram
• Method to reduce profuse information content
– Rainbow Hologram
– Multiplex Hologram
• Computer Generated Hologram
• Electronic Hologram
– Optical Scanning Holography
– Holographic Video

3. Depth Cues
• Visual depth sense is often taken for granted until we
encounter the problem that can be solved if depth cues
are present
• Depth Cues can be grouped into two major categories [1]:
1.Psychological (Pictorial) Depth Cues: depth cues
influenced by the mental and prior knowledge of the
observer
2.Physiological Depth Cues: depth cues related to the
physiology of our eyes

4. Psychological Depth Cues
• Retinal Image Size:
different image size
appearance on
retina
• Aerial Perspective
• Linear Perspective
Figure taken from Ref.[1]

5. Psychological Depth Cues(Cont’d)
• Occlusion
• Shading
Figures taken from Ref.[1]

6. Psychological Depth Cues(Cont’d)
• Texture Gradient
Figure taken from Ref.[1]

7. Physiological Depth Cues
• Accommodation:
Change of eye
muscular tension to
adjust the focal length
• Convergence: eyes
ability to fixate a point
on the object
dα PO
= 2
da a
P0 = two pupil separation
a = object distance
Figure taken from Ref.[1]

8. Physiological Depth Cues (Cont’d)
• Binocular Disparity/Stereospsis
Dαθ
2
∆D ≅
PO
Figure taken from Ref.[1]
• Motion Parallax: different angular velocity of
object at different depths the observer

9. Example of Three-Dimensional Displays
• Integral Photography: using lenslet array to sample
the object
Figures taken from Refs.[1,8]

10. Example of Three-Dimensional Displays(Cont’d)
• Lenticular Sheet
x Figures taken from Ref.[1,2]
θ=
f

11. Example of Three-Dimensional Displays(Cont’d)
• Parallax Barrier
Figures taken from Refs.[1,2]
viewing distance = .25 m, p < .08 mm → for slit width
1/10 of pitch = 8 µm or only 15 x λvisible

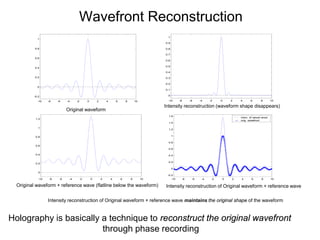
12. Three mechanisms of eyes in responding
the incoming wavefront [12,26]
1. Modifies and the focus the wavefront to retina
→Accommodation
2. Sample the wavefront from two slightly different positions and
interpreted as different position in two visual field
→Convergence and Stereopsis
3. Moving observer samples the wavefront from different
positions and object’s position in visual field changes as the
result of observer’s motion
→Motion Parallax
To present all 4 physiological depth cues
 Provide or reconstruct the original object’s wavefront

13. Wavefront Reconstruction
1
1
0.9
0.8 0.8
0.7
0.6
0.6
0.5
0.4
0.4
0.2 0.3
0.2
0
0.1
-0.2 0
-10 -8 -6 -4 -2 0 2 4 6 8 10 -10 -8 -6 -4 -2 0 2 4 6 8 10
Intensity reconstruction (waveform shape disappears)
Original waveform
1.6
inten. of raised ampl.
1.2
orig. wavefront
1.4
1
1.2
0.8 1
0.8
0.6
0.6
0.4 0.4
0.2
0.2
0
0
-0.2
-10 -8 -6 -4 -2 0 2 4 6 8 10 -10 -8 -6 -4 -2 0 2 4 6 8 10
Original waveform + reference wave (flatline below the waveform) Intensity reconstruction of Original waveform + reference wave
Intensity reconstruction of Original waveform + reference wave maintains the original shape of the waveform
Holography is basically a technique to reconstruct the original wavefront
through phase recording

14. Examples of Hologram
• Transmission Hologram
• Reflection hologram
Figures taken from Refs.[6,8]

15. Information Content in a Hologram [23,28]
• Grating equation λf h = sin θ
– fh highest frequency comp. of object
• Required sampling freq sin θ
fs = 2 fh = 2
– fs = sampling frequency λ
• N= Number of sampling (in horizontal direction) 2d sin θ
N = df s =
– d = width of hologram in horizontal direction λ
• Nt= Total number of sample in both horizontal and vertical direction
– w=width of hologram in vertical direction 4dw sin θ
Nt =
λ2
• 100 x 100 mm2, 30° view angle →2.5x1010 samples/frame
• Real time hologram of 60 frames per second requires
→1.2x1012 bit/sec (fastest conventional display rate 2 Gbits/s) [23,28]

16. Holographic Information Reduction Method
• Rainbow Hologram
horizontal slit is to remove vertical parallax
→reduce information content Figures taken from Ref.[8]

17. Holographic Information Reduction Method (Cont’d)
• Multiplex Hologram (Holographic Stereogram)
– Proposed by De Bitteto
Figures taken from Ref.[8]

18. Holographic Stereogram (Cont’d)
• Cross Hologram
Figures taken from Ref.[3,4,6]
→both hologram exhibit no vertical parallax

19. Computer Generated Hologram
• Binary Detour Phase Method: to create Fourier
Hologram
– Final image must be in the form of
N X −1 N Y −1 2π
( up∆x + vq∆y )
∑ ∑a
j
jφ pq λf
U f ( u, v ) = pq e e
p=0 q =0
– Cell aperture transmittance
 x − x0   y − y0 
t A ( x , y ) = rect   
 w X   wY 
– Inclined plane wave illumination
Figures taken from Ref.[4]
U p = e − j 2παx

20. Computer Generated Hologram (Cont’d)
• After illumination
− j 2 παx  x − x0   y − y0 
U t ( x, y) = e rect 
 wx  
 w  
y 
• At Fourier Plane
2π
w w  w ( u + λfα )   w v  j [ ( u + fλα ) x0 + vy0 ]
U f (u, v ) = X Y sin c  X  sin c  Y e λf
λf  λf   λf 
• After some assumptions, simplifications and
setting the offset ( x ) = p∆x & ( y ) = q∆y 0 pq 0 pq
N X −1 N Y −1 2π
( up∆x + vq∆y )
∑ ∑ (w
j
U f ( u, v ) = X ) pq ( wY ) pq e j 2πp e λf
p=0 q =0

21. Computer Generated Hologram (Cont’d)
• Shifting the aperture center ( x ) 0 pq = p∆x + (δx ) pq
( δx ) pq 2π
N X −1 N Y −1
j 2π (
up∆x + u ( δx ) pq + vq∆y )
∑ ∑ ( wX ) pq ( wY ) pq e
j
λf
U f ( u, v ) = ∆x
e
p=0 q =0
• With several assumption, the above expression
can be simplified as δ π
N X −1 N Y −1 ( ) ( x ) pq 2
up∆x + vq∆y
π
U ( u, v ) = ∑ ∑ ( w ) ( w ) e
j2 j
λ ∆x f
f e
X pq Y pq
p=0 q =0
• Compared with the desired form
π
N X −1 N Y −1 2
( ) up∆x + vq∆y
U ( u, v ) = ∑ ∑ a e e
j
φ λ j pq f
f pq
p=0 q =0
• Phase and amplitude relation to the cell aperture
2π (δx ) pq
φ pq = − & ( wY ) pq ∝ a pq
∆x

22. Computer Generated Hologram (Cont’d)
Figures taken from Ref.[4]

23. Electronic Holography
• Using dynamic electronically-controlled optical modulator
1. Optical Scanning Holography: scanning TDFZP to obtain the
scanned holographic pattern of the object
Application in fluorescence microscopy: for image region 2 x 2
mm2, the system can reveal lateral and axial resolution of 7.7
and 200 µm, respectively
Figures taken from Ref.[5,16]

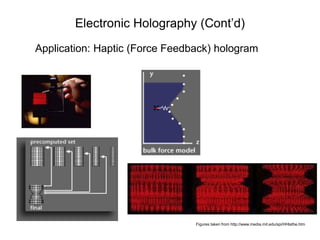
24. Electronic Holography (Cont’d)
– Holographic video (Media Lab MIT)
• inspired by binary detour phase, holographic
stereogram and rainbow hologram
• using AOM to diffract light into desired point in
volume space
• fringe calculation is similar to computer
graphics
Figures taken from Ref.[29]

25. Electronic Holography (Cont’d)
• A single hologram lines is decomposed into pre-
computed ‘basis fringe’ → orthogonal basis function
decomposition
• First generation: full color 25x25x25 mm3, 15°viewing
angle, 20 frames/second
• Second generation: 80x140x150 mm3, 2.5
frames/second
Figure taken from http://www.media.mit.edu/spi/HVmark2.htm

26. Electronic Holography (Cont’d)
Application: Haptic (Force Feedback) hologram
Figures taken from http://www.media.mit.edu/spi/HHlathe.htm

27. Electronic Holography (Cont’d)
– Potential application: telesurgery,
telemanufacturing, etc
Figure taken from http://www.media.mit.edu/spi/HHlathe.htm

28. Conclusion
• Depth Cues:
– Psychological or Pictorial cues (based on mental and prior
knowledge of observer): retinal image size, aerial and linear
perspective, occlusion, shading and texture gradient
– Physiological depth cues: accommodation, binocular disparity,
convergence and motion parallax
– 3-D displays prior to hologram can only provide the last three
physiological cues
– Hologram can naturally provide all physiological & psychological
depth cues due to its nature to reconstruct object wavefront
• Off axis hologram can solve initial Gabor’s hologram problem
• Information content in a hologram is tremendously profuse→ 100 x 100
mm2, 30° view angle requires 2.5x1010 samples/frame
• Some proposed method to reduce information content are rainbow
hologram and multiplex hologram (holographic stereogram)
→sacrificing vertical parallax to reduce information content

29. Conclusion (Cont’d)
• The earliest Computer Generated Hologram method: the Binary
Detour Phase Hologram uses aperture within a cell to encode
the amplitude (from aperture area) and phase (from center of
aperture shift). Plotted pattern quality is determined by
resolution of the writing device
• Recent Electronic Holograms use dynamic optical modulator,
such as AOM, LCD as a light diffracting component.AOM are
used in optical scanning holography and holographic video

30. Full paper available at
http://www.academia.edu/1158381/Brief_Survey_on_Three-Dimensional_Displays_2001_

31. References
1. T. Okoshi, “Three-Dimensional Imaging Techniques”, Academic Press, New York (1976)
2. M. McKenna & D. Zeltzer, Presence (1)4, 421 (1992)
3. P. Hariharan, “Optical Holography: Principles, Techniques and Applications”, 2nd ed, Cambridge University Press, Cambridge (1996)
4. J. W. Goodman, “Introduction to Fourier Optics”, McGraw-Hill, NY (1996)
5. T-C. Poon and P. P. Banerjee, “Contemporary Optical Information Processing With Matlab®”, Elsevier, Oxford (2001)
6. F. Unterseher, J. Hansen and R. Schlesinger, “Holography Handbook: Making Holograms the Easy Way”, Ross Book, Berkeley, CA (1982)
7. E. N. Leith, “White-Light Holograms”, Sci. Am.
8. G. Saxby, “Practical Holography”, Prentice-Hall International, Hertfordshire (1988)
9. S. A. Benton, “Holography: The Second Decade”, Opt. News, Optical Society of America, pp. 16-21 (Summer 1977)
10. L. Huff & R. L. Fusek, Opt. Eng. (9)5,691 (1980)
11. S.A. Benton, Proc. SPIE vol 532, pp 8-13 (1985)
12. M. W. Halle, Proc. SPIE vol 2176, 73(1994)
13. A. W. Lohmann and D. P. Paris, App. Opt.(6), 1739 (1967)
14. W. J. Dallas, “Computer Generated Hologram”, in The Computer in Optical Research, Topics in Applied Physics, B. R. Frieden ed., Springer-
Verlag, Berlin, pp 291-366 (1980)
15. T-C. Poon and A. Korpel, Opt. Lett.(10) 317 (1979)
16. T-C. Poon, M. H. Wu, K. Shinoda and Y. Suzuki, Proc. IEEE vol. 84, 5 (1996)
17. T-C. Poon, JOSA.A (2)4,521 (1985)
18. M. Lucente, P. St-Hillaire, S. A. Benton, D. L. Arias and J. A. Watlington, Proc. SPIE vol 1732, 377(1992)
19. P. St-Hillaire, S. A. Benton, M. Lucente, J. D. Sutter and W. J. Plesniak, Proc. SPIE vol 1914, 188 (1993)
20. R. Pappu and W. J. Plesniak, “Haptic Interaction with Holographic Video Images”, Practical Holography XII, Proc. SPIE (1998)
21. S. A. Benton, private communication (2001)
22. M. W. Halle, Proc SPIE 2176, 75 (1994)
23. P. St-Hillaire, “Scalable Optical Architectures for Electronic Holography”, Dissertation, Massachusetts Institute of Technology (1994).
24. H. J. Caulfield and S. Lu, “Application of Holography”, Wiley-Interscience, NY (1970)
25. M. W. Halle, “The Generalized Holographic Stereogram”, Master Thesis, Massachusetts Institute of Technology (1991)
26. M. W. Halle, “Multiple Viewpoint Rendering for Three-Dimensional Displays”, Dissertation, Massachusetts Institute of Technology (1997)
27. B.W. Schilling, T-C. Poon, G. Indebetouw, B. Storrie, K. Shinoda, Y. Suzuki and M. H. Wu, Optics Letters (22)19 (1997)
28. M. Lucente, “ Diffraction-Specific Fringe Calculation for Electro-Holography”. Dissertation, Massachusetts Institute of Technology (1994)
29. R. Haralick, L.Shapiro,”Computer and Robot Vision”,Addison Wesley (1992)