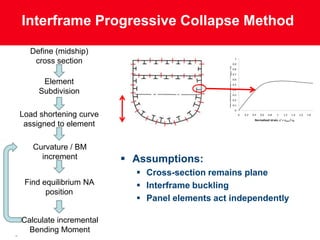
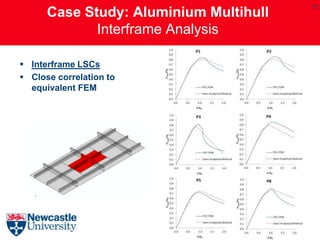
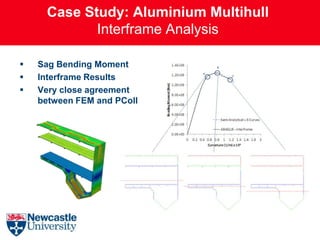
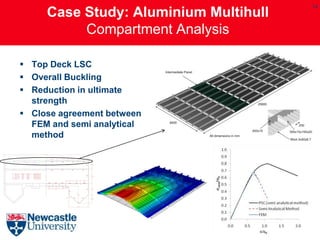
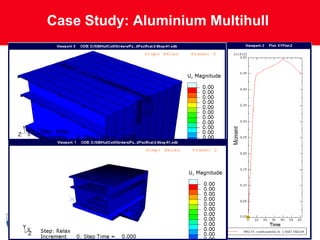
This document describes the development and extension of hull girder progressive collapse analysis methods for lightweight naval vessels. It presents the Smith Progressive Collapse Method and introduces the Extended Progressive Collapse Method, which adapts the approach to consider compartment-level elements rather than assuming independent interframe behavior. A case study analysis of an aluminum multihull vessel's longitudinal bending capacity is performed using the extended method and compared to nonlinear finite element analysis results, showing close agreement. The extended method and its ProColl implementation provide a simplified but accurate means of assessing the ultimate strength and collapse behavior of lightweight hull structures.

1. COMPARTMENT LEVEL PROGRESSIVE COLLAPSE
ANALYSIS OF A LIGHTWEIGHT HULL GIRDER
Simon Benson, Jonathan Downes and Robert S. Dow
School of Marine Science and Technology

2. 2
Contents
 Motivation
 The Smith Progressive Collapse Method
 The Extended Progressive Collapse Method
 Case Study – Aluminium Multihull
 Conclusions

3. 3
Motivation
 Office of Naval Research (ONR) project:
“Structural Performance of Lightweight Naval Vessels”
 Development and extension of hull girder progressive
collapse analysis methodologies:
 Ultimate Strength Analysis
 Limit State Design
 Optimisation
 Reliability
 Damage Strength
 Recoverability
 Evaluation of longitudinal bending capacity of the hull girder
 Solution methods:
 Simplified Progressive Collapse Analysis
 Nonlinear Finite Element Analysis

4. Motivation
 Established hull girder progressive collapse methods have
been developed primarily for STEEL ships.
 How do we adapt these approaches to lightweight ships?
 Two general approaches:
 Simplified analytical methods (e.g. progressive collapse):
 Fast and efficient
 Simplifying assumptions
 Implicit characterisation of material and geometric imperfections
 Nonlinear finite element methods (FEM):
 Computationally expensive
 Requires explicit characterisation of all material and geometric properties in
the FE model
 Which methods are suitable for reliability analysis?

5. Interframe Progressive Collapse Method
5083-H116 Plate Load Shortening Curves
Define (midship) HAZ Ratio (HR) = 8
cross section 1
0.9
Normalised Stress, s' = save / s0
0.8
0.7
Element 0.6
0.5
b=2
Subdivision 0.4
0.3
0.2
0.1
0
Load shortening curve 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
Normalised strain, e' = e ave / e 0
assigned to element
Curvature / BM
increment  Assumptions:
 Cross-section remains plane
1.50
Bending Moment, Mx (N.mm) x 10-10
1.00
Find equilibrium NA  Interframe buckling 0.50
position hog
 Panel elements act independently 0.00
sag
-0.50 Progressive Collapse - 150mm hard corners
Abaqus 5bay model (50mm element size)
-1.00
Calculate incremental Abaqus 5bay model (25mm element size)
-1.50
Bending Moment -4.00 -3.00 -2.00 -1.00 0.00 1.00 2.00 3.00 4.00
Curvature, C (1/mm) x 106

6. Extended Progressive Collapse Method
Define (midship)
cross section
 Extends the approach used to define the
Element element behaviour
Subdivision  Revised Assumptions:
 Cross section remains plane (as before)
Load shortening curve  Compartment level elements
assigned to element  Elements do not act independently
 Interframe and overall buckling properties
Curvature / BM combined
increment
Find equilibrium NA
position
Calculate incremental
Bending Moment

7. 7
Extended Progressive Collapse Method
Element Definition
 Standard approach:
 Plate-stiffener combination elements
 Hard corners
 Each element assigned a load
shortening curve (LSC)
 Element does not have to
correspond directly to LSC
 Refine for accuracy in calculations
 LSC can represent global elements
 LSC can be calculated for:
 Components (plates, stiffeners)
 Plate-stiffener combinations
 Orthogonal stiffened panels
 Panel strength calculated by a semi
analytical orthotropic plate method

8. 8
Extended Progressive Collapse Method
Panel Load Shortening Curves
 Derived using a semi analytical method
 Increments of end strain/displacement
 At each increment:
1. Evaluate component (plate and stiffener) resistance
2. Calculate combined resistance
3. Evaluate beam column (interframe) strength and compare
4. Evaluate panel (overall) strength and compare
5. Derive increment of load shortening curve
 Panel strength derived using a large deflection orthotropic
plate method
 Method uses instantaneous component stiffness properties
 Panel LSC can be assigned to small elements

9. 9
Extended Progressive Collapse Method
Implementation - ProColl
 A GUI Interface for the extended
progressive collapse method
 Interframe and compartment
level analyses
 Runs vertical bending or
combinations of vertical and
horizontal (interaction diagram)
 Increments of curvature or
bending moment
 Post processor capabilities
 Generate element load
shortening curves
 Process BM vs. curvature plots
 Graphically display element
stiffness and NA position

10. Case Study: Aluminium Multihull

11. Case Study: Aluminium Multihull

12. 12
Case Study: Aluminium Multihull
Interframe Analysis
 Interframe LSCs
 Close correlation to
equivalent FEM

13. Case Study: Aluminium Multihull
Interframe Analysis
 Sag Bending Moment
 Interframe Results
 Very close agreement
between FEM and PColl

14. 14
Case Study: Aluminium Multihull
Compartment Analysis
 Top Deck LSC
 Overall Buckling
 Reduction in ultimate
strength
 Close agreement between
FEM and semi analytical
method

15. Case Study: Aluminium Multihull
Compartment Analysis
 7 bay results:
 reduction in ultimate strength
 Buckling of top deck prior to
ultimate strength point
 Buckling of second deck at ultimate
strength point
 Close agreement between FEM and
PColl
 Top Deck Load Shortening
Curve:
 Accounts for different longitudinal
stiffener sizes

16. Case Study: Aluminium Multihull
16

17. 17
Conclusions
 We propose an extended progressive collapse methodology
 Utilises a semi analytical method to predict compartment level load
shortening curves
 Case study progressive collapse assessment of an aluminium multihull is
presented:
 Shows significant strength reduction due to compartment level buckling
 Good correlation to FEM results
 Both FEM and simplified methods can produce reasonable and valid
solutions for the compartment level progressive collapse problem

18. Thank you
http://www.ncl.ac.uk/marine/
http://sibenson.wordpress.com