This document discusses affine array accesses in compiler design. It defines an affine access as one where the array index is expressed as an affine expression of loop indexes and constants. Affine accesses can be represented as a matrix-vector calculation that maps the iteration space to data space. Examples are given of affine accesses and how they can be written as tuples representing the mapping between indexes and array elements. Non-affine accesses are also discussed, such as those involving sparse matrices. Exercises are provided to represent given array accesses as affine tuples.

1. OMPILER DESIGN
BY,
ISHWARIYA.R, M.Sc(cs).,
NSCAS,Theni.

2.  The class of affine array access, where each array index is
expressed as affine expressions of loop indexes and symbolic
constants.
 Affine functions provide a succinct mapping from the iteration
space to the data space, making it easy to determine which
iterations map to the same data or same cache line.
 The affine upper and lower bounds of a loop can be
represented as a matrix-vector calculation.
Affine Array Index

3. Affine Array Indexes
1.Affine Accesses
2.Affine and Nonaffine Accesses in Practice
3.Exercises for Section 11.4

4. 1. Affine Accesses
We say that an array access in a loop is affine if,
1. The bounds of the loop are expressed as affine expressions of
the sur-rounding loop variables and symbolic constants,
2. The index for each dimension of the array is also an affine
expression of surrounding loop variables and symbolic constants.

5. Formally, we represent an array access in a loop nest that uses a
vector of index variables i by the four-tuple T = (F,f,B>b); it
maps a vector i within the bounds
Bi + b > 0
To the array element location
Fi + f

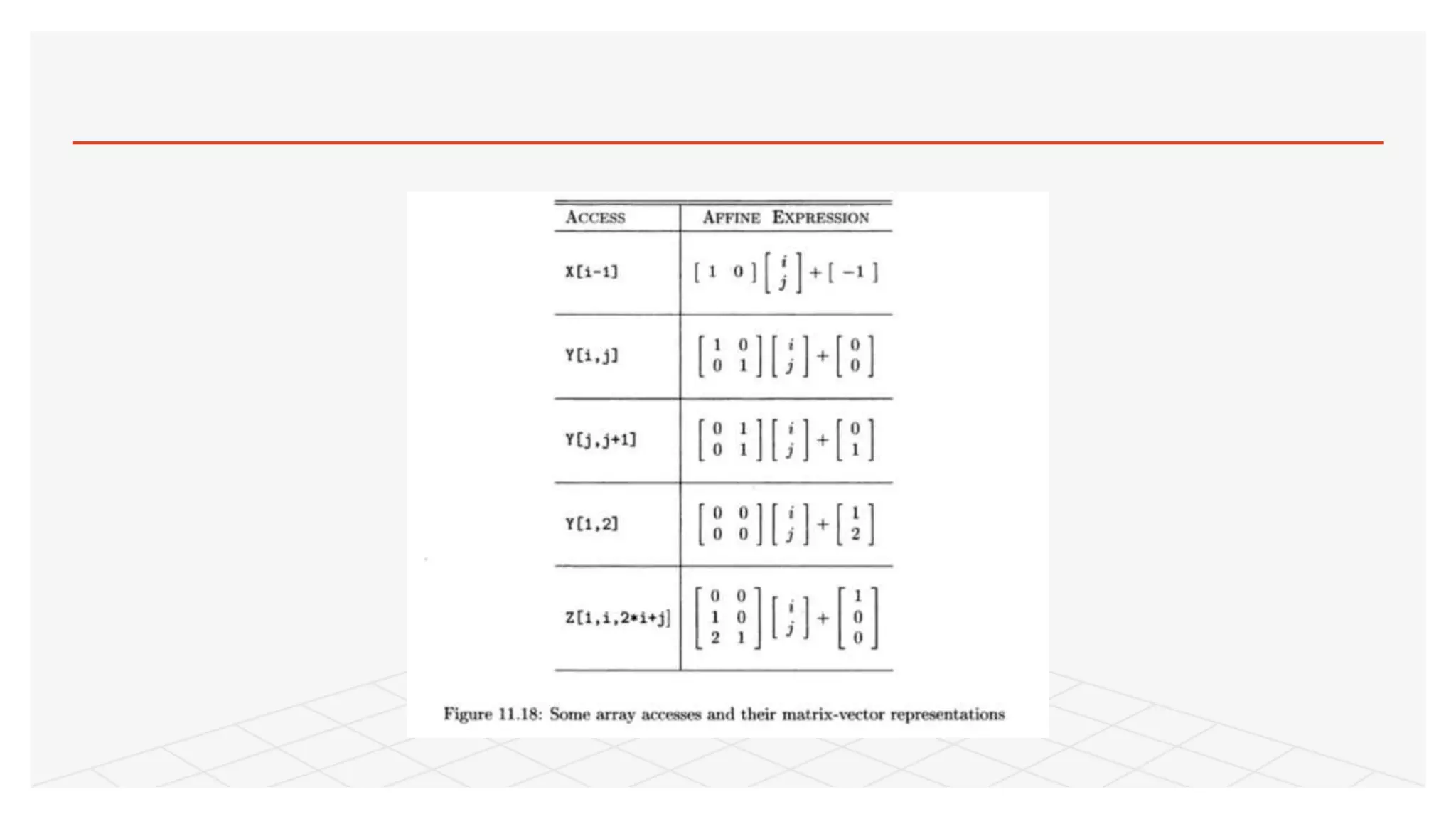
6. The two loop indexes are i and j, and these form the vector i. Also, X, Y,
and Z are arrays with 1, 2, and 3 dimensions, respectively. The first access,
A[i - 1], is represented by a 1 x 2 matrix F and a vector f of length 1. Notice
that when we perform the matrix-vector multiplication and add in the
vector f, we are left with a single function, which is exactly the formula for
the access to the one-dimensional array X. Also notice the third access,
Y[j,j + 1], which, after matrix-vector multiplication and addition, yields a
pair of functions, (J,j + 1). These are the indexes of the two dimensions of
the array access. Finally, let us observe the fourth access K[l,2] . This
access is a constant, and unsurprisingly the matrix F is all 0's. Thus, the
vector of loop indexes, i, does not appear in the access function.
Example 11 . 17:

8. There are certain common data access patterns found in numerical
programs that fail to be affine. Programs involving sparse matrices are one
important example. One popular representation for sparse matrices is to
store only the nonzero elements in a vector, and auxiliary index arrays are
used to mark where a row starts and which columns contain nonzeros.
Indirect array accesses are used in accessing such data. An access of this
type, such as nonaffine access to the array X. If the sparsity is regular, as in
banded matrices having nonzeros only around the diagonal, then dense
arrays can be used to represent the subregions with nonzero elements. In
that case, accesses may be affine.
2. Affine and Nonaffine Accesses in Practice

9. Another common example of nonaffine accesses is linearized arrays. Pro-
grammers sometimes use a linear array to store a logically
multidimensional object. One reason why this is the case is that the
dimensions of the array may not be known at compile time. An access that
would normally look like Z[i,j] would be expressed as Z[i * n + j], which
is a quadratic function. We can convert the linear access into a
multidimensional access if every access can be decomposed into separate
dimensions with the guarantee that none of the components exceeds its
bound. Finally, we note that induction-variable analy-ses can be used to
convert some nonaffine accesses into affine ones, as shown in Example
11.18.

11. Exercise 11.4.1 : For each of the following array accesses,
give the vector f and the matrix F that describe them.
3. Exercises for Section 11.4

12. Thank you..