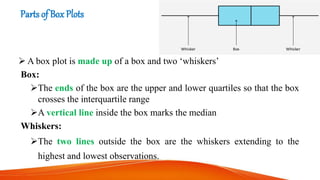
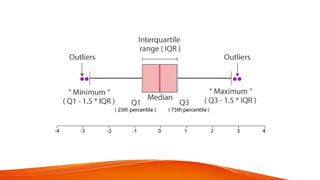
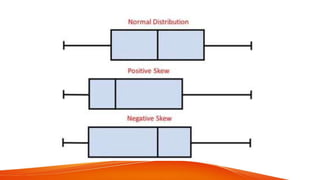
This document provides an introduction to box plots, including their anatomy, parts, and applications. It discusses the five number summary used to construct box plots, which includes the minimum, first quartile, median, third quartile, and maximum. Examples are given to demonstrate how to construct a box plot from a data set by ordering the values, finding the five number summary, and plotting the box and whiskers on a number line. Box plots can show the distribution, outliers, and skew of a data set.

1. Topic:
BOX PLOTs
Presented By: ALI HAIDER
ROLL number : 0003.BS.ZOO.2019
semester: 4th
Group No. 4
department : Zoology

2. Table of content:
Introduction of Box Plot
Parts of Box Plot
Box Plot Anatomy
Other terms used in Box Plot
Applications
Box plot distribution
Steps in making Box Plot
Example

3. Introduction
 Box plots is defined as:
“A Box Plot shows the distribution of a set of
data along a number line, dividing the data into four parts using the
median and quartiles.”
 The term “box plot” refers to an outlier box plot; this plot is also called a
box-and-whisker plot or a Tukey box plot.
 Mathematician John Tukey first introduced the “Box and Whisker Plot”
in 1969 as a visual diagram of the “Five Number Summary” of any given
data set. Box plots can be drawn either vertically or horizontally.

4. Parts of Box Plots
 A box plot is made up of a box and two ‘whiskers’
Box:
The ends of the box are the upper and lower quartiles so that the box
crosses the interquartile range
A vertical line inside the box marks the median
Whiskers:
The two lines outside the box are the whiskers extending to the
highest and lowest observations.

5. Box Plot Anatomy
 A box and whisker plot displays the visual representation of five-
number summary of a data set. A Five Number Summary includes:
i. Minimum Value
ii. First Quartile
iii. Median (Second Quartile)
iv. Third Quartile
v. Maximum Value

6. Minimum: The minimum value in the given dataset
First Quartile (Q1): The first quartile is the median of the lower half
of the data set.
Median: The median is the middle value of the dataset, which divides
the given dataset into two equal parts. The median is considered as the
second quartile.
Third Quartile (Q3): The third quartile is the median of the upper
half of the data.
Maximum: The maximum value in the given dataset.

7. OTHERTERMS IN BOX PLOT
Apart from these five terms, the other terms used in the box plot are:
 Interquartile Range (IQR): The difference between the third quartile
and first quartile is known as the interquartile range.
IQR = Q3-Q1
 Outlier: The data that falls on the far left or right side of the ordered
data is tested to be the outliers. Generally, the outliers fall more than
the specified distance from the first and third quartile.
 Outliers are greater than Q3+(1.5 . IQR) or less than Q1-(1.5 . IQR).

9. APPLICATIONS:
1. A boxplot is a graph that gives you a good indication of how the
values in the data are spread out.
2. Box plots are useful as they show the skewness of a data set.
3. Box plots are useful as they show the dispersion of a data set.
4. Box plots are useful as they show outliers within a data set.

10. Box plot distribution
 Positively Skewed: If the distance from the median to the maximum is
greater than the distance from the median to the minimum, then the box
plot is positively skewed.
 Negatively Skewed: If the distance from the median to minimum is
greater than the distance from the median to the maximum, then the box
plot is negatively skewed.
 Symmetric: The box plot is said to be symmetric if the median is
equidistant from the maximum and minimum values.

12. steps in Making a Box-and-Whisker Plot
 Use the given data to make a box-and-whisker plot.
21, 25, 15, 13, 17, 19, 19, 21
Step 1.
Order the data from least to greatest. Then find the minimum, lower
quartile, median, upper quartile, and maximum.
minimum: 13 maximum: 25
lower quartile = = 16 Upper quartile = 21
Median: = 19

13. Step 2.
Draw a number line and plot a point above each value from
Step 1.

14. Step 3.
Draw the box and whiskers.

15. EXAMPLE 02
Use the given data to make a box-and-whisker plot.
31, 23, 33, 35, 26, 24, 31, 29
Step 1.
Order the data from least to greatest. Then find the minimum, lower
quartile, median, upper quartile, and maximum.
minimum: 23 maximum: 35
lower quartile: = 25 upper quartile: = 32
median: = 30

16. Step 2.
Draw a number line and plot a point above each
value.

17. Step 3.
Draw the box and whiskers.