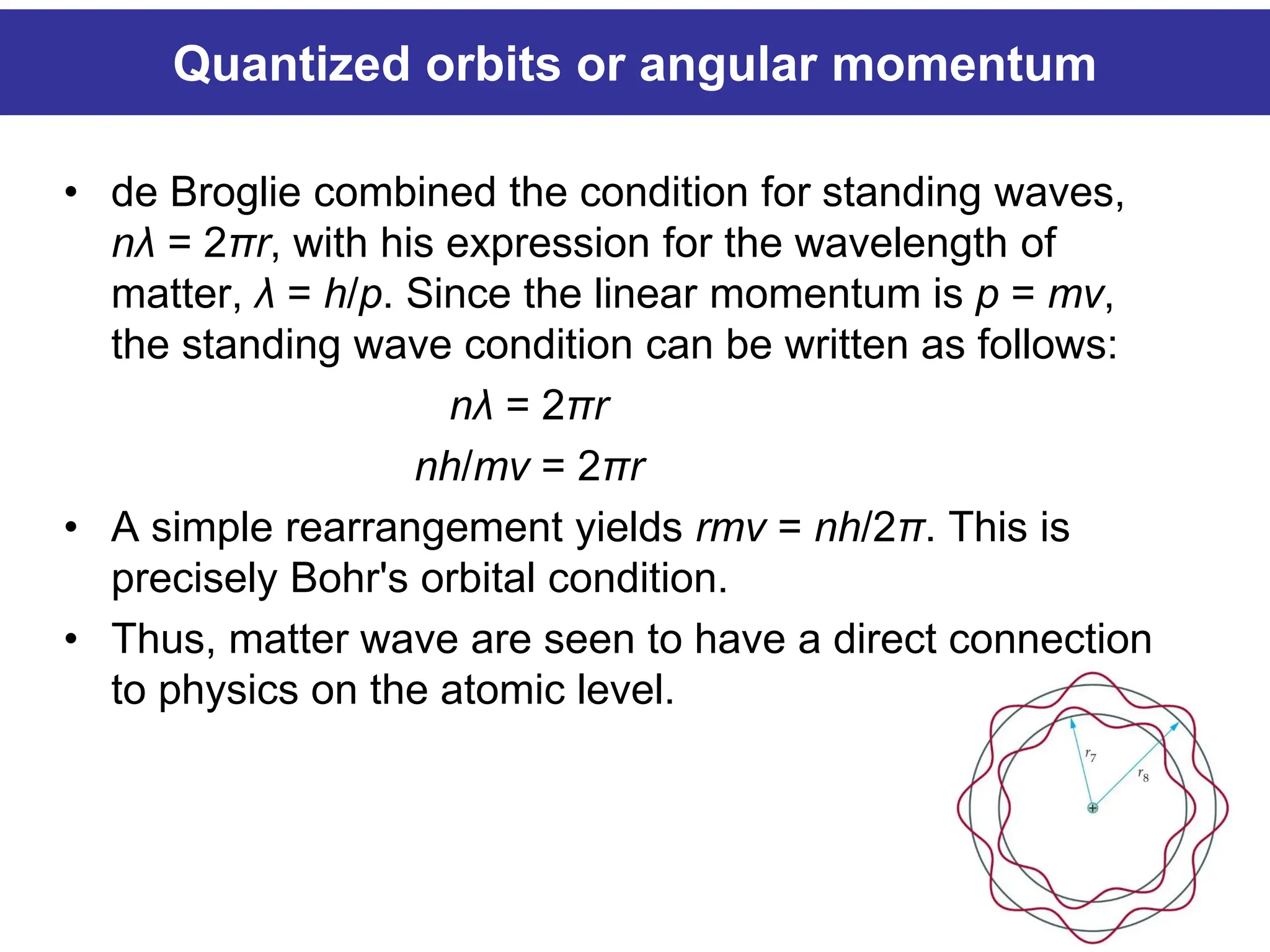
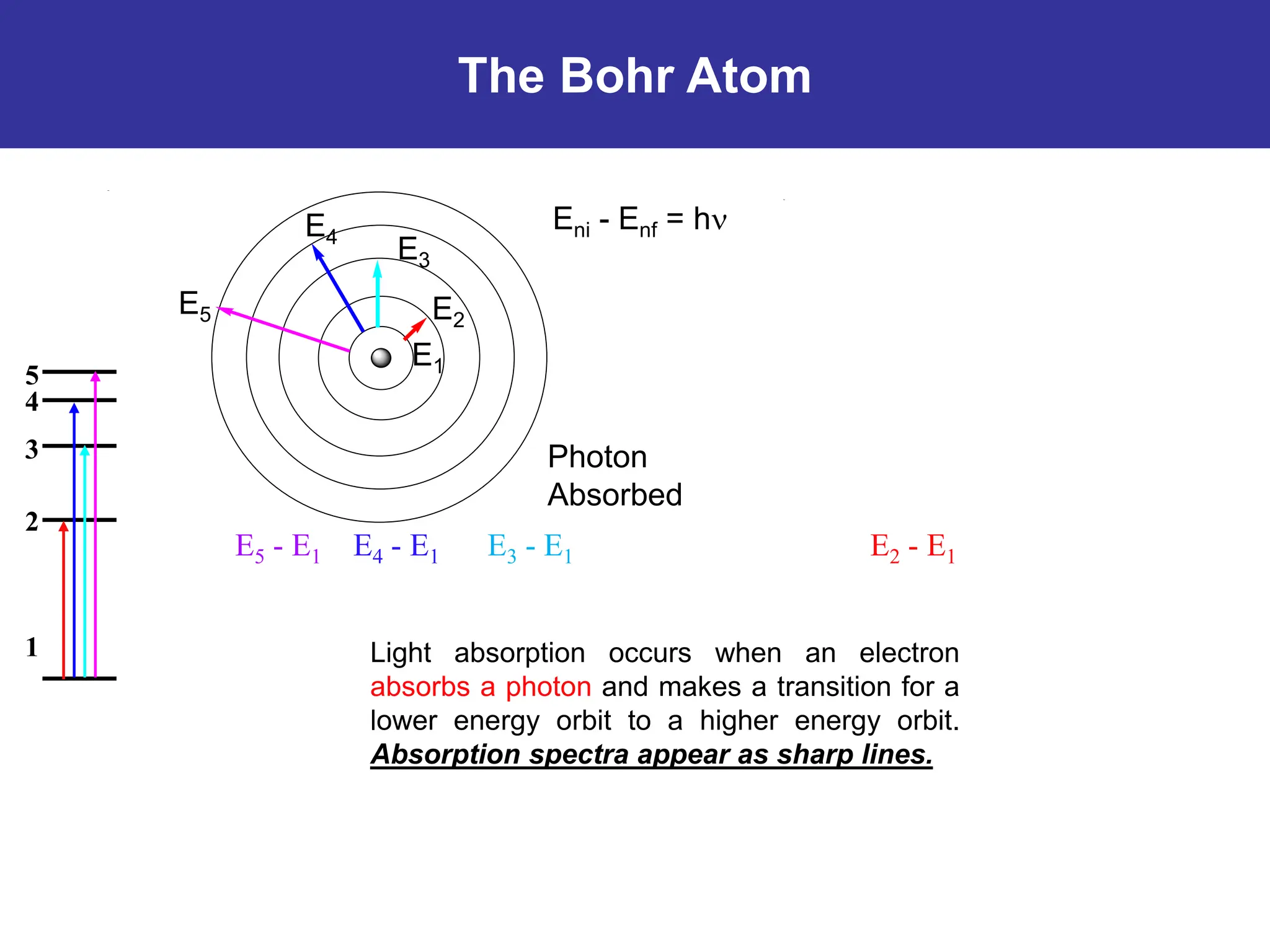
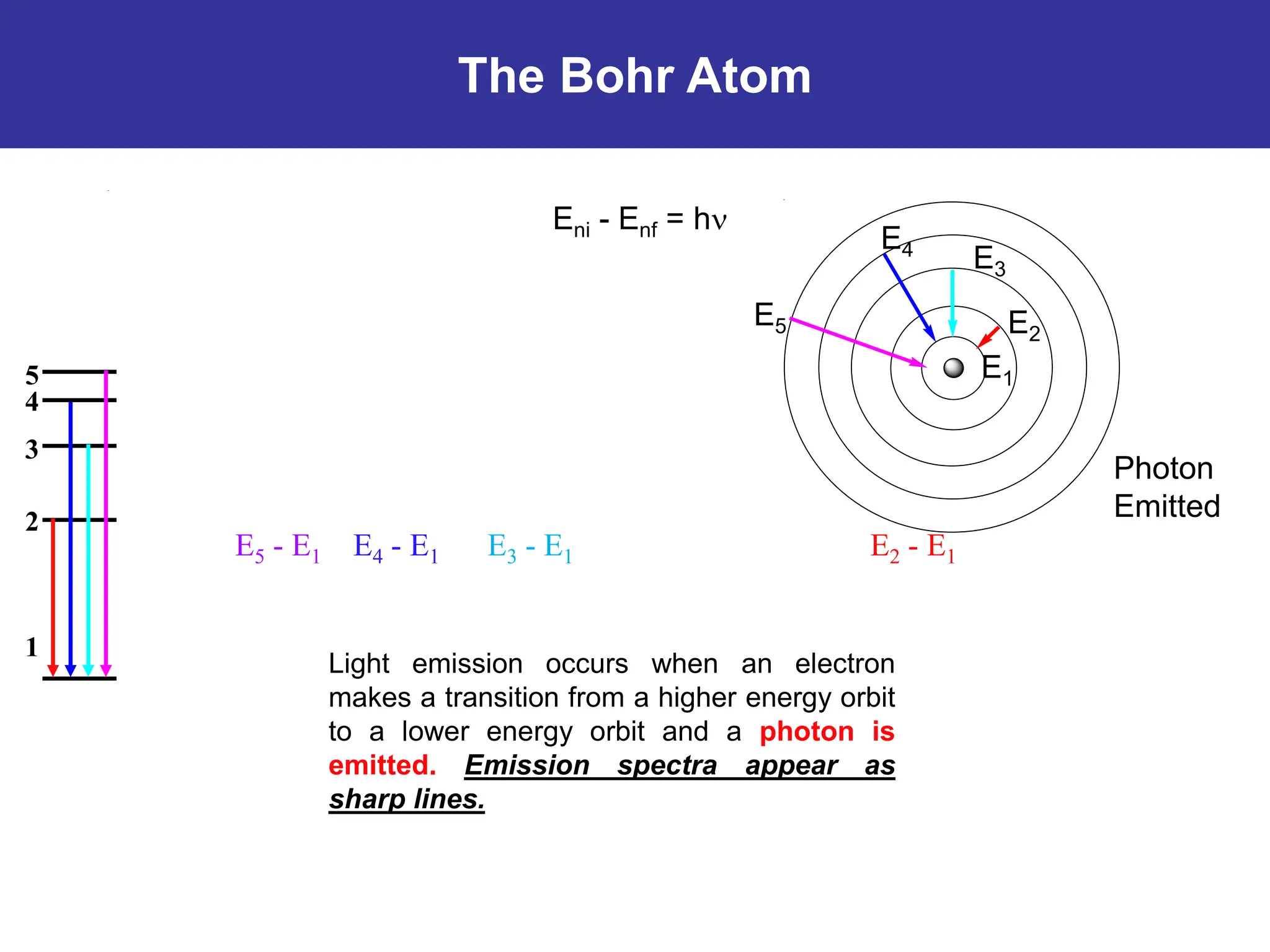
The Bohr atomic model describes that electrons in a hydrogen atom occupy specific quantized orbits characterized by fixed angular momentum. Energy is emitted or absorbed when electrons transition between these orbits, with the energy difference corresponding to emitted or absorbed light, which appears as sharp spectral lines. However, the model has limitations, particularly for atoms with more than one electron, and it cannot account for complex spectral structures or accurately represent electron behavior.